Метод социометрических измерений/Социометрическая матрица — Psylab.info
Материал Psylab.info — энциклопедии психодиагностики
Построение социометрической матрицы
По данным опроса испытуемых вначале составляется социометрическая матрица, по горизонтали и по вертикали которой в одном и том же порядке перечислены фамилии всех членов исследуемой группы. Нижние строки и крайние правые столбцы матрицы являются итоговыми. Заполнение матрицы начинается с внесения в нее выборов, сделанных каждым человеком. Для этого в клетках пересечения строки соответствующего испытуемого со столбцами тех, кого он выбрал, проставляются соответственно цифры 1, 2, 3. Цифра 1 ставится в столбец того члена группы, который рассматриваемым испытуемым оказался выбранным в первую очередь; цифра 2 – в столбце того члена группы, который был выбран вторым и т.д. Аналогичным образом, но цифрами другого цвета, в матрице отмечаются отклонения (тех, с кем не хотели в дальнейшем взаимодействовать). Обычно все данные, касающиеся положительных выборов, отмечают в матрице красным цветом, а отклонения – синим. В матрицу заносятся также результаты ответов на третий и четвертый вопросы; когда испытуемый предполагает, что его выберет кто-либо, то в столбец этого человека проставляются красные скобки, а скобками синего цвета отмечаются предполагаемые отклонения.
Социометрическая матрица
| Ф.И.О. | Иванов | Петров | Сидоров | … | ВС | ОС | ОВ | ОО |
|---|---|---|---|---|---|---|---|---|
| Иванов | 2 | ( ) | ||||||
| Петров | 1 | |||||||
| Сидоров | 3 | ( ) | 1 2 | |||||
| Обозначение показателей | ||||||||
| ВП | 2 | 1 | 0 | |||||
| ОП | ||||||||
| ОВ | ||||||||
| ОС | ||||||||
| ВВ | ||||||||
| ВО |
В итоговых нижних строках и правых столбцах используются следующие обозначения:
- ВС – количество выборов, сделанных данным человеком;
- ОС – количество отклонений, сделанных данным человеком;
- ВП – сумма выборов, полученных данным человеком;
- ОП – сумма отклонений, полученных данным человеком;
- ОВ – количество ожидаемых выборов;
- ОО – количество ожидаемых отклонений;
- ВВ – количество взаимных выборов;
- ВО – количество взаимных отклонений.
В нижние строки матрицы заносятся результаты о количестве полученных выборов (независимо, в какую очередь – 1, 2, 3-ю) и отклонений, о количестве взаимных выборов и отклонений, о количестве ожидаемых от данного лица выборов и отклонений.
В крайние правые столбцы матрицы заносятся результаты о количестве сделанных выборов и отклонений, о количестве ожидаемых данным лицом выборов и отклонений.
Число выборов, полученных каждым человеком, является мерилом положения его в системе личных отношений, измеряет его «социометрический статус». Люди, которые получают наибольшее количество выборов, пользуются наибольшей популярностью, симпатией, их именуют «звездами». Обычно к группе «звезд» по числу полученных выборов относят тех, кто получает 6 и более выборов (если, по условиям опыта каждый член группы делал 3 выбора). Если человек получает среднее число выборов, его относят к категории «предпочитаемых», если меньше среднего числа выборов (1-2 выбора), то к категории «пренебрегаемых», если не получил ни одного выбора, то к категории «изолированных», если получил только отклонения – то к категории «отвергаемых».
С целью более достоверного выделения «звезд» и «пренебрегаемых» используют некоторые методы статистического анализа. В ходе статистического анализа полученного первичного материала устанавливают критические значения количества выборов, границы доверительного интервала, за пределами которого полученные выборы можно считать статистически достоверными. Эмпирические кривые распределения выборов часто асимметричны и апроксимируются биноминальным законом распределения. Экспериментальная ситуация социометрического обследования весьма близка к ситуации последовательных дихотомических выборов.
Формулы расчёта
Верхняя и нижняя критические границы рассчитываются по следующей общей формуле:
[math]\mathbf{X}=\mathbf \bar{M}+{t \bar{b}}[/math]
где Х – критическое значение количества V(М) выборов;
t – поправочный коэффициент, учитывающий отклонение эмпирического распределения от теоретического;
b – среднее отклонение;
M – среднее количество выборов, приходящихся на одного человека.
Коэффициент t определяется по специальной таблице на основе предварительного вычисления другого коэффициента ОD свидетельствующего о степени отклонения распределения выборов от случайного:
[math]O_\text{D} = \frac{ \mathit{I} \bar{p} — \mathit{I} \bar{q}}{\bar{b}}[/math]
где p – оценка вероятности быть выбранным в данной группе;
q – оценка вероятности оказатьcя отвергнутым в данной группе;
b – отклонение количества полученных индивидами выборов от среднего их числа, приходящегося на одного члена группы;
p и q, в свою очередь, определяются при помощи следующих формул:
[math]\bar{p} = \frac{\mathbf \bar{M}}{(N-1)}[/math], [math]\bar{q} = {1 — \bar{p}}[/math]
где N – количество участников в группе;
M– среднее количество выборов, полученных одним участником.
M вычисляется при помощи формулы:
[math]\bar{M} = \sum_{i=1}^N \frac{d}{(N-1)}[/math]
где d – общее количество выборов, сделанных членами данной группы.
b определяется по формуле:
[math]\bar{b} = \sqrt{{(N-1)}{\cdot \bar{p}}{\cdot \bar{q}}}[/math]
Пример процедуры расчётов
Проиллюстрируем процедуру расчетов. Исследовали группу в 31 человек, участники которой в общей сложности сделали 270 выборов. Найдем среднее количество выборов, приходящихся на одного человека в группе:
[math]\bar{M} — \frac{270}{300} = 9,0[/math]
Определим оценку вероятности быть избранным в данной группе:
[math]\bar{p} = \frac{9,0}{30} = 30[/math]
Вычислим среднее квадратное отклонение:
[math]\bar{b} = \sqrt{{30}{\cdot 0,3}{\cdot (1 — 0,3)}} = 2,51 [/math]
Подсчитаем коэффициент асимметричности:
[math]O_\text{D} = \frac{ 0,7 — 0,3}{2,51} = 0,16[/math]
Теперь по таблице определим величину t отдельно для правой и левой частей распределения. В левой части таблицы приведены значения для нижней границы доверительного интервала, а в правой – для верхней. Для обеих границ (верхней и нижней) значения даны для трех различных вероятностей допустимой ошибки:
[math]p \le 0,05[/math]; [math]p \le 0,01[/math]; [math]p \le 0,001[/math];
Таблица значений коэффициента асимметричности по Сальвосу
| Коэффициент асимметричности ОD | Вероятность ошибки p | Коэффициент асимметричности ОD | Вероятность ошибки p | ||||
|---|---|---|---|---|---|---|---|
| 0,05 | 0,01 | 0,001 | 0,05 | 0,01 | 0,001 | ||
| 0,0 | -1,64 | -2,33 | -3,09 | 0,0 | 1,64 | 2,33 | 3,09 |
| 0,1 | -1,62 | -2,25 | -2,95 | 0,1 | 1,67 | 2,40 | 3,23 |
| 0,2 | -1,59 | -2,18 | -2,81 | 0,2 | 1,70 | 2,47 | 3,38 |
| 0,3 | -1,56 | -2,10 | -2,67 | 0,3 | 1,73 | 2,54 | 3,52 |
| 0,4 | -1,52 | -2,03 | -2,53 | 0,4 | 1,75 | 2,62 | 3,67 |
| 0,5 | -1,49 | -1,95 | -2,40 | 0,5 | 1,77 | 2,69 | 3,81 |
| 0,6 | -1,46 | -1,88 | -2,27 | 0,6 | 1,80 | 2,76 | 3,96 |
| 0,7 | -1,42 | -1,81 | -2,14 | 0,7 | 1,82 | 2,83 | 4,10 |
| 0,8 | -1,39 | -1,73 | -2,00 | 0,8 | 1,84 | 2,89 | 4,24 |
| 0,9 | -1,35 | -1,66 | -1,90 | 0,9 | 1,86 | 2,96 | 4,39 |
| 1,0 | -1,32 | -1,59 | -1,79 | 1,0 | 1,88 | 3,02 | 4,53 |
| 1,1 | -1,28 | -1,52 | -1,68 | 1,1 | 1,89 | 3,09 | 4,67 |
Поскольку в таблице нет значения, равного 0,16, а есть только значения 0,1 и 0,2, то выберем поправочные коэффициенты, находящиеся между этими табличными значениями.
Для ОD=0,1 поправочный коэффициент составит (-1,62), а для ОD=0,2 – (-1,59). С учетом того, что реальное значение ОD=0,16, возьмем поправочный коэффициент t промежуточного значения и примем его равным (-1,60) (левая половина таблицы).
Проделав подобную операцию и в правой части таблицы, получим второй поправочный коэффициент 1,69, величина которого расположена между табличными значениями для ОD=0,1 и ОD=0,2. Верхнюю критическую границу вычислим, подставив в формулу значение t из правой части таблицы: Xверхн = 9,0 + 1,69 х 2,51 = 13,24.
Для определения нижней границы доверительного интервала используем значение t, взятое из левой части таблицы: Хнижн = 9,0 – 1,6 x 2,51 = 4,98.
В связи с тем, что количество полученных выборов – это всегда целое число, округлим полученные значения до целых чисел.
Теперь можно сделать вывод, что все испытуемые изученной группы, получившие 14 и более выборов, имеют высокий социометрический статус, являются «звездами», а испытуемые, получившие 4 и меньше выборов, – низкий статус, причем, утверждая это, допускаем ошибку не более 5 %.
Если допускать ошибку в 1 %, то из таблицы значения t берем иные:
Xверхн = 9,0 + 3,32 х 2,51 = 17,33; Хнижн = 9,0 – 2,84 x 2,51 = 1,87.
Округлим до целых чисел: Xверхн = 18; Хнижн = 1. Таким образом, допуская ошибку не более, чем на 1 %, можно утверждать, что лидерами являются только те, кто получил не менее 18 выборов, а низкий статус – у испытуемых, получивших меньше двух выборов.
Анализ социоматрицы по каждому критерию дает достаточно наглядную картину взаимоотношений в группе. Могут быть построены суммарные социоматрицы, дающие картину выборов по нескольким критериям, а также социоматрицы по данным межгрупповых выборов.
Основное достоинство социоматрицы – возможность представить выборы в числовом виде, что в свою очередь позволяет проранжировать порядок влияний в группе. На основе социоматрицы строится социограмма – карта социометрических выборов (социометрическая карта), производится расчет социометрических индексов.
См. также
Социограмма | Социометрические индексы
Социометрическая матрица — Студопедия
Социоматрица — это матрица связей, с помощью которой анализируются внутриколлективные отношения. В социоматрицу в форме числовых значений и символов заносится информация, полученная в ходе опроса.
Анализ социоматрицы по каждому критерию дает достаточно наглядную картину взаимоотношений в группе. Могут быть построены суммарные социоматрицы, дающие картину выборов по нескольким критериям, а также социоматрицы по данным межгрупповых выборов.
Основное достоинство социоматрицы – возможность представить выборы в числовом виде, что в свою очередь позволяет проранжировать порядок влияний в группе. На основе социоматрицы строится социограмма – карта социометрических выборов (социометрическая карта), производится расчет социометрических индексов.
Подробнее о социометрической матрице
Социограмма
Социограмма – схематическое изображение реакции испытуемых друг на друга при ответах на социометрический критерий. Социограмма позволяет произвести сравнительный анализ структуры взаимоотношений в группе в пространстве на некоторой плоскости («щите») с помощью специальных знаков.
Социограммы бывают двух типов:
· групповые
· индивидуальные
Первые изображают картину взаимоотношений в группе в целом, вторые – систему отношений, существующих у интересующего исследователя индивида с остальными членами его группы.
Групповые социограммы в свою очередь могут быть представлены в виде:
· конвенциональной социограммы — индивиды, составляющие группу, изображаются в виде кружочков, соединенных между собой стрелками, символизирующими социометрические выборы или отклонения.
· «социограммы-мишени» — представляет собой систему концентрических окружностей, количество которых равно максимальному количеству выборов, полученных в группе. Все члены группы располагаются на окружностях в соответствии с количеством полученных выборов. Вся социограмма-мишень делится на секторы по социально-демографическим характеристикам группы (пол, возраст и т. п.).
Индивидуальные социограммы применяют для более наглядного представления о положении отдельных лиц в группе, на которых изображают индивида в совокупности всех его связей с другими членами группы.
Подробнее о социограммах
СОЦИОМЕТРИЧЕСКАЯ МАТРИЦА. — Студопедия
По данным опроса испытуемых вначале составляется социометрическая матрица, по горизонтали и по вертикали которой в одном и том же порядке перечислены фамилии всех членов исследуемой группы. Нижние строки и крайние правые столбцы матрицы являются итоговыми. Результаты выборов разносятся по матрице с помощью условных обозначений.
Заполнение матрицы начинается с внесения в нее выборов, сделанных каждым человеком. Для этого в клетках пересечения строки соответствующего испытуемого со столбцами тех, кого он выбрал, проставляются соответственно цифры 1, 2, 3. Цифра 1 ставится в столбец того члена группы, который рассматриваемым испытуемым оказался выбранным в первую очередь; цифра 2 – в столбце того члена группы, который был выбран вторым и т.д. Аналогичным образом, но цифрами другого цвета, в матрице отмечаются отклонения (тех, с кем не хотели в дальнейшем взаимодействовать). Обычно все данные, касающиеся положительных выборов, отмечают в матрице красным цветом, а отклонения – синим. В матрицу заносятся также результаты ответов на третий и четвертый вопросы; когда испытуемый предполагает, что его выберет кто-либо, то в столбец этого человека проставляются красные скобки, а скобками синего цвета отмечаются предполагаемые отклонения.
В нижние строки матрицы заносятся результатыо количестве полученных выборов (независимо, в какую очередь – 1, 2, 3-ю) и отклонений, о количестве взаимных выборов и отклонений, о количестве ожидаемых от данного лица выборов и отклонений.
В крайние правые столбцы матрицы заносятся результаты о количестве сделанных выборов и отклонений, о количестве ожидаемых данным лицом выборов и отклонений.
В итоговых нижних строках и правых столбцах используются следующие обозначения:
ВС – количество выборов, сделанных данным человеком;
ОС – количество отклонений, сделанных данным человеком;
ВП – сумма выборов, полученных данным человеком;
ОП – сумма отклонений, полученных данным человеком;
ОВ – количество ожидаемых выборов;
ОО – количество ожидаемых отклонений;
ВВ – количество взаимных выборов;
ВО – количество взаимных отклонений.
СОЦИОМЕТРИЧЕСКАЯ МАТРИЦА Ф.И.О. Иванов Петров Сидоров …
ВС ОС ОВ ОО Иванов 2 ( ) Петров 1 Сидоров 3 ( ) 1 2 Обозначение показателей ВП 2 1 0 ОП ОВ ОС ВВ ВО
Число выборов, полученных каждым человеком, является мерилом положения его в системе личных отношений, измеряет его«социометрический статус»:
«Звездами» именуют людей, которые получают наибольшее количество выборов, пользуются наибольшей популярностью, симпатией. Они обычно получают 6 и более выборов (если, по условиям опыта каждый член группы делал 3 выбора).
«Предпочитаемые» — те, кто получает среднее число выборов (3-5).
«Пренебрегаемые» — получают меньше среднего числа выборов (1-2).
Изолированные» — те, кто не получил ни одного выбора.
«Отвергаемые» — получают только отклонения.
СОЦИОГРАММА
–схематическое изображение реакции испытуемых друг на друга при ответах на социометрический критерий.
Социограмма позволяет произвести сравнительный анализ структуры взаимоотношений в группе в пространстве на некоторой плоскости («щите») с помощью специальных знаков. Она дает возможность более глубокого качественного описания и наглядного представления групповых явлений. Анализ социограммы начинается сотыскания центральных, наиболее влиятельных членов, затем взаимных пар и группировок.
Социограммы бывают двух типов:
1.Групповые–изображают картину взаимоотношений в группе в целом: группировкисоставляются из взаимосвязанных лиц, стремящихся выбирать друг друга.
Групповая социограмма имеет два варианта:
а) конвенциональная социограмма —индивиды, составляющие группу, изображаются в виде кружочков, соединенных между собой стрелками, символизирующими социометрические выборы или отклонения и располагаются по вертикали в соответствии с количеством полученных ими выборов таким образом, чтобы в верхней части социограммы оказались те, кто получил наибольшее количество выборов.
б) социограмма-мишень — представляет собой систему концентрических окружностей, количество которых равно максимальному количеству выборов, полученных в группе. Все члены группы располагаются на окружностях в соответствии с количеством полученных выборов. Она делится на секторы по социально-демографическим характеристикам группы (пол, возраст и т. п.).
2.Индивидуальные – отображают систему отношений, существующих у интересующего исследователя индивида с остальными членами его группы, в совокупности всех его связей.
Социометрическая карта-монограмма — дает социометрический срез группы в индивидуально-детализированном виде: изображает отношения каждого члена группы с остальными ее участниками.
Типичные социометрические связи:
1. Взаимные:
а) парные – когда индивид находится во взаимных отношениях не более чем с одним членом группы;
б) групповые – включающие взаимные выборы с двумя и более членами группы.
2. Односторонние:
а) изолированные – сам индивид выбирает других, а его не выбирает никто;
б) блуждающие – индивида выбирают одни члены группы, а сам он выбирает совершенно других;
в) обособленные – индивиду отдают предпочтение, а сам он никого не выбирает.
Социометрическая матрица
Слева
по вертикали и сверху по горизонтали в
социометрической матрице (таблица 1)
перечисляются фамилии членов исследуемой
группы в одном и том же порядке, например,
в алфавитном или под шифром с
соответствующими номерами. В строках
социометрической матрицы, где указаны
фамилии членов группы, цифрами от 1 и
выше каким-либо определенным цветом,
например — синим, отмечаются выборы,
сделанные данным членом группы.
Соответствующие цифры проставляется
в клетках пересечения (цифрами +1, +2, +3
обозначают тех, кого выбрал каждый
испытуемый в первую, вторую, третью
очередь, цифрами -1, -2, -3 — тех, кого
подопытный не избирает в первую, вторую
и третью очередь) его строки со столбцом,
где указана фамилия выбираемого им
человека.
Таблица 1.
Социоматрица
№ | Кто выбирает (j | Кого | Сделанные выборы | Всего | ||||||||
1 | 2 | 3 | 4 | 5 | 6 | + | – | |||||
1 | Иванов | +3 | +1 | +2 | – | .. | 3 | 1 | 4 | |||
2 | Петров | +1 | +2 | – | – | .. | 2 | 2 | 4 | |||
3 | Сидоров | +3 | +2 | .. | 2 | 0 | 2 | |||||
4 | Егоров | +3 | – | .. | 1 | 1 | 2 | |||||
5 | Савин | +3 | – | – | +1 | .. | 2 | 2 | 4 | |||
6 | …. | .. | .. | .. | .. | .. | .. | .. | .. | .. | ||
N | ….. | .. | .. | .. | .. | .. | .. | .. | .. | .. | ||
Полученные выборы | ∑ (+) | 4 | 2 | 2 | 2 | 0 | .. | 9 | ||||
∑ (– ) | 0 | 1 | 1 | 1 | 3 | .. | 7 | |||||
Всего | 4 | 3 | 3 | 3 | 3 | .. | 16 | |||||
Примечание: «+»
– положительный выбор; «–» –
отрицательный выбор.
Например, во
фрагменте социометрической матрицы
отмечены, выборы, сделанные Ивановым:
второй его выбор приходится на Егорова,
первый — на Сидорова, третий — на
Петрова. Точно так же, но цифрами другого
цвета, например, красного, отмечаются
сделанные отклонения. В том случае, если
выборы или отклонения являются взаимными,
то соответствующий факт отмечается в
социометрической матрице заключением
цифр в кружки того же самого цвета,
который характеризует выборы или
отклонения.
Взаимный положительный
или отрицательный выбор обводится в
таблице (независимо от очередности
выбора). После того, как положительные
и отрицательные выборы будут занесены
в таблицу, надо подсчитать по вертикали
алгебраическую сумму всех полученных
каждым членом группы выборов (сумма
выборов). Потом надо подсчитать сумму
баллов для каждого члена группы, учитывая
при этом, что выбор в первую очередь
равняется +3 баллам (-3), во вторую — +2
(-2), в третью — +1(-1). После этого
подсчитывается общая алгебраическая
сумма, которая и определяет статус в
группе.
Крайние правые
столбцы и нижние строки социометрической
матрицы являются итоговыми. В них
вносятся суммарные данные о количестве
выборов и отклонений, полученных и
сделанных каждым из членов группы.
Подсчетом количества синих цифр в строке
каждого члена группы устанавливается
число сделанных им выборов, и соответствующие
данные записываются в первый правый
столбец социометрической матрицы.
Сведения о сделанных отклонениях
получаются тем же путем, но за счет
определения количества красных цифр,
имеющихся в строке, относящейся к
соответствующему испытуемому. Эти
сведения заносятся во второй правый
столбец социометрической матрицы.
Для того, чтобы
определить сколько выборов получил
член группы, надо посчитать количество
синих цифр, имеющихся в столбце с фамилией
этого члена группы и результат записать
в первую нижнюю строку социометрической
матрицы. Аналогичным образом определяется
и отмечается в матрице во второй ее
нижней строке число полученных отклонений.
В заключение устанавливается общее
число всех выборов и всех отклонений,
сделанных членами данной группы, и эти
результаты вписываются в те клетки
социометрической матрицы, которые
расположены в правом нижнем ее углу (в
табл. они отмечены знаками математической
суммы).
Просматривая
нижние строки заполненной социометрической
матрицы, можно определить лидера в
данной группе. Им будет тот из ее членов,
который получил наибольшее число
выборов. По количеству отклонений можно
также определить того, кто вызывает к
себе наибольшие антипатии. На его долю
придется наибольшее число отклонений.
Анализ
социоматрицы по каждому критерию дает
достаточно наглядную картину
взаимоотношений в группе. Могут быть
построены суммарные социоматрицы,
дающие картину выборов по нескольким
критериям, а также социоматрицы по
данным межгрупповых выборов. Основное
достоинство социоматрицы — возможность
представить выборы в числовом виде, что
в свою очередь позволяет проранжировать
членов группы по числу полученных и
отданных выборов, установить порядок
влияний в группе. На основе социоматрицы
строится социограмма — карта
социометрических выборов (социометрическая
карта).
Социометрическая матрица результатов выборов — Студопедия
| Имена учеников | № | |||||||||||||||
| Маргарита В. | ||||||||||||||||
| Паша А. | ||||||||||||||||
| Таня Е. | ||||||||||||||||
| Алена Е. | ||||||||||||||||
| Ангелина Е. | ||||||||||||||||
| Влад Кул. | ||||||||||||||||
| Влад Кис. | ||||||||||||||||
| Вероника Н. | ||||||||||||||||
| Люда Р. | ||||||||||||||||
| Алена С. | ||||||||||||||||
| Паша П. | ||||||||||||||||
| Виталя П. | ||||||||||||||||
| Илья Я. | ||||||||||||||||
| Саша Ю. | ||||||||||||||||
| Вероника Я. | ||||||||||||||||
| Число полученных выборов | ||||||||||||||||
| Число взаимных выборов |
По данным социометрической матрицы к первой статусной группе «звезд» (С1) относятся: 1) Маргарита В.; 2) Алена Е.; 3) Ангелина Е.; 4) Влад Кисель; 5) Вероника Я..
К «предпочитаемым»: 1) Влад Кульгун; 2) Вероника Н.; 3) Паша Б..
К «пренебрегаемым»: 1) Паша А.; 2) Люда Р.; 3) Виталя П.; 4) Илья Я..
К «изолированным»: 1) Таня Е.; 2) Алена С.; 3) Саша Ю..
Дифференциация испытуемых по статусным группам позволяет определить диагностические индивидуальные и групповые показатели межличностных отношений учеников III — го класса:
Коэффициент благополучия отношений.
КБО = (С1 + С2)/n,
где С1 – количество «звезд»,
С2 – количество «предпочитаемых», а n – число учеников в классе.
КБО = 5 + 3 /15*100% = 50%
Коэффициент благополучия взаимоотношений (КБО = 0,5) исследуемого класса определяется как высокий.
Коэффициент оптимальности отношений.
КОО = (С2+ С3)/n,
где С2 – количество предпочитаемых в этих.
КОО = 3+3/15 = 0,4
Коэффициент «звездности».
КЗ = С1/n = 5/15 = 0,3
Коэффициент «изолированности».
КИ = С4/n,
где С4 – количество «изолированных» в группе.
КИ = 3/15 = 0,2
Коэффициент взаимности выборов вычисляется отношением суммы взаимных выборов в группе к сумме всех произведенных испытуемыми выборов.
КВ = SВВ/SВ.
В нашем исследовании КВ = 20/43*100% = 50%
Коэффициент взаимности выборов учеников III класса характеризуется как высокий.
Коэффициент осознанности.
КО = R0/Rx*100%,
где R0 – число оправдавшихся ожидаемых выборов,
а Rx – число ожидаемых выборов.
В нашем исследовании КО = 20/45*100% = 44,4%, следовательно, коэффициент осознанности невысок.
Результаты взаимоотношений можно представить графически в виде социограммы (см. приложение А).
Анализ статусной структуры, полученной по результатам социометрии, показывает, что выборы между учениками в классе распределяются неравномерно. В классе есть дети всех групп, то есть те, кто получил большее число выборов, — I группа, и те, кто имеет среднее количество выборов – II группа, и получившие 1 – 2 выбора – III группа, и ученики, не получившие ни одного выбора, — IV группа. По данным социометрии в исследуемом III классе в первую группу входит 2 человека, что составляет 13,3% от общего количества учеников в классе; вторая группа составляет 40% от общего количества учащихся; третья группа 26,7%; четвертая группа 20%.
Меньше всего школьников находятся в крайних I и IV группах. Наиболее многочисленны по количеству II и III группы.
В благоприятном положении находится около 53% учеников класса. В неблагоприятном положении оказались 46% учеников.
В качестве дополнительного метода исследования была использована методика «Что мне нравится в школе» (см. Приложение Б). По результатам исследования было выявлено, что 60% испытуемых на заданный вопрос нарисовали саму школу; 20% детей нарисовали спортивный зал; 13% детей — себя и друзей; 7% — себя и школу. Из этого следует, что только 13% детей со школой ассоциируют не только учебу, но и общение. Одним из критериев анализа исследования является игровая комната. В данном случае игровой комнатой является спортивный зал. Этот критерий предполагает какую-то игровую деятельность, в которой имеют место и межличностные отношения. Этот критерий был отмечен 20% детей.
Таким образом, нами были выявлены:
— важные диагностические показатели состояния общегрупповых процессов (социометрический статус каждого ребенка в группе, благоприятность отношений, коэффициент «звездности», «изолированности», коэффициент «взаимности»).
— важность общения и межличностных отношений детей в школе (с помощью проективного метода).
Заключение
Таким образом, в ходе нашего исследования были выделены следующие выводы:
Межличностные отношения имеют ряд форм, особенностей, которые реализуются в коллективе, группе людей, группе сверстников в процессе общения в зависимости от различных факторов влияющих на них.
Межличностные отношения сверстников младшего школьного возраста зависят от многих факторов, таких как успешность в учебе, взаимная симпатия, общность интересов, внешние жизненные обстоятельства, половые признаки. Эти все факторы влияют на выбор взаимоотношений ребенка со сверстниками и их значимость.
Существуют три круга общения, которые характеризуют систему личных отношений в классе (Я.Коломинский).
В основе развития взаимоотношений в группе лежит потребность в общении, и эта потребность изменяется с возрастом. Она удовлетворяется разными детьми неодинаково.
Каждый член группы занимает особое положение и в системе личных и в системе деловых отношений, на которых влияют успехи ребенка, его личные предпочтения, его интересы, речевая культура, а конце III-IV класса и индивидуальные нравственные качества.
Положение ученика зависит от взаимных выборов, основанных на симпатиях, качеств личности и общественного мнения.
Коллектив может влиять на индивидуальное развитие личности только тогда, когда положение ребенка в системе межличностных отношений благополучно.
Дети занимают различное положение в системе личных взаимоотношений, не у всех есть эмоциональное благополучие.
То или иное положение ребенка в системе личных взаимоотношений не только зависит от определенных качеств его личности, но, в свою очередь, способствует выработке этих качеств.
Определив положение каждого ребенка в группе и его социометрический статус можно проанализировать структуру межличностных отношений в этой группе.
При помощи соответствующих методов и следования основным методологическим принципам мы подтвердили гипотезу исследования межличностных отношений в группе сверстников младшего школьного возраста, о том, что положение в системе межличностных отношений или социальный статус каждого ребенка, входящего в группу сверстников, определяет особенности этих отношений.
Список использованной литературы
Чеховских, М.И. Психология: учеб. пособие / М.И. Чеховских. – М.: Новое знание, 2003. – 380 с.
Маркс, Энгельс Ф. Соч. – 2-е изд. – Т.3 – 360 с.
Венгер, Л.А., Мухина, В.С. Психология: учеб. пособие для учащихся пед. училищ по специальностям «Дошк. Воспитание» и «Воспитание в дошк. учреждениях» / Л.А. Венгер, В.С. Мухина. — М.: Просвещение, 1988 – 336 с.
Коломинский, Я.Л. Социальная психология школьного класса: научно-метод. Пособие для педагогов и психологов / Я.Л. Коломинский. – Минск: ООО «ФУА информ», 2003 – 312 с.
Немов, Р.С. Психология: учеб. пособие для студентов высших пед. учеб. заведений : В 3 кн. – 4-е изд. / Р.С. Немов.– М.: Гуманитарный издательский центр ВЛАДОС, 2001. – Кн.1. Общие основы психологии – 688 с.
Столяренко, Л.Д. Основы психологии: учеб. пособие для студентов высш. пед. заведений. / Л.Д. Столяренко. – Ростов н/Д. Издательство «Феникс», 1997 – 736 с.
Грейс Крайг. Психология развития / Грейс Крайг. – Серия «Мастера психологии», 2002. – 992 с.
Дубровина, И.В., Данилова, Е.Е., Прихожан, А.М. Психология./ Под ред. И. В. Дубровиной. – М.: Просвещение, 1999. – 464 с.
Возрастная и педагогическая психология: учебное пособие для студентов пед. институтов по спец. №2121 «Педагогика и методика начального обучения» / М.В. Матюхина, Т.С. Михальчик, Н.Ф. Прокина [и др.], под общей ред.М.В. Гамезо. – М.: Просвещение, 1984. – 256 с.
Раттер М. Помощь трудным детям. / Раттер Р. –М.: Просвещение, 1987.- 325 с.
Психология развития: учебник для студентов высш. пед. и психол. учеб. заведений / Г.М. Марютина, Т.Г. Стефаненко, К.Н. Поливанова [и др.], под ред. Т.Д. Марцинковской. – М.: Издательский центр «Академия», 2001. – 352 с.
Сапагова, Е.Е. Психология развития человека: учебное пособие / Е.Е. Сапагова. – М.: Аспект пресс, 2001. – 460 с.
Реан, А.А., Коломинский, Я.Л. Социально-педагогическая психология / А.А. Реан, Я.Л. Коломинский. – Серия «Мастера психологии» – Питер, С – Птб, 2000. – 212 с.
Волков, Б.С., Волкова Возрастная психология. В 2-х частях. Ч.2: От младшего школьного возраста до юношества: учебное пособие для студентов вузов, обучающихся по пед. специальностям / Б.С. Волков, Н.В. Волкова, под ред. Б.С.Волкова. – М.: Гуманитарный издательский центр ВЛАДОС, 2005. – 343 с.
Психология человека от рождения до смерти / Под ред. А.А. Реана. – СПб: Питер, 2002. – 544 с.
Мухина, В.С. Возрастная психология: феноменология развития, детство, отрочество: учебник для студентов вузов: 4-е изд., стереотип / В.С. Мухина. – М.: Издательский центр «Академия», 1999. – 456 с.
Киричук, А.В. Проблемы общения и воспитания / А.В. Киричук. – ч. 2 – Тарту, 1974. – 375 с.
Крутецкий, В.А. Психология: учебник для учащихся пед. училищ / В.А. Крутецкий. – 2-е изд., перераб. и доп. – М.: Просвещение, 1986. – 336 с.
Божович, Л.И. Личность и ее формирование в детском возрасте / Л.И. Божович. – М.: Педагогика, 1968. – 296 с.
Амельков, А.А. Психологическая диагностика межличностного взаимодействия / А.А. Амельков. – Мозырь: Содействие, 2006. – 108 с.
Приложение Б
Проективная методика
«Что мне нравится в школе»
(Н.Г. Лусканова)
Назначение: методика выявляет межличностные отношения детей в группе сверстников младшего школьного возраста.
Инструкция: «Дети, нарисуйте то, что вам больше нравится в школе. Рисовать можно все, что хотите. Рисуйте, как сможете, оценки за рисунки ставиться не будут».
Интерпретация:
несоответствие указанной теме;
преобладание других мотивов, например учебы;
детский негативизм. Ребенок отказывается рисовать данную тему, а рисует то, что он умеет и то, что ему больше нравится;
дети часто рисуют игры, игровую комнату, игрушки;
дети часто рисуют детей.
Существуют и многие другие интерпретации данной методики.
Страницы: 1 2
Похожие рефераты:
Взоимодействие тревожности и социометрического статуса в младшем школьном возрасте
Особенности тревожности и социометрического статуса у младших школьников. Организация эмпирического исследования взаимосвязи уровня тревожности и социометрического статуса (личностные особенности младшего школьника и статусное положение ребенка в классе).
Изучение межличностных отношений в детском объединении
Межличностные отношения — показатель психологического климата коллектива и успешности деятельности. Формирование психологического климата. Социометрическое исследование положения детей в системе межличностных отношений коллектива школьного объединения.
Характеристика младшего школьного возраста
Интересы и ценности ребенка младшего школьного возраста. Кризис 7 лет и изменение самосознания ребенка, его личности и психических функций: половая идентификация, психологическое время личности, развитие чувств. Воспитание младшего школьника в играх.
Психология детей начальных классов
Возможности развития эмоциональной сферы младших школьников. Адаптационный период ребенка-первоклассника. Динамика школьных страхов на начальной ступени обучения. Поступление в школу и период адаптации. Характеристика личностного развития первоклассников.
Психические особенности общения младших школьников
Характеристика понятия, функций, видов общения. Особенности формировании человека, как личности, объекта и субъекта общения. Стили педагогического общения и их технологическая характеристика. Психические особенности общения в младшем школьном возрасте.
Изучение отношений и предпочтений в классном коллективе
Анализ проблемы отношений и предпочтений в классном коллективе. Межличностные отношения и отношение к совместной деятельности. Описание исследования предпочтений и отношений в классном коллективе. Методические основы исследования, контингент испытуемых.
Общение младших школьников
Особенности межличностных отношений и общения младших школьников. Упражнения на развитие умений общения у младших школьников. Эмоционально-смысловые доминанты общения детского типа: познание, деятельность и игра. Аспекты общения школьников со взрослыми.
Особенности межличностного общения детей младшего школьного возраста с разным уровнем академической успеваемости
Понятие межличностных отношений в коллективах. Развитие межличностных отношений детей младшего школьного возраста. Успеваемость школьного обучения как психолого-педагогическая проблема. Соотношение академической успеваемости и межличностных отношений.
Диагностика межличностных отношений в классе
Отношения между учениками в классе. Прогноз реакции друг на друга. Общая социально-психологическая характеристика класса. Психологическая структура школьного класса. Возрастные аспекты социально-психологической структуры класса.
Самооценка учащегося и уровень его притязаний
Анализ взаимосвязи самооценки и уровня притязаний. Особенности личностного развития младшего школьника, показателей его самооценки и уровня притязаний. Профилактическая и коррекционная работа с детьми, имеющими отклонения в уровне самооценки и притязаний.
Особенности межличностного общения в подростковом возрасте
Для подросткового возраста характерно создание собственного мнения на основе сравнения своего мнения с мнениями сверстников. Ценным для подростка является вовлеченность в сам процесс общения. Подросток реализует себя как личность, формирует суждения о себ
Социометрическое тестирование
Методика проведения социометрического опроса как разновидности опроса для определения взаимоотношений между членами коллектива, положения в нем отдельных членов путем взаимовыборов по предложенным критериям. Социометрическая матрица (социограмма).
Формирование коллектива учащихся класса интегрированного обучения
Понятия интегрированного обучения и ученического коллектива. Формирование коллектива учащихся как условие эффективности интегрированного обучения. Изучение межличностных отношений учащихся класса. Рекомендации по формированию положительных отношений.
Особенности межличностных отношений младших школьников в классах с развивающим и традиционным обучением
Системы развивающего обучения. Сравнительный анализ принципов традиционного и развивающего обучения, являющихся основой формирования межличностных отношений детей младшего школьного возраста. Метод социометрических измерений. Методика срезов Т.А.Репиной.
Психологическая характеристика коллектива
Межличностные отношения в коллективе. Групповые процессы в коллективе.
Психологический портрет младших школьников с различным статусом в социометрической иерархии
Психологическая характеристика учеников младшего школьного возраста. Генезис взаимоотношений детей младшего школьного возраста со сверстниками. Ребенок младшего школьного возраста в системе социальных отношений. Особенности и структура учебной группы.
Межличностные отношения детей подросткового возраста
Исследование межличностных отношений в работах психологов. Особенности межличностных отношений подростков. Психологический климат группы. Влияние стиля педагогического общения на межличностные отношения подростков. Организация и методика исследования.
Проблемы взаимоотношений подростков
Характеристика взаимоотношений подростков. Потребность в общении как фактор развития взаимоотношений. Особенности взаимоотношений подростков в школьном коллективе. Общение со сверстниками: любовь, дружба. Проблемы взаимоотношений детей со взрослыми.
Влияние коммуникативных качеств подростка на социометрический статус в группе
Психологические особенности подросткового возраста. Межличностные отношения подростков в группе, их специфические черты. Исследование взаимосвязи личностных качеств и положения подростков в группе, формирование и интерпретация полученных результатов.
Ведущая деятельность и новообразования в младшем школьном возрасте
Характеристика учебной деятельности-ведущая в младшем школьном возрасте, содержание, структура. Психологические новообразования познавательной сферы младшего школьника. Психологические новообразования личности и поведения в младшем школьном возрасте.
Социометрия. Теория и практика — Школа практической психологии Елены Могилевской
Бывают групповые и персональные индексы.
Персональные социометрические индексы.
Статус — обозначает место индивида системе жизнедеятельности группы, в развитии групповых процессов. Статус является ведущей функцией члена группы, его обязанностями перед ней. Он одновременно интегрирует в себе черты объективно присущие индивиду и то, как воспринимается окружающими исполнение им своих функций. Социометрический статус отражает отношение членов группы к каждому ее представителю.
Количество полученных i-членом выборов
S = ————————————————————
( N – 1)
где N – численность группы.
Имеет смысл вычислять положительные и отрицательные статусы являющиеся составными частями общего статуса индивида.
Количество полученных положительных выборов
S + = ———————————————————————
( N –1)
аналогично для S -.
Индекс эмоциональной экспансивности – характеризует то, насколько член группы связан с остальным членам, сколь активен он в своих выборах.
Количество выборов отданных i-членом группы
Е = ————————————————————————
( N -1 )
Аналогично вышеописанному выводятся индексы положительной и отрицательной экспансивности.
Групповые индексы.
N в
С = —————
N (N -1)
где С — эмоциональная сплоченность группы; Nв — количество взаимных выборов в группе; N (N -1) — общее возможное число взаимных выборов в группе.
Индекс групповой сплоченности не является показателем содержательного качества коллектива, т.к. степень сплоченности может быть высокой и в бандитской шайке и в уличной группировке. Однако, он всегда показывает насколько группа склонна к разрыву, распаду.
Индекс социометрической когерентности – характеризует меру связанности группы по выделенному критерию, настоятельность взаимных контактов, но без учета их знака и направленности.
Количество отданных ( или полученных )выборов
К= ——————————————————————-
N ( N – 1 )
Из формулы понятно, что, «К» является средним арифметическим социометрического статуса и эмоциональной экспансивности.
Индекс взаимности – измеряет сплоченность группы, проявляющуюся в количестве взаимных положительных связей.
Количество взаимных положительных выборов
G = —————————————————————-
N (N – 1 )
Социометрический индекс референтности
Количество взаимных положительных выборов
R = ———————————————————————
Количество положительных выборов.
Показывает насколько группа является референтной для каждого участника.
Классический социометрический тест, как и любая социометрическая процедура, после проведения, предполагает анализ мотивов, выборов, и отвержений, возможных причин и определение путей изменения неблагоприятных социометрических конфигураций.
Однако для нас важно понимать, что все эти индексы, по сути, характеризуют лишь различные аспекты таких комплексных проявлений человеческого взаимодействия как притяжение или отталкивание.
Социограмма
Социограмма — это графическое изображение динамической эмоциональной глубинной структуры группы. Вначале участники тестирования графически изображаются на бумаге с помощью символов, женщины в виде кружочков, мужчины в виде треугольников. Далее в соответствующем кружке или треугольнике указывается имя или присвоенный номер. Затем красными или сплошными линиями отмечаются все исходящие от конкретного индивида выборы, все отвержения изображаются соответственно черными или пунктирными линиями. Взаимные выборы или отвержения (так называемые пары взаимного притяжения или отталкивания) изображаются соответствующими соединительными линиями с поперечной чертой посередине. Интенсивность выбора, каким он был сделан: первым, вторым и т.д. указывают цифрой рядом с линией. Существует множество видов социограмм. Простейшей из них является круговая. В этом случае все члены группы располагаются симметрично на окружности и соответствующими линиями обозначаются связи между ними. Иногда для упрощения чертежа отдельно представляют положительные и отрицательные связи.
Социограммы локограмного вида заранее располагают на плоскости членов группы так, чтобы это расположение моделировало их действительное местоположение в том помещении, где происходит основная деятельность группы (класс, цех, офис)
После графического изображения результатов социометрического теста в социограмме, приступают к его качественной оценке. Существуют следующие позиции членов группы: Звезды притяжения, предпочитаемые члены группы, пренебрегаемые, изолированные, звезды отвержения или отвергаемые члены группы. Если, например, каждый член группы мог получить по три выбора то тот, кто получил 6 и более положительных – имеет статус «звезды», 3-5 – предпочитаемые, 1-2 – пренебрегаемые, 0 – изолированные, только отрицательные выборы – отвергаемые.
“Звезда притяжения”- человек, которого выбирает максимальное число участников группы, лидеры, оказывающие большое влияние на каждого участника и всю группы в целом .
“Звезды отвержения” — наиболее часто отвергаемые члены группы, так называемые “козлы отпущения”, наиболее уязвимые позиции в структуре группы. Данные позиции удобно анализировать с помощью еще одного вида социограммы — дифференциальной или концентрической социограммы, где все члены группы располагаются на концентрических окружностях и чем выше положительный статус члена группы, тем ближе к центру он помещается и наоборот.
Несколько менее известна следующая интерпретация групповых позиций, учитывающая наличие в группе нескольких центров притяжения:
-“альфа” — тот человек в группе, который содержит в себе наиболее важную позитивную энергию группы, а так же тот, кто тайно или явно держит в руках все нити власти и имеет наибольшее влияние. Именно альфа чаще всего является протагонистом, именно его темы интересуют большее количество участников группы.
-“бета” — антогонист “альфы”, является или экспертом или противником, отрицающим все идеи “альфы”. Он так же имеет определенное количество стронников но несколько меньшее чем «альфа». Темы выносимые «бетой» составляют конкуренцию «альфе» они часто меняются местами, что и создает основу групповой динамики.
-“гамма” — те люди, которые идут за “альфа” и все время поддерживают его.
-“омега” — “гадкий утенок”, в этой роли человек является носителем всего нежелательного, бессознательно отвергаемого группой. Некий канал утилизации групповых страхов. Обращение к темам «омеги» приводит к изменению всей групповой структуры и вызывает значительный рост самосознания в группе и групповой зрелости.
Эмпирически, на группу в 30 человек почти всегда приходится звезд 3-4, предпочитаемых 10 –12, пренебрегаемых — 10 –12, изолированных до 5 человек, причем изолированные не объединяются в подгруппу а остаются изолированными. Данные факты не являются случайными и объясняются сформулированным Морено социодинамическим законом: Неравномерное распределение выборов в социометрическом тестировании не устраняется при повышении шансов каждого участника быть выбранным. При повторном тестировании с большими возможностями для выбора оно становится еще более выраженным. Дополнительные выборы приходятся не на тех индивидов, которые редко выбираются или которые оказались в изоляции, а опять таки на звезд притяжения.
Анализ социограммы происходит с отыскания центральных, наиболее влиятельных членов, затем взаимных пар и группировок. Группировки составляются из взаимосвязанных лиц, стремящихся выбирать друг друга. Как правило, неформальных структур в группе возникает несколько: структуры взаимоподдержки, взаимовлияния, популярности, престижа, лидерства и др. Наиболее часто в социометрических измерениях встречаются группировки из 2, 3 членов реже из 4 и более членов. Группировки выполняют роль эмоциональных ядер общения. Их наличие или отсутствие характеризует психологический климат группы. В хорошо организованных, сплоченных группах лидеры группировок положительно взаимосвязаны, что находит отражение на социограмме.
пример:
см рис.
На одном небольшом предприятии, несмотря на благоприятные условия труда, существуют такие напряженные отношения между людьми, что из-за них страдает не только работа и процесс производства, но и сами работники. Некоторые из них вынуждены регулярно обращаться к врачу из-за психогенных недугов таких как головные и желудочные боли, расстройства сна и пр. Симптоматическое лечение, тем не менее, не приводит к цели если напряженность на предприятии остается скрытой и никто не знает в чем корень зла. Скрытой же она остается до тех пор, пока измеряется только внешняя структура, включающая руководителей двух подразделений (а и б), которые вместе с несколькими сотрудниками и секретаршами работают над различными проектами. Наряду с этим может быть исследована глубинная эмоциональная структура группы и расхождение между ними.
Как же применяется социометрический тест к группе, где возникли подобные нарушения?
В ходе тестирования членам упомянутого предприятия указывается на их проблемы и на важность знания выявляемых с помощью теста их выборов и отвержений для улучшения ситуации. В данном случае критерием теста является вопрос “ С кем из коллег из обоих подразделений вы хотели бы вместе работать, а с кем нет?” Каждый участник получает две карточки. На одной из них он указывает до пяти коллег, с которыми он хотел бы работать, а на другой тех с кем не хотел бы. Выполнив задание, участники тестирования сдают карточки с разным количеством выборов и отвержений социотерапевту. Так как социометрические выборы и отвержения зависят от критерия теста то для обстоятельного социометрического исследования должно быть проведено не менее двух социометрических тестов. На втором этапе исследования служащие определяются, с кем из коллег они хотелись бы сойтись поближе во время запланированной на предприятии совместной поездки на выходные. Обработку данных социометрических тестов можно провести не только с помощью математической обработки, но и на социограмме где данные структуры будут представлены максимально наглядно. Если мы исследуем социограммы 1 и 2 нашего примера ( небольшое предприятие с.
подразделениями а и б, то мы увидим одних и тех же участников но совершенно разные социометрические структуры
Тестовый критерий 1 относится к совместной работе. Данная социограмма указывает на расслоение подразделения а) на две подгруппы. Его шеф (1) в первом выборе отдает предпочтение руководителю второго подразделения (А), во втором и третьем выборах секретаршам (2) и (3). Обе сотрудницы отвергают друг друга.
Вторая подгруппа данного подразделения предстает в виде гармоничной закрытой структуры. Два сотрудника (4) и ( 7 ) выбирают друг друга, так как (7) в первом выборе выбирает секретаршу (6) , а (4) в первом выборе выбирает (7) , можно предположить, что именно (7) задает тон в этой конфигурации. Из первого выбора сотрудницы (5) можно увидеть, что она предпочла бы работать в параллельном подразделении. Ее слабовыраженное желание работать с коллегой (4) последним отвергается. Также и (7) отвергает (5) как сотрудницу. Никто не выразил желания с ней работать.
Необходимо также отметить крайне тяжелое в профессиональном отношении положение руководителей обоих подразделений, которые поддерживаются только взаимными выборами
Тестовый критерий 2 относится к совместному проведению досуга. Структурный анализ второй социограммы кардинально отличается от первой. Если в первой (5) только отвергается то во второй на веселую, молодую женщину приходиться 7 выборов, которые делают ее “звездой притяжения”. И наоборот (6) на этот раз оказывается полностью изолированной.
Групповая сплоченность подразделения б) по критерию сотрудничества с тремя внешними выборами лишь не намного меньше, чем сплоченность подразделения а). Отношение составляет 3:2. По второму критерию оно составляет вместе с отвержениями 7:1. Кроме того, на социограмме 2б) меньше парных, треугольных, цепных структур и нет фигуры звезды в качестве ключевой персоны. Структура подразделения б) по второму критерию является экстравертированной и характеризуется низкой сплоченностью.
Учащиеся 2б класса | Социометрическая матрица выбора/ Кого выбирают | ||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | |
1. Антипенков Данил | |||||||||||||||||||||||||||||
2. Березикова Анaстасия | |||||||||||||||||||||||||||||
3. Бирюкова Вeроника | |||||||||||||||||||||||||||||
4. Божко Арина | |||||||||||||||||||||||||||||
5. Бойко Алёнa | |||||||||||||||||||||||||||||
6. Бородина Софья | |||||||||||||||||||||||||||||
7. Бубенина София | |||||||||||||||||||||||||||||
8. Вихарев Илья | |||||||||||||||||||||||||||||
9. Ворожцов Мaксим | |||||||||||||||||||||||||||||
10. Зиннер Никитa | |||||||||||||||||||||||||||||
11. Кошкина Ксения | |||||||||||||||||||||||||||||
12. Малышева Ксения | |||||||||||||||||||||||||||||
13. Молчанова Надежда | |||||||||||||||||||||||||||||
14. Осадчев Владислав | |||||||||||||||||||||||||||||
15. Подколзин Никита | |||||||||||||||||||||||||||||
16. Попова Софья | |||||||||||||||||||||||||||||
17. Сапсай Арина | |||||||||||||||||||||||||||||
18. Сенцов Сергей | |||||||||||||||||||||||||||||
19. Силин Степан | |||||||||||||||||||||||||||||
20. Скрипкина Екатерина | |||||||||||||||||||||||||||||
21. Стоякин Данил | |||||||||||||||||||||||||||||
22. Сухова Виталина | |||||||||||||||||||||||||||||
23. Схоменко Дарина | |||||||||||||||||||||||||||||
24. Сычёв Александр | |||||||||||||||||||||||||||||
25. Тихонова Алёна | |||||||||||||||||||||||||||||
26. Чарикова Кристина | |||||||||||||||||||||||||||||
27. Чуб Евгений | |||||||||||||||||||||||||||||
28. Шумилова Елизавета | |||||||||||||||||||||||||||||
29. Яковлев Илья | |||||||||||||||||||||||||||||
Количество полученных выборов | |||||||||||||||||||||||||||||
Количество взаимных выборов | |||||||||||||||||||||||||||||
Количество невыборов | |||||||||||||||||||||||||||||
Социометрический матричный анализ ne demek Социометрический матричный анализ türkçesi ne demek ingilizce Социометрический матричный анализ anlamı
Bu sayfada ingilizce Социометрический матричный анализ türkçesi nedir Социометрический матричный анализ ne demek Социометрический матричный анализ ile ilgili cümleçi матричный анализ anlamı tanımı türkçe sözlük anlamı veya kelime anlamlarını bulabilirsiniz.
Социометрический матричный анализ türkçesi Социометрический матричный анализ nedir
- eşitli kümesel göstereçleri saptayabilmek üzere kümeölçüm ölçeriyle elde edilen çekim ve itimlerin birlikte dağılımını veren çizelgenin çözümlenmesi.
- Kümeölçüm çapraz çözümlemesi.
Социометрический матричный анализ ingilizcede ne demek, Социометрический матричный анализ nerede nasıl kullanılır?
Социометрический : Сосиометрик. Sosyal gruplar içindeki davranış ве ilişkilerin incelenmesi ve ölçümü ile ilgili. Sosyometri ile ilgili.
Матрица : Матрица. Bağ dokusunun (öz bağ, kemik, kıkırdak) су, минерал maddeler, glikozaminoglikanlar ве протеогликанлар gibi maddelerden oluşan zemin maddesi.kloroplastlarda zarların içinde kalan zemin maddesi. стромы. 3.mitokondrilerde iç zarın çevrelediği zemin maddesi. Каеды. Dikdörtgen biçiminde yatık, dik sıralardan yapılmış iki boyutlu sayılar dizisi. Кемик dokuda bulunan hücre içi madde. kendisinden kıl, tırnak, bazal zar veya hücre iskeleti gibi yapı veya unsurların şekillendiği dokuların genel adı. döl yatağı. бир неснее бичим верен вейа дайанак олан шей. Бир Хюкре Вея Органелин Джел Киваминдаки Сыви Ичериги. Uzbilimsel öğelerin cebirsel kurallara uygun olarak dizi ve dikeçler biçiminde düzenlenmesi.Матрикс. Рахим. Bilgisayar, biyoloji, fizik, kimya, sinema, televizyon, veterinerlik alanlarında kullanılır. Dölyatağı.
Анализ : İnceleme, irdeleme. Çözüm. Analiz etme. İnceleme. Çözümleme. Анализ. Bilgisayar, bilişim, eğitim, fizik, gümrük, kimya, madencilik, ekonomi, sosyoloji, veterinerlik alanlarında kullanılır. Тахлил. Мал niteliğinin anlaşılması için, gerektiğinde о мал я да örneği üzerinde yapılan kimyasal işlem. Sayışım dökümü.
,
Рассечение матрицы камеры, Часть 3: Внутренняя матрица ←
13 августа 2013 г.

Сегодня мы изучим внутреннюю матрицу камеры в нашей третьей и последней главе трилогии «Рассечение матрицы камеры». В первой статье мы узнали, как разделить полную матрицу камеры на внутреннюю и внешнюю матрицы и как правильно обрабатывать неоднозначности, возникающие в этом процессе. Во второй статье внешняя матрица рассматривалась более подробно, рассматривая несколько различных интерпретаций ее трехмерных вращений и перемещений.Сегодня мы так же рассмотрим внутреннюю матрицу, исследуя две эквивалентные интерпретации: как описание геометрии виртуальной камеры и как последовательность простых 2D-преобразований. После этого вы увидите интерактивную демонстрацию, иллюстрирующую обе интерпретации.
Если вам не интересно углубляться в теорию и вы просто хотите использовать свою внутреннюю матрицу с OpenGL, ознакомьтесь со статьями «Калиброванные камеры в OpenGL без glFrustum», «Калиброванные камеры» и «gluPerspective».
Все эти статьи являются частью серии «Камера перспективы, интерактивный тур». Чтобы прочитать другие статьи этой серии, перейдите к оглавлению.
Внутренняя матрица преобразует координаты трехмерной камеры в двумерные координаты однородного изображения. Эта перспективная проекция моделируется идеальной камерой-обскурой, показанной ниже.
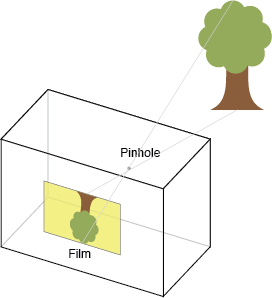
Внутренняя матрица параметризована Хартли и Зиссерманом как
\ [
K = \ left (
\ begin {array} {c c c}
f_x & s & x_0 \\
0 & f_y & y_0 \\
0 & 0 & 1 \\
\ {Конец массива}
\право )
\]
Каждый внутренний параметр описывает геометрическое свойство камеры.Давайте подробно рассмотрим каждое из этих свойств.
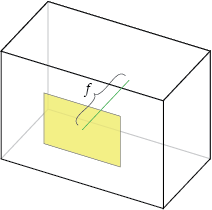
Фокусное расстояние, \ (f_x \), \ (f_y \)
Фокусное расстояние — это расстояние между отверстием и пленкой (или плоскостью изображения). По причинам, которые мы обсудим позже, фокусное расстояние измеряется в пикселях. В настоящей камере-обскуре и \ (f_x \), и \ (f_y \) имеют одинаковое значение, которое показано как \ (f \) ниже.
На практике \ (f_x \) и \ (f_y \) могут различаться по ряду причин:
- Дефекты сенсора цифровой камеры.
- Изображение было неравномерно масштабировано при постобработке.
- Объектив камеры создает непреднамеренное искажение.
- В камере используется анаморфный формат, при котором объектив сжимает широкоэкранную сцену в матрицу стандартного размера.
- Ошибки калибровки камеры.
Во всех этих случаях результирующее изображение имеет неквадратные пиксели.
Наличие двух разных фокусных расстояний не очень интуитивно понятно, поэтому в некоторых текстах (например, Форсайт и Понсе) используется одно фокусное расстояние и «соотношение сторон», которое описывает величину отклонения от идеально квадратного пикселя.Такая параметризация хорошо отделяет геометрию камеры (то есть фокусное расстояние) от искажения (соотношения сторон).
Смещение главной точки, \ (x_0 \), \ (y_0 \)
«Главная ось» камеры — это линия, перпендикулярная плоскости изображения, которая проходит через точечное отверстие. Его пересечение с плоскостью изображения называется «главной точкой», как показано ниже.
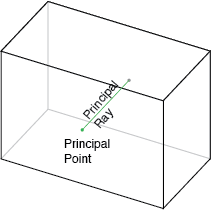
«Смещение главной точки» — это положение главной точки относительно исходной точки пленки.Точное определение зависит от того, какое соглашение используется для определения местоположения источника; на иллюстрации ниже предполагается, что он находится в нижнем левом углу фильма.
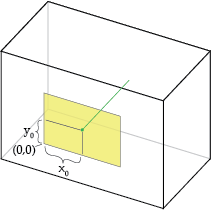
Увеличение \ (x_0 \) смещает точечное отверстие вправо:

Это эквивалентно смещению пленки влево и оставлению точечного отверстия без изменений.
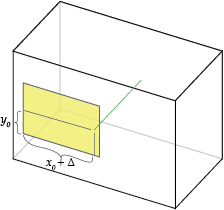
Обратите внимание, что рамка, окружающая камеру, не имеет значения, имеет значение только положение точечного отверстия относительно пленки.
Наклон оси, \ (s \)
Наклон оси вызывает сдвиговое искажение проецируемого изображения. Насколько мне известно, нет никакого аналога наклону оси для настоящей камеры-обскуры, но очевидно, что некоторые процессы оцифровки могут вызвать ненулевой перекос. Мы рассмотрим перекос подробнее позже.
Прочие геометрические свойства
Фокусное расстояние и смещение главной точки сводятся к простому перемещению пленки относительно точечного отверстия. Должны же быть другие способы трансформировать камеру, верно? А как насчет поворота или масштабирования пленки?
Вращение пленки вокруг точечного отверстия эквивалентно вращению самой камеры, которым управляет внешняя матрица.Вращение пленки вокруг любой другой фиксированной точки \ (x \) эквивалентно вращению вокруг отверстия \ (P \) с последующим перемещением на \ ((x-P) \).
А как насчет масштабирования? Должно быть очевидно, что удвоение всех размеров камеры (размера пленки и фокусного расстояния) не влияет на снимаемую сцену. Если вместо этого вы удвоите размер пленки и фокусное расстояние , а не , это будет эквивалентно удвоению обоих (без операции) и последующему уменьшению фокусного расстояния вдвое. Таким образом, явное представление масштаба фильма было бы излишним; он фиксируется фокусным расстоянием.
Фокусное расстояние — от пикселей до мировых единиц
Это обсуждение масштабирования камеры показывает, что существует бесконечное количество камер-обскур, которые производят одно и то же изображение. Внутренняя матрица касается только отношения между координатами камеры и координатами изображения, поэтому абсолютные размеры камеры не имеют значения. Использование пиксельных единиц для фокусного расстояния и смещения главной точки позволяет нам представить относительные размеры камеры, а именно положение пленки относительно ее размера в пикселях.
Другими словами, внутреннее преобразование камеры инвариантно к равномерному масштабированию геометрии камеры. Представляя размеры в пикселях, мы естественным образом фиксируем эту неизменность.
Вы можете использовать аналогичные треугольники для преобразования пиксельных единиц в мировые единицы (например, мм), если вы знаете хотя бы одно измерение камеры в мировых единицах. Например, если вы знаете, что пленка камеры (или цифровой датчик) имеет ширину \ (W \) в миллиметрах, а ширина изображения в пикселях равна \ (w \), вы можете преобразовать фокусное расстояние \ (f_x \) в мировые единицы используют:
\ [F_x = f_x \ frac {W} {w} \]
Другие параметры \ (f_y \), \ (x_0 \) и \ (y_0 \) могут быть преобразованы в их аналоги в мировых единицах \ (F_y \), \ (X_0 \) и \ (Y_0 \), используя аналогичные уравнения:
\ [
\ BEGIN {массив} {} ссс
F_y = f_y \ frac {H} {h} \ qquad
X_0 = x_0 \ frac {W} {w} \ qquad
Y_0 = y_0 \ frac {H} {h}
\ {Конец массива}
\]
Как мы обсуждали ранее, только расположение точечного отверстия и материи пленки, поэтому физическая коробка, окружающая камеру, не имеет значения.По этой причине во многих обсуждениях геометрии камеры используется более простое визуальное представление: пирамида камеры.
Область обзора камеры имеет форму пирамиды, которую иногда называют «конусом видимости». Давайте добавим к нашей сцене несколько трехмерных сфер и покажем, как они попадают в конус видимости, и создадим изображение.
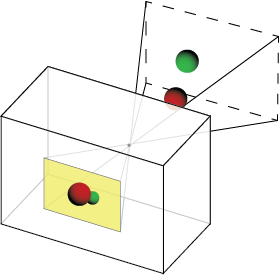
Так как «коробочка» камеры не имеет значения, снимаем ее. Также обратите внимание, что изображение в фильме представляет собой зеркальную версию реальности. Чтобы исправить это, мы будем использовать «виртуальный образ» вместо самого фильма.Виртуальное изображение имеет те же свойства, что и изображение на пленке, но в отличие от настоящего изображения виртуальное изображение появляется перед камерой, а проецируемое изображение переворачивается.
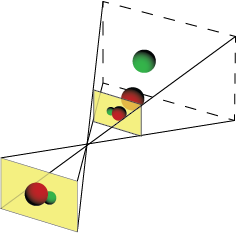
Обратите внимание, что положение и размер плоскости виртуального изображения произвольны — мы могли бы удвоить ее размер, если бы мы также удвоили расстояние от отверстия.
После удаления истинного изображения мы остаемся с представлением «усеченной пирамиды» нашей камеры-обскуры.
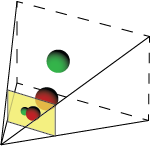
Точечное отверстие было заменено кончиком конуса видимости, и пленка теперь представлена виртуальной плоскостью изображения.Позже мы будем использовать это представление для нашей демонстрации.
В предыдущих разделах мы интерпретировали наши входящие 3-вектора как координаты трехмерного изображения, которые преобразуются в координаты однородного двухмерного изображения. В качестве альтернативы мы можем интерпретировать эти 3-вектора как однородные 2D-координаты, которые преобразуются в новый набор 2D-точек. Это дает нам новый взгляд на внутреннюю матрицу: последовательность двумерных аффинных преобразований.
Мы можем разложить внутреннюю матрицу на последовательность преобразований сдвига, масштабирования и смещения, соответствующих перекосу оси, фокусному расстоянию и смещению главной точки, соответственно:
\ [
\ Начать {} Align
K & = \ left (
\ begin {array} {c c c}
f_x & s & x_0 \\
0 & f_y & y_0 \\
0 & 0 & 1 \\
\ {Конец массива}
\право )
\\ [0.5em]
знак равно
\ Underbrace {
\осталось (
\ begin {array} {c c c}
1 & 0 & x_0 \\
0 & 1 & y_0 \\
0 и 0 и 1
\ {Конец массива}
\право )
} _ \ text {2D-перевод}
\ раз
\ Underbrace {
\осталось (
\ begin {array} {c c c}
f_x & 0 & 0 \\
0 & f_y & 0 \\
0 и 0 и 1
\ {Конец массива}
\право )
} _ \ text {2D-масштабирование}
\ раз
\ Underbrace {
\осталось (
\ begin {array} {c c c}
1 & s / f_x & 0 \\
0 & 1 & 0 \\
0 и 0 и 1
\ {Конец массива}
\право )
} _ \ text {2D сдвиг}
\ Конец {} Align
\]
Эквивалентное разложение помещает сдвиг после масштабирования :
\ [
\ Начать {} Align
K & =
\ Underbrace {
\осталось (
\ begin {array} {c c c}
1 & 0 & x_0 \\
0 & 1 & y_0 \\
0 и 0 и 1
\ {Конец массива}
\право )
} _ \ text {2D-перевод}
\ раз
\ Underbrace {
\осталось (
\ begin {array} {c c c}
1 & s / f_y & 0 \\
0 & 1 & 0 \\
0 и 0 и 1
\ {Конец массива}
\право )
} _ \ text {2D сдвиг}
\ раз
\ Underbrace {
\осталось (
\ begin {array} {c c c}
f_x & 0 & 0 \\
0 & f_y & 0 \\
0 и 0 и 1
\ {Конец массива}
\право )
} _ \ text {2D-масштабирование}
\ Конец {} Align
\]
Эта интерпретация прекрасно разделяет внешние и внутренние параметры на области 3D и 2D, соответственно.Также подчеркивается, что внутреннее преобразование камеры происходит пост-проекции . Одним из примечательных результатов этого является то, что внутренние параметры не могут влиять на видимость. — закрытые объекты не могут быть обнаружены простыми двухмерными преобразованиями в пространстве изображения.
Демо ниже иллюстрирует обе интерпретации внутренней матрицы. Слева — интерпретация «геометрии камеры». Обратите внимание, как точечное отверстие перемещается относительно плоскости изображения при настройке \ (x_0 \) и \ (y_0 \).
Справа — интерпретация «2D-преобразования». Обратите внимание, как изменение результатов фокусного расстояния приводит к масштабированию проецируемого изображения, а изменение главной точки приводит к чистому преобразованию.
Javascript требуется для этой демонстрации.
Слева : сцена с камерой и просматриваемым объемом. Виртуальная плоскость изображения отображается желтым цветом. Справа : изображение камеры.
В этой серии статей мы увидели, как разложить
- полная матрица камеры на внутреннюю и внешнюю матрицы,
- внешняя матрица в трехмерное вращение с последующим переносом, а
- внутреннюю матрицу на три основных 2D преобразования.\ text {Внешняя матрица} \\ [0.5em]
знак равно
\ Overbrace {\ Underbrace {
\осталось (
\ begin {array} {c c c}
1 & 0.
