Парадокс банаха тарского: Обратный парадокс Банаха-Тарского или как сократить хранимый объем данных в пять раз

Парадокс Банаха — Тарского — это… Что такое Парадокс Банаха — Тарского?

Шар можно «разбить» на куски и собрать из них два таких же шара.

Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям.

Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число «кусков» и составить из них второе. При этом для удвоения шара достаточно пяти кусков, но четырёх недостаточно.

Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств , так, что для каждого i подмножество A_i конгруэнтно B_i.

Верен также более сильный вариант парадокса:

Ввиду своей неправдоподобности, этот парадокс часто используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.

Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее. Поэтому более правильно называть парадоксом Хаусдорфа — Банаха — Тарского.

Значение для теории меры

Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара радиуса. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).

Для плоского круга аналогичная теорема неверна. Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь. Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.

Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число (хватает 10⁵⁰) частей и составить из них квадрат равной площади^[1][2], при этом возможно сдвигать части только с помощью параллельных переносов (см. Квадратура круга Тарского (англ.)).

Ссылки

1. ↑ Miklos Laczkovich: «Equidecomposability and discrepancy: a solution to Tarski’s circle squaring problem», Crelle’s Journal of Reine and Angewandte Mathematik 404 (1990) pp. 77-117.
2. ↑ Miklos Laczkovich: «Paradoxical decompositions: a survey of recent results.» First European Congress of Mathematics, Vol. II (Paris, 1992), pp. 159-184, Progr. Math., 120, Birkh.user, Basel, 1994.

Литература

Парадокс Банаха — Тарского — Википедия

Шар можно «разбить» на куски и собрать из них два таких же шара.

Парадо́кс Ба́наха — Та́рского (также называется парадо́ксом удвое́ния ша́ра и парадоксом Хаусдорфа — Ба́наха — Та́рского) — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.

Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число (не обязательно связных) попарно непересекающихся частей, передвинуть их (при этом частям не запрещается «проходить друг сквозь друга», то есть не требуется оставаться попарно непересекающимися во всех промежуточных положениях), и составить из них второе.

Более точно, два множества A{\displaystyle A} и B{\displaystyle B} являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств A=⋃inAi{\displaystyle A=\bigcup _{i}^{n}A_{i}}, B=⋃inBi{\displaystyle B=\bigcup _{i}^{n}B_{i}} так, что для каждого i{\displaystyle i} подмножество Ai{\displaystyle A_{i}} конгруэнтно Bi{\displaystyle B_{i}}.

Доказано, что для удвоения шара достаточно пяти частей, но четырёх недостаточно.

Верен также более сильный вариант парадокса:

Ввиду того, что вывод этой теоремы может показаться неправдоподобным, она иногда используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения.
Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.

Удвоение шара, хотя и кажется весьма подозрительным с точки зрения повседневной интуиции (в самом деле, нельзя же из одного апельсина сделать два при помощи одного только ножа), тем не менее не является парадоксом в логическом смысле этого слова, поскольку не приводит к логическому противоречию наподобие того, как к логическому противоречию приводит так называемый парадокс брадобрея или парадокс Рассела.

История

Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее.

Значение для теории меры

Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара.

Однако это справедливо только в случае, когда шар делится на части, имеющие объём.

Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают.

Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).

Для плоского круга аналогичное свойство неверно.

Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь.

Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.

Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число частей и составить из них квадрат равной площади^[1][2] (квадратура круга Тарского).

Примечания

1. ↑ Miklos Laczkovich: «Equidecomposability and discrepancy: a solution to Tarski’s circle squaring problem», Crelle’s Journal of Reine and Angewandte Mathematik 404 (1990) pp. 77-117.
2. ↑ Miklos Laczkovich: «Paradoxical decompositions: a survey of recent results.» First European Congress of Mathematics, Vol. II (Paris, 1992), pp. 159—184, Progr. Math., 120, Birkh.user, Basel, 1994.

Литература

Парадокс Банаха — Тарского | Математика, которая мне нравится

Знаете ли вы, что можно разрезать шар на пять частей, из которых складывают, не растягивая их, два шара того же радиуса, что и исходный?

Эта теорема известна как парадокс Банаха — Тарского.

Так почему же мы не можем сделать это в реальной жизни, скажем, с шаром из золота? Проблема в том, что сделать это можно только с материалом, который делúм до бесконечности, чего нет в действительности. Необходимые части настолько экзотические, что у них нет меры, или объема. Парадокс Банаха — Тарского говорит о том, что как бы мы ни определяли объем, всегда найдутся множества, которые не имеют объема (неизмеримые множества), или же приведенный выше пример покажет, что . 

Теорему Банаха — Тарского можно сформулировать иначе (сядьте, пожалуйста ). Возьмем шарик размером с горошину. Мы можем разрезать его на конечное число кусков так, что собрав эти куски, получим шар размером с Солнце.

Ясно, что такое трудно себе представить. В данном случае математика нам показывает, что нужно быть очень осторожными с определениями таких понятий, как объем, например, кажущихся нам интуитивно понятными.

Если мы не будем исключать растяжение, то все становится гораздо понятнее. Так, взяв интервал , мы растянем его в два раза, потом разрежем пополам и получим два интервала такой же длины, что и исходный. Если мы не будем ограничивать число кусков, на которые разрезаем шар, то все тоже выглядит гораздо понятнее, поскольку число точек в одном шаре такое же, как и количество точек в двух шарах.

Доказательство парадокса Банаха — Тарского основано на изучении действия группы преобразований на сфере, в частности, подгруппы группы вращений . Эти подгруппы (свободные подгруппы двух образующих) позволяют строить “парадоксальные’’ множества — множества, конгруэнтные двум или более копиям самих себя при групповых преобразованиях. Доказательство также опирается на аксиому выбора. Идея доказательства связана с равносоставленностью.

Источник: http://www.math.hmc.edu/funfacts/ffiles/30001.1-3-8.shtml

Парадокс Банаха — Тарского — Энциклопедия научных парадоксов

Материал из Энциклопедия научных парадоксов

Шар можно «разбить» на куски и собрать из них два таких же шара.

Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям.

Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число «кусков» и составить из них второе.
При этом для удвоения шара достаточно пяти кусков, но четырёх недостаточно.

Более точно, два множества A{\displaystyle A} и B{\displaystyle B} являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств A=⋃inAi{\displaystyle A=\bigcup _{i}^{n}A_{i}}, B=⋃inBi{\displaystyle B=\bigcup _{i}^{n}B_{i}} так, что для каждого i{\displaystyle i} подмножество Ai{\displaystyle A_{i}} конгруэнтно Bi{\displaystyle B_{i}}.

Верен также более сильный вариант парадокса:

Любые два ограниченных подмножества евклидова пространства с непустой внутренностью являются равносоставленными.

Ввиду своей неправдоподобности, этот парадокс часто используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.

Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее. Поэтому более правильно называть парадоксом Хаусдорфа — Банаха — Тарского.

Значение для теории меры[править]

Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара радиуса.
Однако это справедливо только в случае, когда шар делится на части, имеющие объём.
Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).

Для плоского круга аналогичная теорема неверна.
Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь. Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.

Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число (хватает 10⁵⁰) частей и составить из них квадрат равной площади^[1][2], при этом возможно сдвигать части только с помощью параллельных переносов.

1. ↑ Miklos Laczkovich: «Equidecomposability and discrepancy: a solution to Tarski’s circle squaring problem», Crelle’s Journal of Reine and Angewandte Mathematik 404 (1990) pp. 77-117.
2. ↑ Miklos Laczkovich: «Paradoxical decompositions: a survey of recent results.» First European Congress of Mathematics, Vol. II (Paris, 1992), pp. 159—184, Progr. Math., 120, Birkh.user, Basel, 1994.

Парадокс Банаха — Тарского — Википедия

Шар можно «разбить» на куски и собрать из них два таких же шара.

Парадо́кс Ба́наха — Та́рского (также называется парадо́ксом удвое́ния ша́ра и парадоксом Хаусдорфа — Ба́наха — Та́рского) — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.

Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число (не обязательно связных) попарно непересекающихся частей, передвинуть их (при этом частям не запрещается «проходить друг сквозь друга», то есть не требуется оставаться попарно непересекающимися во всех промежуточных положениях), и составить из них второе.

Более точно, два множества A{\displaystyle A} и B{\displaystyle B} являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств A=⋃inAi{\displaystyle A=\bigcup _{i}^{n}A_{i}}, B=⋃inBi{\displaystyle B=\bigcup _{i}^{n}B_{i}} так, что для каждого i{\displaystyle i} подмножество Ai{\displaystyle A_{i}} конгруэнтно Bi{\displaystyle B_{i}}.

Доказано, что для удвоения шара достаточно пяти частей, но четырёх недостаточно.

Верен также более сильный вариант парадокса:

Ввиду того, что вывод этой теоремы может показаться неправдоподобным, она иногда используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения.
Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.

Удвоение шара, хотя и кажется весьма подозрительным с точки зрения повседневной интуиции (в самом деле, нельзя же из одного апельсина сделать два при помощи одного только ножа), тем не менее не является парадоксом в логическом смысле этого слова, поскольку не приводит к логическому противоречию наподобие того, как к логическому противоречию приводит так называемый парадокс брадобрея или парадокс Рассела.

История

Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее.

Значение для теории меры

Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара.

Однако это справедливо только в случае, когда шар делится на части, имеющие объём.

Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают.

Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).

Для плоского круга аналогичное свойство неверно.

Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь.

Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.

Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число частей и составить из них квадрат равной площади^[1][2] (квадратура круга Тарского).

Примечания

1. ↑ Miklos Laczkovich: «Equidecomposability and discrepancy: a solution to Tarski’s circle squaring problem», Crelle’s Journal of Reine and Angewandte Mathematik 404 (1990) pp. 77-117.
2. ↑ Miklos Laczkovich: «Paradoxical decompositions: a survey of recent results.» First European Congress of Mathematics, Vol. II (Paris, 1992), pp. 159—184, Progr. Math., 120, Birkh.user, Basel, 1994.

Литература

Парадокс Банаха — Тарского — Википедия. Что такое Парадокс Банаха — Тарского

Шар можно «разбить» на куски и собрать из них два таких же шара.

Парадо́кс Ба́наха — Та́рского (также называется парадо́ксом удвое́ния ша́ра и парадоксом Хаусдорфа — Ба́наха — Та́рского) — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.

Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число (не обязательно связных) попарно непересекающихся частей, передвинуть их (при этом частям не запрещается «проходить друг сквозь друга», то есть не требуется оставаться попарно непересекающимися во всех промежуточных положениях), и составить из них второе.

Более точно, два множества A{\displaystyle A} и B{\displaystyle B} являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств A=⋃inAi{\displaystyle A=\bigcup _{i}^{n}A_{i}}, B=⋃inBi{\displaystyle B=\bigcup _{i}^{n}B_{i}} так, что для каждого i{\displaystyle i} подмножество Ai{\displaystyle A_{i}} конгруэнтно Bi{\displaystyle B_{i}}.

Доказано, что для удвоения шара достаточно пяти частей, но четырёх недостаточно.

Верен также более сильный вариант парадокса:

Ввиду того, что вывод этой теоремы может показаться неправдоподобным, она иногда используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения.
Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.

Удвоение шара, хотя и кажется весьма подозрительным с точки зрения повседневной интуиции (в самом деле, нельзя же из одного апельсина сделать два при помощи одного только ножа), тем не менее не является парадоксом в логическом смысле этого слова, поскольку не приводит к логическому противоречию наподобие того, как к логическому противоречию приводит так называемый парадокс брадобрея или парадокс Рассела.

История

Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее.

Значение для теории меры

Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара.

Однако это справедливо только в случае, когда шар делится на части, имеющие объём.

Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают.

Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).

Для плоского круга аналогичное свойство неверно.

Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь.

Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.

Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число частей и составить из них квадрат равной площади^[1][2] (квадратура круга Тарского).

Примечания

1. ↑ Miklos Laczkovich: «Equidecomposability and discrepancy: a solution to Tarski’s circle squaring problem», Crelle’s Journal of Reine and Angewandte Mathematik 404 (1990) pp. 77-117.
2. ↑ Miklos Laczkovich: «Paradoxical decompositions: a survey of recent results.» First European Congress of Mathematics, Vol. II (Paris, 1992), pp. 159—184, Progr. Math., 120, Birkh.user, Basel, 1994.

Литература

Парадокс Банаха—Тарского — это… Что такое Парадокс Банаха—Тарского?

Шар можно «разбить» на куски и собрать из них два таких же шара.

Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям.

Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число «кусков» и составить из них второе. При этом для удвоения шара достаточно пяти кусков, но четырёх недостаточно.

Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств 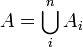, 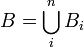так, что для каждого i подмножество A_i конгруэнтно B_i.

Верен также более сильный вариант парадокса:

Ввиду своей неправдоподобности, этот парадокс часто используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.

Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее. Поэтому более правильно называть парадоксом Хаусдорфа — Банаха — Тарского.

Значение для теории меры

Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара радиуса. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).

Для плоского круга аналогичная теорема неверна. Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь. Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.

Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число кусков и составить из них квадрат равной площади.

Литература

Wikimedia Foundation.
2010.

Страница не найдена | MIT

Перейти к содержанию ↓

• образование
• Исследовательская работа
• новаторство
• Прием + помощь
• Студенческая жизнь
• Новости
• Alumni
• О MIT
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Alumni
  • О MIT

Меню ↓

Поиск

Меню

Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!

Что вы ищете?

Увидеть больше результатов

Предложения или отзывы?

,

Paradoja de banach-tarski — Википедия, свободная энциклопедия

Википедия todavía no tiene una página llamada «Paradoja de banach-tarski».

Busca Paradoja de banach-tarski en otros proyectos hermanos de Wikipedia:

	Wikcionario (diccionario)
	Wikilibros (обучающие / руководства)
	Викицитатник (цитаты)
	Wikisource (biblioteca)
	Викинотики (noticias)
	Wikiversidad (Contenido académico)
	Commons (изображения и мультимедиа)
	Wikiviajes (viajes)
	Викиданные (данные)
	Викивиды (особые)

• Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla.
• Busca «Paradoja de banach-tarski» en el texto de otras páginas de Wikipedia que ya existen.
• Проконсультируйтесь по списку произведений искусства на «Paradoja de banach-tarski».
• Busca las páginas de Wikipedia que tienen объединяет «Paradoja de banach-tarski».
• Si ya habías creado la página con este nombre, limpia la caché de tu navegador.
• También puede que la página que buscas haya sido borrada.

Si el artículo incluso así no existe:

• Crea el artículo utilizando nuestro asistente o solicita su creación.
• Puedes traducir este artículo de otras Wikipedias.
• En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatible con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия.
• Ten en cuenta también que:
  • Artículos vacíos o con información minima serán borrados —véase «Википедия: Esbozo» -.
  • Artículos de publicidad y autopromoción serán borrados —véase «Википедия: Lo que Wikipedia no es» -.

,