Посетители «Википедии» как-то заметили, что если кликать по первой ссылке в каждой статье, то рано или поздно вы всё равно упрётесь в одну из статей, посвящённых философии. Объяснение этому феномену очень простое: практически все достижения современной культуры, науки и техники созданы на основе философских теорий и парадоксов, придуманных ещё в незапамятные времена.
В этой статье мы собрали для вас несколько любопытных примеров и историй, которые использовали философы для того, чтобы проиллюстрировать свои идеи. Многим из них уже более двух тысяч лет, но они всё равно не теряют своей актуальности.
Буриданов осёл
Буриданов осёл — философский парадокс, названный по имени Жана Буридана несмотря на то, что был известен ещё из трудов Аристотеля.
Осёл стоит между двух совершенно одинаковых стогов сена. Не в силах выбрать ни один из них, он теряет время, оценивая каждый из вариантов. В результате промедления осёл становится всё голоднее, а цена решения всё возрастает. Так и не сумев выбрать ни один из равнозначных вариантов, осёл в конце концов умирает от голода.
Этот пример доведён, разумеется, до абсурда, но он прекрасно иллюстрирует, что иногда свобода выбора оборачивается полным отсутствием какой-либо свободы. Если пытаться максимально рационально взвешивать похожие варианты, то можно лишиться обоих. В данном случае любой шаг лучше, чем бесконечный поиск оптимального решения.
Миф о пещере
Миф о пещере — знаменитая аллегория, использованная Платоном в диалоге «Государство» для пояснения своего учения об идеях. Считается краеугольным камнем платонизма и объективного идеализма в целом.
Представьте себе племя, которое приговорено жить в глубокой пещере. На ногах и руках у его членов оковы, которые мешают двигаться. В этой пещере родилось уже несколько поколений, единственным источником знаний для которых являются слабые отблески света и приглушённые звуки, достигающие их органов чувств с поверхности.
А теперь представьте, что эти люди знают о жизни снаружи?
И вот один из них снял с себя оковы и добрался до входа в пещеру. Он увидел солнце, деревья, удивительных животных, парящих в небе птиц. Затем он вернулся к своим соплеменникам и рассказал им об увиденном. Поверят ли они ему? Или сочтут более достоверной ту мрачную картину подземного мира, которую всю жизнь видят своими глазами?
Никогда не отбрасывайте идеи только из-за того, что они показались вам абсурдными и не вписываются в привычную картину мира. Может быть, весь ваш опыт — это только смутные отблески на стене пещеры.
Парадокс всемогущества
Этот парадокс заключается в попытке понять, может ли существо, которое в состоянии выполнить любое действие, сделать что-либо, что ограничило бы его способность выполнять действия.
Может ли всемогущее существо создать камень, который оно само не сможет поднять?
Возможно, вам покажется, что эта философская задачка является чисто умозрительным баловством, совершенно оторванным от жизни и практики. Однако это не так. Парадокс всемогущества имеет огромное значение для религии, политики и общественной жизни.
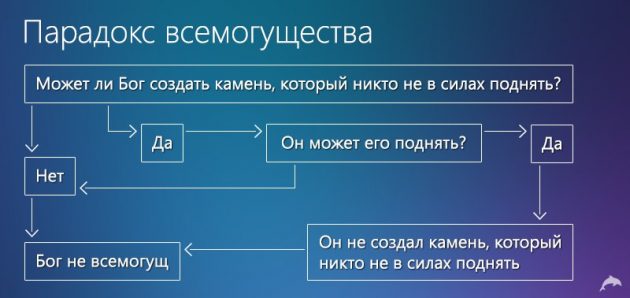
Пока этот парадокс остаётся неразрешённым. Нам остаётся только предположить, что абсолютного всемогущества не существует. А значит, у нас по-прежнему всегда есть шанс победить.
Парадокс курицы и яйца
Об этом парадоксе, вероятно, слышали все. Впервые обсуждение этой задачки появилось в трудах классических философов Древней Греции.
Что было раньше: курица или яйцо?
На первый взгляд, задача кажется неразрешимой, так как появление одного элемента невозможно без существования другого. Однако сложность этого парадокса заключается в расплывчатой формулировке. Решение задачи зависит от того, что вкладывается в понятие «куриное яйцо». Если куриное яйцо — это яйцо, снесённое курицей, то первой была, естественно, курица, вылупившаяся не из куриного яйца. Если куриное яйцо — яйцо, из которого вылупляется курица, то первым было куриное яйцо, снесённое не курицей.
Каждый раз, когда перед вами ставят неразрешимую задачу, внимательно вчитайтесь в её условие. Иногда именно здесь и находится путь к ответу.
Ахиллес и черепаха
Этот парадокс приписывают Зенону Элейскому — древнегреческому философу, знаменитому представителю Элейской школы. С его помощью он пытался доказать противоречивость концепций движения, пространства и множества.
Допустим, Ахиллес бежит в 10 раз быстрее, чем черепаха, и находится позади неё на расстоянии в 1 000 шагов. Пока Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт 100 шагов. Когда Ахиллес пробежит 100 шагов, черепаха проползёт ещё 10 шагов и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Несмотря на явную абсурдность данного утверждения, опровергнуть его не так просто. В поисках решения ведутся серьёзные дебаты, строятся различные физические и математические модели, пишутся статьи и защищаются диссертации.
Для нас же вывод из этой задачки очень прост. Даже если все научные светила упрямо утверждают, что вы никогда не догоните черепаху, не стоит опускать руки. Просто попробуйте сделать это.
Ты уже наверняка не один раз слышал о философских парадоксах. Например, про того же буриданова осла или Ахиллеса, который бегает наперегонки с черепахой. Решить их правильно и верно не представляется возможным — на то они и парадоксы, чтобы при каждом, даже на первый взгляд отличном, решении противоречить ответу. Чего только древние не придумали, да? Умные все-таки были люди. Но может быть, они, сочиняя эти апории, пытались вложить туда еще какой-нибудь смысл? Мы вот изучили несколько разных парадоксов, которые помогли еще раз убедиться в некоторых вещах, прийти к выводам, которые на условия и различные ответы не влияют, но зато помогают задать правильный вектор своей жизни. Этим мы с тобой и хотим поделиться.
1. Парадокс двух конвертов
Итак, дано условие. Перед тобой лежат два конверта. В одном из них находится определенная сумма денег, а в другом она в два раза больше. Естественно, сколько лежит в каком из конвертов, тебе неизвестно. Что нужно сделать тебе? Взять один из конвертов и проверить, что в нем находится. После этого у тебя есть выбор: оставить себе этот конверт или же взять и открыть другой. Какой из них принесет тебе сумму побольше, ты знать наверняка не можешь, так как одним из условий стоит неизвестность суммы в обоих конвертах. Парадокс заключается в том, что больше денег ты получишь только в том случае, если сделаешь бесконечное число выборов, переходя от одного конверта к другому. Но оставим эту задачу ученым. Какой вывод можем из нее сделать мы? Иногда нужно умерить свои аппетиты и довольствоваться малым. Правда, ты никогда не узнаешь, было ли в другом конверте больше денег либо же ты вытянул такой. Но согласись: порой лучше думать, что ты все сделал правильно, чем облажаться, чтобы убедиться в этом. А вообще, деньги — это не главное, ты это знаешь. Как и то, что с ними, конечно, жить проще.
2. Ахиллес и черепаха
Наверное, самая известная апория Зенона Элейского, с которого и пошли такие вот задачки. Суть этого парадокса такова: есть Ахиллес и черепаха, которые собираются бежать наперегонки. Человек дает животному фору в 500 метров. И, когда черепаха проползает данное расстояние, в соревнование подключается наш атлет, который бежит со скоростью в 10 раз большей, чем у пресмыкающегося. То есть, когда он пробегает 500 метров, черепаха успевает продвинуться еще на 50. Когда Ахиллес продвигается еще на 50 метров — черепаха проползает пять. И так до бесконечности, в которой показано, что человек никогда не догонит черепаху, как бы он ни старался. Да, это противоречит законам физики, но логически все выглядит верно. Зенон своей апорией хотел доказать, что некоторые из математических понятий, например «точка пространства» или «момент времени», не всегда подойдут к реальному движению. А мы хотим этим парадоксом еще раз напомнить тебе о том, что всегда найдутся люди, которые будут впереди тебя, как бы ты ни пытался их обогнать. С этим тебе придется смириться. Ты можешь ориентироваться на них, бежать за ними, тянуться к ним — все это похвально. Но признавать себя лучшим и гордиться собой так же, как Ахиллес, тебе не стоит.
5 парадоксов путешествия во времени, от которых закипят мозги
3. Вороны Гемпеля
А этот парадокс вывел философ Карл Густав Гемпель, однажды задавшись вопросом о противоречии человеческой логики и интуиции. Эту апорию Гемпель формирует так: тебе необходимо допустить, что все вороны только черного цвета. Исходя из обычной логики, мы должны сделать вывод, что все предметы, которые не имеют этот цвет, соответственно, воронами не являются. А когда на своем пути ты встретишь не одну такую черную птицу, то еще больше укоренишься в мнении о том, что все вороны черные. Встреча же с предметами другого цвета должна сильнее подпитать твою уверенность в том, что все, что не черного цвета, воронами не является. Это с точки зрения законов логики. Но если следовать интуиции, то эта встреча, по идее, не может заставить поверить человека в то, что абсолютно все вороны будут черного цвета.
Какое практическое значение этот парадокс имеет для нас? На примере с черными воронами, где этот взгляд по формальной логике принимается за истину, мы убеждаемся в силе догматизма. То есть человек всю жизнь думал, что вороны только черного цвета, так как об этом было сказано еще до него, а на своем опыте он убедился в этом. Но вот он встречает, например, этих же птиц, но с другим окрасом. Интуиция подсказывает ему, что это те же самые вороны, однако другого цвета. А вот логика говорит о том, что человек ошибается, приняв за воронов других пернатых. Вывод: слепая вера только лишь приближает тебя к серой массе — стремись проверять все, о чем тебе говорят, и смотри на мир шире.
4. Парадокс Бога
Об этой философской задаче тебе уж точно приходилось слышать. Наверное, даже не один раз. Суть ее проще, чем у предыдущих. Всемогущему существу предлагается создать такую каменную глыбу, которую никому нельзя будет сдвинуть с места. Но если это же существо не сможет ее переставить, тогда утверждение о его всемогущей природе сразу ставится под большой вопрос: как же ему подвластно все, если глыба остается на своем месте. Но даже если у него и получится ее передвинуть, то снова возникает вопрос, только уже с другой стороны. Где его всемогущество, если кусок камня все-таки сдвинули. Такой вот забавный парадокс. На него пытались ответить многие. Например, Декарт утверждал, что сущность этого существа, которое равно Богу, лежит вне человеческой логики.
Но нас интересует в этой апории немного другие аспекты — ближе к человеческому, чем к небесному. Предположим, такой камень существует. Значит ли это, что ты не попробуешь сдвинуть его с места, даже заранее зная, что это невозможно? Помни, что подобные вещи и утверждения не должны тебя останавливать. Почему? А ты вспомни сцену из фильма Милоша Формана «Пролетая над гнездом кукушки», в которой герой Джека Николсона пытается поднять неподъемный аппарат из ванной комнаты. Ведь он, как и ты, догадывается, что вряд ли у него из этого что-то выйдет. Но как говорит его герой: «Я хотя бы попытался». Не опускай руки раньше времени, а просто пытайся сделать хоть что-нибудь.
Как древние философы гнобили друг друга и людей
Краткий синопсис
По образованию я физик-теоретик, однако имею неплохую математическую базу. В магистратуре одним из предметов была философия, необходимо было выбрать тему и сдать по ней работу. Поскольку большинство вариантов не единожды было обмусолено, то решил выбрать что-то более экзотическое. На новизну не претендую, просто получилось аккумулировать всю/почти всю доступную литературу по этой теме. Философы и математики могут кидаться в меня камнями, буду лишь благодарен за конструктивную критику.
P.S. Весьма «сухой язык», но вполне читабельно после университетской программы. По большей части определения парадоксов брались из Википедии (упрощённая формулировка и готовая TeX-разметка).
Введение
Как сама теория множеств, так и парадоксы, ей присущие, появились не так уж и давно, чуть более ста лет назад. Однако за этот период был пройден большой путь, теория множеств так или иначе фактически стала основой большинства разделов математики. Парадоксы же её, связанные с бесконечностью Кантора, были успешно объяснены буквально за половину столетия.
Следует начать с определения.
Что есть множество? Вопрос достаточно простой, ответ на него вполне интуитивен. Множество это некий набор элементов, представляемый единым объектом. Кантор в своей работе Beiträge zur Begründung der transfiniten Mengenlehre даёт определение: под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M)[1]. Как видим, суть не изменилась, разница лишь в той части, которая зависит от мировоззрения определяющего. История же теории множеств как в логике так и в математике весьма противоречива. Фактически начало ей положил Кантор в XIX веке, далее Рассел и остальные продолжили работу.
Парадоксы (логики и теории множеств) — (греч. — неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.
Целью данной работы является изучение парадоксов теории множеств как наследников античных антиномий и вполне логичных следствий перехода к новому уровню абстракции — бесконечности. Задача — рассмотреть основные парадоксы, их философскую интерпретацию.
Основные парадоксы теории множеств
Брадобрей бреет только тех людей, которые не бреются сами. Бреет ли он себя?
Продолжим кратким экскурсом в историю.
Некторые из логических парадоксов были известны с античных времён, однако по причине того, что математическая теория ограничивалась одной лишь арифметикой и геометрией, соотнести их с теорией множеств было невозможно. В XIX веке ситуация изменилась коренным образом: Кантор в своих работах вышел на новый уровень абстракции. Он ввёл понятие бесконечности, создав тем самым новый раздел математики и позволив тем самым сравнивать различные бесконечности с помощью понятия «мощность множества» [2]. Однако тем самым он породил множество парадоксов. Самым первым является так называемый парадокс Бурали-Форти. В математической литературе встречаются различные формулировки, опирающиеся на разную терминологию и предполагаемый набор известных теорем. Вот одно из формальных определений.
Можно доказать, что если x — произвольное множество порядковых чисел, то множество-сумма есть порядковое число, большее или равное каждому из элементов x. Предположим теперь, что — множество всех порядковых чисел. Тогда — порядковое число, большее или равное любому из чисел в . Но тогда и — порядковое число, причём уже строго большее, а значит, и не равное любому из чисел в . Но это противоречит условию, по которому — множество всех порядковых чисел.
Сущность же парадокса в том, что при образовании множества всех порядковых чисел образуется новый порядковый тип, которого ещё не было среди «всех» трансфинитных порядковых чисел, существовавших до образования множества всех порядковых чисел. Этот парадокс был обнаружен самим Кантором, независимо открыт и опубликован итальянским математиком Бурали-Форти, ошибки же последнего были исправлены Расселом, после чего формулировка приобрела окончательный вид [2,3].
Среди всех попыток избежать подобных парадоксов и в какой-то мере попробовать их объяснить наибольшего внимания заслуживает идея уже упомянутого Рассела. Он предложил исключить из математики и логики импредикативные предложения, в которых определение элемента множества зависит от последнего, что и вызывает парадоксы. Правило звучит так: «никакое множество С не может содержать элементов m, определяемых лишь в терминах множества С, а так же элементов n, предполагающих в своём определении это множество» [4]. Подобное ограничение определения множества позволяет избежать парадоксов, но при этом значительно сужает область его применения в математике. Вдобавок этого недостаточно для объяснения их природы и причин появления, коренящихся в дихотомии мышления и языка, в особенностях формальной логики [4]. В какой-то мере в данном ограничении можно проследить аналогию с тем, что в более поздний период когнитивные психологи и лингвисты начали называть «категоризацией основного уровня»: определение сведено к наиболее легкой для понимания и изучения концепцией.
Далее Кантор в 1899 году открыл парадокс, названный его именем.
Предположим, что множество всех множеств существует. В этом случае справедливо , то есть всякое множество t является подмножеством V. Но из этого следует — мощность любого множества не превосходит мощности V. Но в силу аксиомы множества всех подмножеств, для V, как и любого множества, существует множество всех подмножеств , и по теореме Кантора , что противоречит предыдущему утверждению. Следовательно, V не может существовать, что вступает в противоречие с «наивной» гипотезой о том, что любое синтаксически корректное логическое условие определяет множество, то есть что для любой формулы A, не содержащей y свободно. Замечательное доказательство отсутствия подобных противоречий на основе аксиоматизированной теории множеств Цермело-Френкеля приводится у Поттера [3].
Оба вышеуказанных парадокса с логической точки зрения идентичны «Лжецу» либо «Брадобрею»: высказываемое суждение обращено не только на нечто объективное по отношению к нему, но и само на себя. Однако следует обращать внимание не только на логическую сторону, но и на понятие бесконечности, которое тут наличествует. В литературе ссылаются на работу Пуанкаре, в которой он пишет: «вера в существование актуальной бесконечности… делает необходимым эти непредикативные определения» [2].
В целом же имеют место основные моменты [2]:
- в данных парадоксах нарушается правило чётко разделять „сферы“ предиката и субъекта; степень смешения близка к подмене одного понятия другим;
- обычно в логике предполагается, что в процессе рассуждения субъект и предикат сохраняют свой объём и содержание, в данном же случае происходит
переход из одной категории в другую, что даёт в результате несоответствие; - наличие слова „все“ имеет смысл для конечного числа элементов, в случае же бесконечного их количества возможно наличие такого, которое
для определения себя потребует определение множества; - нарушаются основные логические законы:
- закон тождества нарушается тогда, когда обнаруживается нетождественность себе субъекта и предиката;
- закон противоречия — когда с одинаковым правом выводятся два противоречащих друг другу суждения;
- закон исключённого третьего — когда это третье приходится признавать, а не исключать, поскольку ни первое, ни второе не могут быть признаны одно без другого, т.к. они оказываются одинаково правомерными.
Третий парадокс носит имя Рассела. Один из вариантов определения приведён далее.
Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента.Содержит ли K само себя в качестве элемента? Если да, то, по определению K, оно не должно быть элементом K — противоречие.Если нет — то, по определению K, оно должно быть элементом K — вновь противоречие. Данное утверждение логически выводится из парадокса Кантора, что показывает их взаимосвязь. Однако философская сущность проявляется более чётко, поскольку „самодвижение» понятий происходит прямо “на наших глазах» [2].
Парадокс Тристрама Шенди:
В романе Стерна «Жизнь и мнения Тристрама Шенди, джентльмена» герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. В связи с этим герой сетует, что материал его биографии будет накапливаться быстрее, чем он сможет его обработать, и он никогда не сможет ее завершить. «Теперь я утверждаю, — возражает на это Рассел, — что если бы он жил вечно и его работа не стала бы ему в тягость, даже если бы его жизнь продолжала быть столь же богатой событиями, как вначале, то ни одна из частей его биографии не осталась бы ненаписанной».
Действительно, события n-го дня Шенди мог бы описать за n-й год и, таким образом, в его автобиографии каждый день оказался бы запечатленным.
Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней.
Рассел проводит аналогию между этим романом и Зеноном с его черепахой. По его мнению решение лежит в том, что целое эквивалентно его части в бесконечности. Т.е. к противоречию приводит только «аксиома здравого смысла» [2]. Однако же разрешение проблемы лежит в области чистой математики. Очевидно, что имеется два множества — года и дни, между элементами которых установлено взаимно-однозначное соответствие — биекция. Тогда при условии бесконечной жизни главного героя имеется два бесконечных равномощных множества, что, если рассматривать мощность как обобщение понятия количества элементов в множестве, разрешает парадокс.
Парадокс (теорема) Банаха-Тарского или парадокс удвоения шара — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.
Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число частей, передвинуть их, и составить из них второе.
Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств так, что для каждого i подмножество конгруэнтно .
Если же пользоваться теоремой выбора, то определение звучит так[3]:
Аксиома выбора подразумевает, что существует разбиение поверхности единичной сферы на конечное количество частей, которые преобразованиями трёхмерного Евклидова пространства, не меняющими форму этих составляющих, могут быть собраны в две сферы единичного радиуса.
Очевидно, что при требовании для данных частей быть измеримыми, данное постоение неосуществимо. Известный физик Ричард Фейнман в своей биографии рассказывал, как в своё время у него получилось победить в споре о разбиении апельсина на конечное количество частей и пересоставлении его [5].
В определённых моментах этот парадокс используется для опровержения аксиомы выбора, однако проблема в том, что то, что мы считаем элементарной геометрией, — несущественно. Те понятия, которые мы считаем интуитивными, должны быть расширены до уровня свойств трансцендентных функций [3].
Чтобы и дальше ослабить уверенность тех, кто считает аксиому выбора неверной, следует упомянуть теорему Мазуркевича и Серпинского, которая утверждает, что существует непустое подмножество Е Евклидовой плоскости, которое имеет два непересекающихся подмножества, каждое из которых может быть разбито на конечное количество частей, так что их можно перевести изометриями в покрытие множества Е.
При этом доказательство не требует использования аксиомы выбора[3].
Дальнейшие же построения на основе аксиомы определённости дают разрешение парадокса Банаха-Тарского, но не представляют такого интереса [3].
- Парадокс Ришара: требуется назвать «наименьшее число, не названное в этой книге». Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2].
- Парадокс Греллинга-Нильсона: слова либо знаки могут обозначать какое-либо свойство и при этом иметь его или нет. Самая тривиальная формулировка звучит так: является ли слово «гетерологичный» (что означает «неприменимый к самому себе»), гетерологичным?.. Весьма схож с парадоксом Рассела в связи с наличием диалектического противоречия: нарушается двойственность формы и содержания. В случае со словами, имеющими высокий уровень абстракции, невозможно решить, являются ли эти слова гетерологичными [2].
- Парадокс Сколема: используя теорему Гёделя о полноте и теорему Лёвенхейма-Сколема[3] получаем, что аксиоматическая теория множеств остаётся истинной и тогда, когда будет предполагаться (иметься) для её интерпретации только счётная совокупность множеств. В то же время
аксиоматическая теория включает в себя уже упомянутую теорему Кантора, что приводит нас к несчётным бесконечным множествам. [2]
Разрешение парадоксов
Создание теории множеств породило то, что считают третьим кризисом математики, который до сих пор не был разрешён удовлетворительно для всех [4].
Исторически сложилось, что первым подходом был теоретико-множественный. Он основывался на использовании актуальной бесконечности, когда считалось, что любая бесконечная последовательность является завершённой в бесконечности. Идея заключалась в том, что в теории множеств часто приходилось оперировать множествами, которые могли являться части других, более обширных множеств. Успешные действия в таком случае были возможны лишь в одном случае: данные множества (конечные и бесконечные) завершены. Определённый успех был очевиден: аксиоматическая теория множеств Цермело-Френкеля, целая школа математики Николя Бурбаки, которая существует уже больше половины столетия и до сих пор вызывает множество критики.
Логицизм был попыткой свести всю известную математику к терминам арифметики, а потом термины арифметики свести к понятиям математической логики. Вплотную этим занялся Фреге, однако после окончания работы над трудом, он вынужден был указать о своей несостоятельности, после того, как Рассел указал на имеющиеся в теории противоречия. Тот же Рассел, как уже был упомянуто ранее, попытался исключить использование импредикативных определений с помощью «теории типов». Однако его понятия множества и бесконечности, а так же аксиома сводимости оказались нелогичными. Основной проблемой было то, что не учитывались качественные различия между формальной и математической логикой, а так же наличие лишних понятий, в том числе и интуитивного характера.
В итоге теория логицизма не смогла устранить диалектических противоречий парадоксов, связанных с бесконечностью. Имели место лишь принципы и методы, которые позволяли избавиться хотя бы от непредикативных определений. В свох же рассуждениях Рассел был наследником Кантора [2]
В конце XIX — начале XX в. распространение формалистической точки зрения на математику было связано с развитием аксиоматического метода и той программой обоснования математики, которую выдвинул Д. Гильберт. На степень важности этого факта указывает то, что первой проблемой из двадцати трёх, которые он поставил перед математическим сообществом, была проблема бесконечности. Формализация была необходима для доказательства непротиворечивости классической математики, «исключив при этом из неё всю метафизику». Учитывая средства и методы, которыми пользовался Гильберт, его цель оказалась принципиально невыполнимой, но его программа имела огромное влияние на все последующее развитие оснований математики. Гильберт достаточно долго работал над этой проблемой, построив первоначально аксиоматику геометрии. Поскольку решение проблемы оказалось достаточно успешным, он решил применить аксиоматический метод к теории натуральных чисел. Вот что он писал в связи с этим: «Я преследую важную цель: именно я хотел бы разделаться с вопросами обоснования математики как таковыми, превратив каждое математическое высказывание в строго выводимую формулу.» От бесконечности при этом планировалось избавиться с помощью сведения её к некому конечному числу операций. Для этого он обращался к физике с её атомизмом, дабы показать всю несостоятельность бесконечных величин. Фактически Гильберт поставил вопрос о соотношении теории и объективной реальности.
Более или менее полное представление о финитных методах дает ученик Гильберта Ж. Эрбран. Под финитными рассуждениями он понимает такие рассуждения, которые удовлетворяют следующим условиям: логические парадоксы » — всегда рассматривается лишь конечное и определенное число предметов и функций;
— функции имеют точное определение, и это определение позволяет нам вычислить их значение;
— никогда не утверждается «Этот объект существует», если не известен способ его построения;
— никогда не рассматривается множество всех предметов X какой-либо бесконечной совокупности;
— если известно, что какое-либо рассуждение или теорема верны для всех этих X, то это означает, что это общее рассуждение можно повторить для каждого конкретного X, причем само это общее рассуждение следует рассматривать только как образец для проведения таких конкретных рассуждений.»
Однако в момент последней публикации в этой области Гёдель уже получил свои результаты, в сущности опять обнаружил и утвердил наличие диалектики в процессе познания. По сути своей дальнейшее развитие математики продемонстрировало несостоятельность программы Гильберта.
Что же, собственно, доказал Гёдель? Можно выделить три основных результата:
1. Гёдель показал невозможность математического доказательства непротиворечивости любой системы, достаточно обширной, чтобы включать в себя всю арифметику, доказательства, которое не использовало бы каких-либо иных правил вывода, кроме тех, что имеются в самой данной системе. Такое доказательство, которое использует более мощное правило вывода, может оказаться полезным. Но если эти правила вывода сильнее логических средств арифметического исчисления, то уверенности в непротиворечивости используемых в доказательстве допущений не будет. Во всяком случае, если используемые методы не будут финитистскими, то программа Гильберта окажется невыполнимой. Гёдель как раз и показывает несостоятельность расчетов на нахождение финитистского доказательства непротиворечивости арифметики.
2. Гёдель указал на принципиальную ограниченность возможностей аксиоматического метода: система Principia Mathematica, как и всякая иная система, с помощью которой строится арифметика, существенно неполна, т. е. для любой непротиворечивой системы арифметических аксиом имеются истинные арифметические предложения, которые не выводятся из аксиом этой системы.
3. Теорема Гёделя показывает, что никакое расширение арифметической системы не может сделать ее полной, и даже если мы наполним ее бесконечным множеством аксиом, то в новой системе всегда найдутся истинные, но не выводимые средствами этой системы положения. Аксиоматический подход к арифметике натуральных чисел не в состоянии охватить всю область истинных арифметических суждений, и то, что мы понимаем под процессом математического доказательства, не сводится к использованию аксиоматического метода. После теоремы Гёделя стало бессмысленно рассчитывать, что понятию убедительного математического доказательства можно будет придать раз и навсегда очерченные формы. [2,4,6]
Последним в этой череде попыток объяснить теорию множеств был интуиционизм.
Он прошел ряд этапов в своей эволюции — полуинтуиционизм, собственно интуиционизм, ультраинтуиционизм. На разных этапах математиков волновали разные проблемы, но одной из основных проблем математики является проблема бесконечности. Математические понятия бесконечности, непрерывности служили предметом философского анализа с момента их появления (идеи атомистов, апории Зенона Элейского, инфинитезимальные методы в античности, исчисление бесконечно малых в Новое время и пр.). Наибольшие споры вызывало применение различных видов бесконечности (потенциальной, актуальной) как математических объектов и их интерпретация. Все эти проблемы, на наш взгляд, были порождены более глубокой проблемой — о роли субъекта в научном познании. Дело в том, что состояние кризиса в математике порождено эпистемологической неопределенностью соизмерения мира объекта (бесконечности) и мира субъекта. Математик как субъект имеет возможность выбора средств познания — или потенциальной, или актуальной бесконечности. Применение потенциальной бесконечности как становящейся, дает ему возможность осуществлять, конструировать бесконечное множество построений, которые можно надстраивать над конечными, не имея конечного шага, не завершая построение, оно только возможно. Применение актуальной бесконечности дает ему возможность работать с бесконечностью как с уже осуществимой, завершенной в своем построении, как актуально данной одновременно.
На этапе полуинтуиционизма проблема бесконечности еще не была самостоятельной, а была вплетена в проблему построения математических объектов и способов его обоснования. Полуинтуиционизм А. Пуанкаре и представителей парижской школы теории функций Бэра, Лебега и Бореля был направлен против принятия аксиомы свободного выбора, с помощью которой доказывается теорема Цермело, утверждавшая, что всякое множество можно сделать вполне упорядоченным, но без указания теоретического способа определения элементов любого подмножества искомого множества. Нет способа построения математического объекта, нет и самого математического объекта. Математики считали, что наличие или отсутствие теоретического способа построения последовательности объектов исследования может служить основой обоснования или опровержения этой аксиомы. В российском варианте полуинтуиционистская концепция в философских основаниях математики получила развитие в таком направлении, как эффективизм, развиваемый Н.Н. Лузиным. Эффективизм представляет собой оппозицию к основным абстракциям учения множества Кантора о бесконечном — актуальности, выбора, трансфинитной индукции и др.
Для эффективизма гносеологически более ценными абстракциями является абстракция потенциальной осуществимости, чем абстракция актуальной бесконечности. Благодаря этому становится возможным введение понятия о трансфинитных ординалах (бесконечных порядковых числах) на основе эффективного понятия о росте функций. Гносеологическая установка эффективизма для отображения непрерывного (континуума) опиралась на дискретные средства (арифметики) и созданную Н.Н.Лузиным дескриптивную теорию множеств (функций). Интуиционизм голландца Л. Э. Я. Брауэра, Г. Вейля, А. Гейтинга в качестве традиционного объекта исследования видит свободно становящиеся последовательности различных видов. На этом этапе, решая собственно математические проблемы, в том числе о перестройке всей математики на новой основе, интуиционисты подняли философский вопрос о роли математика как познающего субъекта. Каково его положение, где он более свободен и активен в выборе средств познания? Интуиционисты первыми (и на этапе полуинтуиционизма) стали критиковать концепцию актуальной бесконечности, канторовскую теорию множеств, усмотрев в ней ущемление возможностей субъекта влиять на процесс научного поиска решения конструктивной задачи. В случае использования потенциальной бесконечности субъект себя не обманывает, так как для него идея потенциальной бесконечности интуитивно значительно яснее, чем идея актуальной бесконечности. Для интуициониста объект считается существующим, если он дан непосредственно математику или известен метод его построения, конструирования. Субъект в любом случае может приступить к процессу достраивания ряда элементов своего множества. Непостроенный объект для интуиционистов не существует. В то же время субъект, работающий с актуальной бесконечностью, будет лишен этой возможности и будет чувствовать двойную уязвимость принятой позиции:
1) никогда нельзя осуществить это бесконечное построение;
2) он принимает решение оперировать с актуальной бесконечностью как с конечным объектом и в этом случае теряет свою специфику понятия бесконечности. Интуиционизм сознательно ограничивает возможности математика тем, что тот может осуществлять построение математических объектов исключительно посредством таких средств, которые хотя и получаемы с помощью абстрактных понятий, но эффективны, убедительны, доказуемы, функционально конструктивны именно практически и сами интуитивно ясны как конструкции, построения, надежность которых на практике не вызывает никаких сомнений. Интуиционизм, опираясь на понятие потенциальной бесконечности и конструктивные методы исследования, имеет дело с математикой становления, теория множеств относится к математике бытия.
Для интуициониста Брауэра как представителя математического эмпиризма логика вторична, он критикует ее и закон исключённого третьего.
В своих отчасти мистических работах он не отрицает наличие бесконечности, однако не допускает её актуализации, лишь потенциализацию. Главное для него — интерпретация и обоснование практически используемых логических средств и математических рассуждений. Принятое интуиционистами ограничение преодолевает неопределенность использования понятия бесконечности в математике и выражает стремление преодолеть кризис в основании математики.
Ультраинтуиционизм (А.Н. Колмогоров, А.А.Марков и др.) — последняя стадия развития интуиционизма, на которой модернизируются, существенно дополняются и преобразуются основные его идеи, не изменяя его сущности, но преодолевая недостатки и усиливая позитивные стороны, руководствуясь критериями математической строгости. Слабостью подхода интуиционистов было узкое понимание роли интуиции как единственного источника обоснования правильности и эффективности математических методов. Принимая «интуитивную ясность» в качестве критерия истинности в математике, интуиционисты методологически обедняли возможности математика как субъекта познания, сводили его деятельность лишь к мыслительным операциям на основе интуиции и не включали практику в процесс математического познания. Ультраинтуиционистская программа обоснования математики является российским приоритетом. Поэтому отечественные математики, преодолевая ограниченность интуиционизма, принимали действенной методологию материалистической диалектики, признающей человеческую практику источником формирования как математических понятий, так и математических методов (умозаключений, построений). Проблему существования математических объектов ультраинтуиционисты решали, опираясь уже не на неопределяемое субъективное понятие интуиции, а на математическую практику и конкретный механизм построения математического объекта — алгоритм, выражаемый вычислимой, рекурсивной функцией.
Ультраинтуиционизм усиливает достоинства интуиционизма, заключающиеся в возможности упорядочивания и обобщения приемов решения конструктивных проблем, употребляемых математиками любого направления. Поэтому интуиционизм последней стадии (ультраинтуиционизм) близок конструктивизму в математике. В гносеологическом аспекте основные идеи и принципы ультраинтуиционизма таковы: критика классической аксиоматики логики; использование и значительное усиление (по явному указанию А.А. Маркова) роли абстракции отождествления (мысленного отвлечения от несходных свойств предметов и одновременного вычленения общих свойств предметов) как способа построения и конструктивного понимания абстрактных понятий, математических суждений; доказательство непротиворечивости непротиворечивых теорий. В формальном аспекте применение абстракции отождествления оправдывается тремя ее свойствами (аксиомами) равенства — рефлексивности, транзитивности и симметрии.
Для решения основного противоречия в математике по проблеме бесконечности, породившего кризис ее оснований, на этапе ультраинтуиционизма в работах А.Н. Колмогорова были предложены пути выхода из кризиса посредством решения проблемы отношений между классической и интуиционистской логикой, классической и интуиционистской математикой. Интуиционизм Брауэра в целом отрицал логику, но так как любой математик не может обойтись без логики, в интуиционизме все-таки сохранилась практика логических рассуждений, допускались некоторые принципы классической логики, имеющей в качестве своей базы аксиоматику. С.К. Клини, Р. Весли даже отмечают, что интуиционистскую математику можно описать в виде некоторого исчисления, а исчисление является способом организации математического знания на основах логики, формализации и ее формы — алгоритмизации. Новый вариант соотношения логики и математики в рамках интуиционистских требований к интуитивной ясности суждений, особенно тех, которые включали отрицание, А.Н. Колмогоров предложил следующим образом: интуиционистскую логику, тесно связанную с интуиционистской математикой, он представил в форме аксиоматического импликативного минимального исчисления высказываний и предикатов. Тем самым ученый представил новую модель математического знания, преодолевающую ограниченность интуиционизма в признании лишь интуиции как средства познания и ограниченность логицизма, абсолютизирующего возможности логики в математике. Эта позиция позволила в математической форме продемонстрировать синтез интуитивного и логического как основы гибкой рациональности и ее конструктивной эффективности.
Выводы. Таким образом, эпистемологический аспект математического познания позволяет оценить революционные изменения на этапе кризиса оснований математики на рубеже XIX-XX вв. с новых позиций в понимании процесса познания, природы и роли субъекта в нем. Гносеологический субъект традиционной теории познания, соответствующий периоду господства теоретико-множественного подхода в математике, — это абстрактный, неполный, «частичный» субъект, представленный в субъектно-объектных отношениях, оторванный абстракциями, логикой, формализмом от действительности, рационально, теоретически познающий свой объект и понимаемый как зеркало, точно отражающее и копирующее действительность. По сути, субъект исключался из познания как реального процесса и результата взаимодействия с объектом. Выход интуиционизма на арену борьбы философских направлений в математике привел к новому пониманию математика как субъекта познания — человека познающего, философская абстракция которого должна быть выстроена как бы заново. Математик предстал как эмпирический субъект, понимаемый уже как целостный реальный человек, включающий все те свойства, от которых отвлекались в гносеологическом субъекте, — эмпирическую конкретность, изменчивость, историчность; это действующий и познающий в реальном познании, творческий, интуитивный, изобретательный субъект. Философия интуиционистской математики стала базой, фундаментом современной эпистемологической парадигмы, построенной на концепции гибкой рациональности, в которой человек — это цельный (целостный) субъект познания, обладающий новыми познавательными качествами, методами, процедурами; он синтезирует свою как абстрактно-гносеологическую и логико-методологическую природу и форму, так и одновременно получает экзистенциально-антропологическое и «историко-метафизическое» осмысление.
Важным моментом так же является интуиция в познании и, в частности, в образовании математических понятий. Опять же идёт борьба с философией, попытки исключить закон исключённого третьего, как не имеющий смысла в математике и пришедший в неё из философии. Однако же наличие излишнего акцента на интуицию и отстутствие чётких математических обоснований не позволили перевести математику на твёрдый фундамент. [2,4,7]
Однако после появления в 1930-х годах строгого понятия алгоритма эстафету от интуиционизма принял математический конструктивизм, представители которого внесли немалый вклад в современную теорию вычислимости. Кроме того, в 1970-е и 1980-е годы обнаружились существенные связи между некоторыми идеями интуиционистов (даже теми, которые раньше казались абсурдными) и математической теорией топосов. Математика, имеющаяся в некоторых топосах, весьма напоминает ту, которую пытались создать интуиционисты.
В качестве итога можно сделать утверждение: большинство из вышеуказанных парадоксов попросту не существуют в теории множеств с самопринадлежностью [8]. Является ли подобный подход окончательным — спорный вопрос, дальнейшие работы в этой области покажут.
Заключение
Диалектико-материалистический анализ показывает, что парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т. п. Поэтому не может быть дано универсального способа устранения всех парадоксов.
Закончен ли третий кризис математики (потому как он находился в причинно-следственной связи с парадоксами; теперь же парадоксы — неотъемлемая часть) — тут мнения расходятся, хотя формально известные парадоксы к 1907-му году были устранены. Впрочем, сейчас в математике имеются и другие обстоятельства, которые можно считать либо кризисными, либо предвещающими кризис (например), отсутствие строгого обснования у континуального интеграла).
Что же касается парадоксов, то весьма важную роль в математике сыграл известный парадокс лжеца, а так же целая серия парадоксов в так называемой наивной (предшествовавшей аксиоматической) теории множеств, вызвавших кризис оснований (один из таких парадоксов сыграл роковую роль в жизни Г. Фреге). Но, возможно, одним из самых недооценённых явлений в современной математике, которое вполне можно назвать и парадоксальным, и кризисным, является решение Полом Коэном в 1963 году первой проблемы Гильберта. Точнее, не сам факт решения, а характер этого решения [9].
Литература
- Georg Cantor. Beiträge zur begründung der transfiniten mengenlehre. Mathematische Annalen, 46:481—512, 1895.
- И.Н. Бурова. Парадоксы теории множеств и диалектика. Наука, 1976.
- M.D. Potter. Set theory and its philosophy: a critical introduction. Oxford University Press, Incorporated, 2004.
- Жуков Н.И. Философские основания математики. Мн.: Университетское, 1990.
- Фейнман Р.Ф., С. Ильин. Вы, конечно, шутите, мистер Фейнман!: похождения удивительного человека, поведанные им Р. Лейтону. КоЛибри, 2008.
- О. М. Мижевич. Два способа преодоления парадоксов в теории множеств Г. Кантора. Логико-философские штудии, (3):279—299, 2005.
- С. И. Масалова. ФИЛОСОФИЯ ИНТУИЦИОНИСТСКОЙ МАТЕМАТИКИ. Вестник ДГТУ, (4), 2006.
- Чечулин В.Л. Теория множеств с самопринадлежностью (основания и некоторые приложения). Перм. гос. ун-т. – Пермь, 2012.
- С. Н. Тронин. Краткий конспект лекций по дисциплине »Философия математики». Казань, 2012.
- Гришин В.Н., Бочвар Д.А. Исследования по теории множеств и неклассическим логикам. Наука, 1976.
- Хофштадтер Д. Гедель, Эшер, Бах: эта бесконечная гирлянда. Бахрах-М, 2001.
- Кабаков Ф.А., Мендельсон Э. Введение в математическую логику. Издательство «Наука», 1976.
- Д.А. Бочвар. К вопросу о парадоксах математической логики и теории множеств. Математический сборник, 57(3):369—384, 1944.
10 занимательных логических парадоксов
Учёные и мыслители с давних времён любят развлекать себя и коллег постановкой неразрешимых задач и формулированием разного рода парадоксов. Некоторые из подобных мысленных экспериментов сохраняют актуальность на протяжении тысяч лет, что свидетельствует о несовершенстве многих популярных научных моделей и «дырах» в общепринятых теориях, давно считающихся фундаментальными. Предлагаем вам поразмыслить над наиболее интересными и удивительными парадоксами, которые, как сейчас выражаются, «взорвали мозг» не одному поколению логиков, философов и математиков.
1. Апория «Ахиллес и черепаха»
Парадокс Ахиллеса и черепахи — одна из апорий (логически верных, но противоречивых высказываний), сформулированных древнегреческим философом Зеноном Элейским в V-м веке до нашей эры. Суть её в следующем: легендарный герой Ахиллес решил посоревноваться в беге с черепахой. Как известно, черепахи не отличаются прыткостью, поэтому Ахиллес дал сопернику фору в 500 м. Когда черепаха преодолевает эту дистанцию, герой пускается в погоню со скоростью в 10 раз большей, то есть пока черепаха ползёт 50 м, Ахиллес успевает пробежать данные ей 500 м форы. Затем бегун преодолевает следующие 50 м, но черепаха в это время отползает ещё на 5 м, кажется, что Ахиллес вот-вот её догонит, однако соперница всё ещё впереди и пока он бежит 5 м, ей удаётся продвинуться ещё на полметра и так далее. Дистанция между ними бесконечно сокращается, но по идее, герою так и не удаётся догнать медлительную черепаху, она ненамного, но всегда опережает его.
© www.student31.ru
Конечно, с точки зрения физики парадокс не имеет смысла — если Ахиллес движется намного быстрее, он в любом случае вырвется вперёд, однако Зенон, в первую очередь, хотел продемонстрировать своими рассуждениями, что идеализированные математические понятия «точка пространства» и «момент времени» не слишком подходят для корректного применения к реальному движению. Апория выявляет расхождение между математически обоснованной идеей, что ненулевые интервалы пространства и времени можно делить бесконечно (поэтому черепаха должна всегда оставаться впереди) и реальностью, в которой герой, конечно, выигрывает гонку.
2. Парадокс временной петли
«Новые путешественники во времени» Дэвида Туми
Парадоксы, описывающие путешествия во времени, давно служат источником вдохновения для писателей-фантастов и создателей научно-фантастических фильмов и сериалов. Существует несколько вариантов парадоксов временной петли, один из самых простых и наглядных примеров подобной проблемы привёл в своей книге «The New Time Travelers» («Новые путешественники во времени») Дэвид Туми, профессор из Университета Массачусетса.
Представьте себе, что путешественник во времени купил в книжном магазине экземпляр шекспировского «Гамлета». Затем он отправился в Англию времён Королевы-девы Елизаветы I и отыскав Уильяма Шекспира, вручил ему книгу. Тот переписал её и издал, как собственное сочинение. Проходят сотни лет, «Гамлета» переводят на десятки языков, бесконечно переиздают, и одна из копий оказывается в том самом книжном магазине, где путешественник во времени покупает её и отдаёт Шекспиру, а тот снимает копию и так далее… Кого в таком случае нужно считать автором бессмертной трагедии?
3. Парадокс девочки и мальчика
Мартин Гарднер / © www.post-gazette.com
В теории вероятностей этот парадокс также называют «Дети мистера Смита» или «Проблемы миссис Смит». Впервые он был сформулирован американским математиком Мартином Гарднером в одном из номеров журнала «Scientific American». Учёные спорят над парадоксом уже несколько десятилетий и существует несколько способов его разрешения. Поразмыслив над проблемой, вы можете предложить и свой собственный вариант.
В семье есть двое детей и точно известно, что один из них — мальчик. Какова вероятность того, что второй ребёнок тоже имеет мужской пол? На первый взгляд, ответ вполне очевиден — 50 на 50, либо он действительно мальчик, либо девочка, шансы должны быть равными. Проблема в том, что для двухдетных семей существует четыре возможных комбинации полов детей — две девочки, два мальчика, старший мальчик и младшая девочка и наоборот — девочка старшего возраста и мальчик младшего. Первую можно исключить, так как один из детей совершенно точно мальчик, но в таком случае остаются три возможных варианта, а не два и вероятность того, что второе чадо тоже мальчик — один шанс из трёх.
4. Парадокс Журдена с карточкой
Проблему, предложенную британским логиком и математиком Филиппом Журденом в начале XX-го века, можно считать одной из разновидностей знаменитого парадокса лжеца.
Филипп Журден
Представьте себе — вы держите в руках открытку, на которой написано: «Утверждение на обратной стороне открытки истинно». Перевернув открытку, вы обнаруживаете фразу «Утверждение на другой стороне ложно». Как вы понимаете, противоречие налицо: если первое утверждение правдиво, то второе тоже соответствует действительности, но в таком случае первое должно оказаться ложным. Если же первая сторона открытки лжива, то фразу на второй также нельзя считать истинной, а это значит, первое утверждение опять-таки становится правдой… Ещё более интересный вариант парадокса лжеца — в следующем пункте.
5. Софизм «Крокодил»
На берегу реки стоят мать с ребёнком, вдруг к ним подплывает крокодил и затаскивает ребёнка в воду. Безутешная мать просит вернуть её чадо, на что крокодил отвечает, что согласен отдать его целым и невредимым, если женщина правильно ответит на его вопрос: «Вернёт ли он её ребёнка?». Понятно, что у женщины два варианта ответа — да или нет. Если она утверждает, что крокодил отдаст ей ребёнка, то всё зависит от животного — посчитав ответ правдой, похититель отпустит ребёнка, если же он скажет, что мать ошиблась, то ребёнка ей не видать, согласно всем правилам договора.
© Коракс Сиракузский
Отрицательный ответ женщины всё значительно усложняет — если он оказывается верным, похититель должен выполнить условия сделки и отпустить дитя, но таким образом ответ матери не будет соответствовать действительности. Чтобы обеспечить лживость такого ответа, крокодилу нужно вернуть ребёнка матери, но это противоречит договору, ведь её ошибка должна оставить чадо у крокодила.
Стоит отметить, что сделка, предложенная крокодилом, содержит логическое противоречие, поэтому его обещание невыполнимо. Автором этого классического софизма считается оратор, мыслитель и политический деятель Коракс Сиракузский, живший в V-м веке до нашей эры.
6. Апория «Дихотомия»
© www.student31.ru
Ещё один парадокс от Зенона Элейского, демонстрирующий некорректность идеализированной математической модели движения. Проблему можно поставить так — скажем, вы задались целью пройти какую-нибудь улицу вашего города от начала и до конца. Для этого вам необходимо преодолеть первую её половину, затем половину оставшейся половины, далее половину следующего отрезка и так далее. Иначе говоря — вы проходите половину всего расстояния, затем четверть, одну восьмую, одну шестнадцатую — количество уменьшающихся отрезков пути стремится к бесконечности, так как любую оставшуюся часть можно разделить надвое, значит пройти весь путь целиком невозможно. Формулируя несколько надуманный на первый взгляд парадокс, Зенон хотел показать, что математические законы противоречат реальности, ведь на самом деле вы можете без труда пройти всё расстояние без остатка.
7. Апория «Летящая стрела»
Знаменитый парадокс Зенона Элейского затрагивает глубочайшие противоречия в представлениях учёных о природе движения и времени. Апория сформулирована так: стрела, выпущенная из лука, остаётся неподвижной, так как в любой момент времени она покоится, не совершая перемещения. Если в каждый момент времени стрела покоится, значит она всегда находится в состоянии покоя и не движется вообще, так как нет момента времени, в который стрела перемещается в пространстве.
© www.academic.ru
Выдающиеся умы человечества веками пытаются разрешить парадокс летящей стрелы, однако с логической точки зрения он составлен абсолютно верно. Для его опровержения требуется объяснить, каким образом конечный временной отрезок может состоять из бесконечного числа моментов времени — доказать это не удалось даже Аристотелю, убедительно критиковавшему апорию Зенона. Аристотель справедливо указывал, что отрезок времени нельзя считать суммой неких неделимых изолированных моментов, однако многие учёные считают, что его подход не отличается глубиной и не опровергает наличие парадокса. Стоит отметить, что постановкой проблемы летящей стрелы Зенон стремился не опровергнуть возможность движения, как таковую, а выявить противоречия в идеалистических математических концепциях.
8. Парадокс Галилея
Галилео Галилей / © Wikimedia
В своём труде «Беседы и математические доказательства, касающиеся двух новых отраслей науки» Галилео Галилей предложил парадокс, демонстрирующий любопытные свойства бесконечных множеств. Учёный сформулировал два противоречащих друг другу суждения. Первое: есть числа, представляющие собой квадраты других целых чисел, например 1, 9, 16, 25, 36 и так далее. Существуют и другие числа, у которых нет этого свойства — 2, 3, 5, 6, 7, 8, 10 и тому подобные. Таким образом, общее количество точных квадратов и обычных чисел должно быть больше, чем количество только точных квадратов. Второе суждение: для каждого натурального числа найдётся его точный квадрат, а для каждого квадрата существует целый квадратный корень, то есть, количество квадратов равно количеству натуральных чисел.
На основании этого противоречия Галилей сделал вывод, что рассуждения о количестве элементов применены только к конечным множествам, хотя позже математики ввели понятие, мощности множества — с его помощью была доказана верность второго суждения Галилея и для бесконечных множеств.
9. Парадокс мешка картофеля
© nieidealne-danie.blogspot.com
Допустим, у некоего фермера имеется мешок картофеля весом ровно 100 кг. Изучив его содержимое, фермер обнаруживает, что мешок хранился в сырости — 99% его массы составляет вода и 1% остальные вещества, содержащиеся в картофеле. Он решает немного высушить картофель, чтобы содержание воды в нём снизилось до 98% и переносит мешок в сухое место. На следующий день оказывается, что, один литр (1 кг) воды действительно испарился, но вес мешка уменьшился со 100 до 50 кг, как такое может быть? Давайте посчитаем — 99% от 100 кг это 99 кг, значит соотношение массы сухого остатка и массы воды изначально было равно 1/99. После сушки вода насчитывает 98% от общей массы мешка, значит соотношение массы сухого остатка к массе воды теперь составляет 1/49. Так как масса остатка не изменилась, оставшаяся вода весит 49 кг.
Конечно, внимательный читатель сразу обнаружит грубейшую математическую ошибку в расчётах — мнимый шуточный «парадокс мешка картофеля» можно считать отличным примером того, как с помощью на первый взгляд «логичных» и «научно подкреплённых» рассуждений можно буквально на пустом месте выстроить теорию, противоречащую здравому смыслу.
10. Парадокс воронов
Карл Густав Гемпель / © Wikimedia
Проблема также известна, как парадокс Гемпеля — второе название она получила в честь немецкого математика Карла Густава Гемпеля, автора её классического варианта. Проблема формулируется довольно просто: каждый ворон имеет чёрный цвет. Из этого следует, что всё, что не чёрного цвета, не может быть вороном. Этот закон называется логическая контрапозиция, то есть если некая посылка «А» имеет следствие «Б», то отрицание «Б» равнозначно отрицанию «А». Если человек видит чёрного ворона, это укрепляет его уверенность, что все вороны имеют чёрный окрас, что вполне логично, однако в соответствии с контрапозицией и принципом индукции, закономерно утверждать, что наблюдение предметов не чёрного цвета (скажем, красных яблок) также доказывает, что все вороны окрашены в чёрный цвет. Иными словами — то, что человек живёт в Санкт-Петербурге доказывает, что он живёт не в Москве.
С точки зрения логики парадокс выглядит безукоризненно, однако он противоречит реальной жизни — красные яблоки никоим образом не могут подтверждать тот факт, что все вороны чёрного цвета.
15 парадоксов, которые взорвут ваш мозг :: Инфониак
 Невероятные факты
Невероятные факты
Я знаю, что ничего не знаю. Так сказал однажды Сократ.
Это заявление само по себе парадоксально, потому как демонстрирует сложность значения одного слова.
Также оно объясняет понимание видения мира одним из основателей западной философии: вы должны подвергать сомнению всё, что вы думаете, что знаете.
Действительно, чем глубже копать, тем больше парадоксов вокруг вы начнёте видеть.
1. Чтобы дойти куда-либо, вы должны сначала пройти полпути, затем пройти половину из оставшейся половины, потом ещё половину оставшегося расстояния и так до бесконечности: таким образом, движение невозможно.
Парадокс дихотомии считается детищем древнегреческого философа Зенона, который якобы был создан для доказательства того, что Вселенная уникальна и что любое изменение, включая движение, невозможно (такого же мнения придерживался и его учитель Парменид).
Люди интуитивно отвергают этот парадокс на протяжении уже многих лет.
С математической точки зрения решение, к которому пришли ещё в 19 веке, состоит в том, чтобы принять, что половина плюс одна четверть плюс одна восьмая плюс одна шестнадцатая и так далее вплоть до одного. Это похоже на число 0,999…., которое когда-то станет 1.
Но данное теоретическое решение на самом деле не объясняет, как именно объект достигает пункта назначения. Решение этого вопроса более сложное и до сих пор не ясное, учитывая теории 20 века о материи, времени и пространстве, которые неделимы.
2. В любой момент движущийся объект неотличим от неподвижного, поэтому движение невозможно.
Это парадокс называется парадоксом стрелы, и это ещё один аргумент Зенона против движения. Проблема здесь в том, что в один момент времени проходит 0 секунд, и поэтому движение в данном случае нулевое.
Читайте также: 12 невероятных парадоксов
Зенон утверждал, что если бы время было составлено из мгновений, то тот факт, что движение не происходит в какой-то конкретный момент, говорил бы о том, что оно не происходит вообще.
Как и парадокс дихотомии, парадокс стрелы фактически намекает на современные представления о квантовой механики. В книге «Размышления об относительности» («Reflections of Relativity») Кевин Браун отмечает, что в контексте специальной теории относительности объект в движении отличается от неподвижного объекта.
Относительность требует, чтобы объекты, движущиеся с различной скоростью, по-разному представлялись стороннему наблюдателю, а также, чтобы они сами по себе имели различные преставления об окружающем мире.
Интересные парадоксы
3. Если вы восстановили корабль, заменив все его деревянные части, это остался тот же корабль?
Ещё один классический парадокс из Древней Греции, «Корабль Тесея» — это парадокс о противоречиях идентичности. Его хорошо описал Плутарх.
Корабль, на котором Тесей и молодёжь Афин возвращались с Крита, имел 30 весёл, которые были сохранены вплоть до времён Димитрия Фалерея. А всё благодаря тому, что когда старые деревянные доски начали разлагаться, их заменили на новые, более крепкие.
Они держались так долго, что этот корабль стал постоянной темой обсуждения среди философов, которые говорили о логике разных вещей, которые изменяются. Одна группа философов говорила, что корабль остался тем же, в то время, как другие философы настаивали, что после замены брёвен, корабль стал другим.
4. Может ли Всемогущий создать скалу, слишком тяжёлую для того, чтобы он сам мог её поднять?
Как может существовать зло, если Бог всемогущ? Как можем мы называть себя свободными, если Бог всеведущ?
Это лишь несколько из многих существующих парадоксов, касающихся применения вопросов логики к божественной теме.
Читайте также: 20 жизненных парадоксов, которые сделают вас мудрее
Некоторые люди могут ссылаться на эти парадоксы, объясняя тем самым, почему они не верят в высшее существо. Однако, другие говорят, что они несущественны и по разным причинам не работают.
Удивительные парадоксы
5. Существует бесконечно длинный «рог», которые имеет конечный объём, но бесконечную площадь поверхности.
Двигаясь навстречу проблеме, появившейся в 17 веке, мы получаем один из многих парадоксов, связанных с геометрией и бесконечностью.
«Рог Гавриила» формируется путём взятия кривой y = 1/х и поворота вокруг горизонтальной оси, как показано на рисунке.
Используя методы исчисления, которые позволяют вычислить площади и объёмы построенных таким образом фигур, можно видеть, что бесконечно длинный рог фактически имеет конечный объём, равный числу пи, но бесконечную площадь поверхности.
Иными словами, в рог поместится определённое количество краски, но для того, чтобы покрыть краской всю его поверхность, потребуется её бесконечное количество.
6. Гетерологическое слово – это слово, которое не описывает себя. А описывает ли себя слово «гетерологический»?
Это один из многих парадоксов, который долго томил умы современных математиков и логиков.
Примером гетерологического слова может быть слово «глагол», которое не является глаголом по сути (в отличие от «существительного», которое является существительным). Другим примером может быть слово «длинный», которое не является длинным словом (в отличие от слова «короткий», которое является коротким словом).
Так «гетерологический» является гетеролигическим словом или нет? Если бы это было бы слово, которое не описывает себя, тогда оно бы описывало себя. А если бы оно было словом, которое описывает себя, оно бы не описывало себя.
Это связано с парадоксом Рассела, который спрашивает, содержит ли определённое множество себя в качестве элемента.
Читайте также: 10 необычных мысленных экспериментов
Создавая подобные самоуничтожающиеся множества, Бертран Рассел (Bertrand Russell) и другие учёные продемонстрировали важность установления тщательных правил при создании множеств, которые заложили основу математики 20 века.
Самые невероятные парадоксы
7. Пилоты могут «выйти» из боевого режима, если они психологически непригодны, но каждый, кто хочет «выйти» из боевого дежурства, доказывает, что он нормален.
«Уловка -22» — это сатирический роман о Второй мировой войне Джозефа Хеллера (Joseph Heller), в котором описывается ситуация, когда кто-то нуждается в чём-то, что можно получить только тогда, когда он в этом не нуждается.
Это так называемый парадокс саморефенеции. Главный герой романа Йоссариан столкнулся с этим парадоксом при оценке пилотной деятельности, но в итоге, куда бы он направлялся, он везде видел парадоксальные и репрессивные правила.
8. В каждой цифре есть что-то интересное.
1 – это первое ненулевое натуральное число, 2 – наименьшее простое число, 3 – первое нечётное простое число, 4 – наименьшее составное число и т.д. Когда вы наконец доберетесь до числа, которое покажется вам неинтересным, то это число окажется интересным из-за того, что оно показалось вам неинтересным.
Парадокс интересного числа основан на неточном определении слова «интересный», что делает его несколько более глупым вариантом гетерологического парадокса и парадокса Рассела, которые полагаются на противоречивые самореференции.
Исследователь квантовых вычислений Натаниэль Джонстон (Nathaniel Johnston) нашёл умное решение парадокса. Вместо того, чтобы полагаться на интуитивное понятие слова «интересно», как в исходном парадоксе, он определил интересное целое число как таковое, появляющееся в онлайн энциклопедии целочисленных последовательностей.
Читайте также: 10 самых пугающих теорий, известных человеку
А это наборы из десятков тысяч математических последовательностей, таких как простые числа, числа Фибоначчи, пифагорейские тройки и т.д.
Исходя из этого определения, первое неинтересное число, наименьшее целое число, которое не отображалось ни в одной из последовательностей, — 11 630. Так как в энциклопедию на постоянной основе добавляются новые последовательности, некоторые из них включают в себя бывшие ранее неинтересными цифры.
Самые интересные парадоксы
9. В баре всегда есть хотя бы один клиент, для которого верно, что если пьёт он, значит пьют все.
Условные утверждения в формальной логике иногда имеют противоречивые интерпретации, а парадокс пьянства – отличный тому пример. На первый взгляд, парадокс предполагает, что один человек заставляет пить остальную часть бара.
Фактически всё это говорит о том, что было бы невозможно, чтобы все в баре пили, если бы каждый отдельно взятый клиент не пил. Поэтому там есть по крайней мере один клиент (то есть последний, который не пьёт), который выпив, мог бы сделать так, чтобы можно было сказать, что пьют все.
10. Из мяча, который можно разрезать на конечное число частей, реально сделать два других мяча одинакового размера.
Парадокс Банаха-Тарского опирается на множество странных и противоречивых свойств бесконечных множеств и геометрических вращений.
Читайте также: 10 причин, по которым мы до сих пор не нашли инопланетян
Части, на которые можно разрезать мяч, будут выглядеть очень странно, поэтому парадокс работает только в абстрактной математической сфере. Было бы отлично, если можно было взять, к примеру, яблоко, разрезать его на части и собрать два одинаковых, но меньшего размера, чтобы поделиться с другом.
Но физические «шары» из материального мира не могут быть разобраны как математическая сфера.
Странные парадоксы
11. Картофель весом в 100 граммов – это 99 процентов воды. Если он высохнет на 1 процент, то его новый вес составит 50 граммов.
Даже при работе по устаревшим методам с конечными величинами, математика может привести к странным результатам.
Чтобы понять картофельный парадокс, нужно внимательно взглянуть на количество содержащейся в картофеле воды.
Поскольку картошка на 99 процентов – это вода, то сухие компоненты получается равны 1 проценту. Вес картофеля – 100 граммов, следовательно, вес сухого материала – 1 грамм.
Когда 100 граммов картофеля высушивается до 98 процентов воды, то 1 грамм сухого компонента превращается в 2 грамма. А один грамм – это два процента от 50 граммов, таким и должен быть новый вес картофелины.
12. Если в комнате находятся 23 человека, очень высоки шансы, что, как минимум, двое из них родились в один и тот же день.
Ещё один удивительный математический результат: парадокс дня рождения исходит из тщательного анализа связанных с этим вероятностей.
Если в комнате находятся два человека, то вероятность того, что у них день рождения в один и тот же день, равна 1/365 (без учёта високосных лет), потому как помимо дня рождения одного человека, в году есть ещё 364 других дня, любой из которых может быть днём рождения второго человека.
Если в комнате три человека, то вероятность того, что у них у всех разные дни рождения равна 364/365 x 363/365. То есть когда мы знаем день рождения первого человека, на выбор даты рождения второго остаётся 364 дня, а для третьего – 363 дня.
Читайте также: Возможны ли путешествия во времени?
Продолжая таким образом, мы доходим до количества в 23 человека, и обнаруживаем, что вероятность того, что у всех людей будут разные дни рождения опускается ниже 50 процентов, поэтому вероятность двух одинаковых дней рождения существенно повышается.
13. У друзей большинства людей больше друзей, чем у них самих.
Это кажется невозможным, но когда вы смотрите на вопрос с математической точки зрения, всё становится понятно. Наглядным примером данного парадокса служат социальные сети, в которых у большинства людей мало друзей. Но некоторые из них – это очень общительные люди, поэтому друзей у них очень много.
Эти люди очень часто «показываются» в качестве «друзей моих друзей», поэтому они и поднимают среднее их количество.
14. Физик, занимающийся изобретением машины времени, посещает «старую» версию себя. Эта «версия» даёт ему идеи по созданию машины времени, а «молодая» версия использует эти идеи для создания непосредственно аппарата, со времени возвращаясь к старой версии себя.
Путешествие во времени, если это будет возможно, может привести к очень странным ситуациям.
Парадокс Бутстрапа – это противоположность классического парадокса дедушки. Для того, чтобы вернуться назад и не позволить себе путешествовать во времени, некоторая информация и объекты возвращаются во времени, и дают возможность позже вернуться молодой версии себя.
И тут появляется вопрос: каким образом в первый раз появились эта информация и объект. Данный парадокс обсуждали еще в 1941 году. Роберт Хайнлайн (Robert Heinlein) был одним из первых, кто поднял эту тему.
Использование данного парадокса – это не редкость в научной фантастике, а своё название парадокс взял как раз из рассказа Роберта Хайнлайна.
15. Если на Земле нет ничего уникального, тогда в нашей галактике должно существовать много инопланетных цивилизаций. Однако, люди пока не нашли доказательства наличия другой разумной жизни во Вселенной.
Некоторые люди считают молчание нашей Вселенной парадоксом. Одно из основополагающих предположений астрономии: планета Земля – это довольно обычная планета с общей солнечной системой в общей галактике, которая не является чем-то космически уникальным.
Спутник NASA обнаружил, что в нашей галактике, вероятно, есть около 11 миллиардов подобных Земле планет. Учитывая это, жизнь, подобная нам, должна была развиться где-то не слишком далеко от нас (по крайней мере, в космическом масштабе).
Но несмотря на существование мощнейших телескопов, люди не смогли обнаружить существование ни одной технологической цивилизации нигде во Вселенной. Цивилизации шумны: человечество транслирует телевизионные и радиосигналы, которые однозначно искусственны.
Такая цивилизация, как наша, должна давать признаки своего существования, которые люди бы нашли, если бы они существовали.
Более того, цивилизация, возникшая миллионы лет назад (довольно недавно с космической точки зрения), имела достаточно времени для того, чтобы хотя бы начать колонизировать галактику, а это означает, что свидетельств её существования должно быть ещё больше.
Действительно, имея в распоряжении такое количество времени, колонизирующая цивилизация смогла бы колонизировать всю Галактику. Физик Энрико Ферми (Enrico Fermi), в честь которого был назван этот парадокс, как-то во время обеденного перерыва с коллегами спросил: «Где они?»
Одно из решений парадокса бросает вызов вышеизложенной идее и говорит о том, что сложные жизни – это крайне редкая вещь во Вселенной. Другая теория утверждает, что технологические цивилизации неизбежно уничтожаются в результате ядерной войны или экологического разрушения.
Более оптимистичным решением является идея о том, что инопланетяне намеренно скрываются от нас, пока мы не станем более социально и технологически зрелыми. Ещё одна теория гласит, что чужеродные технологии настолько развиты, что мы даже не можем их распознать.
12 невероятных парадоксов :: Инфониак
 Невероятные факты
Невероятные факты
Парадоксы существовали со времен древних греков. При помощи логики можно быстро найти фатальный недостаток в парадоксе, который и показывает, почему, казалось бы невозможное, возможно или что весь парадокс просто построен на недостатках мышления.
А вы сможете понять, в чем недостаток каждого из ниже перечисленных парадоксов?
Парадоксы пространства
12. Парадокс Ольберса
В астрофизике и физической космологии парадокс Ольберса – это аргумент, говорящий о том, что темнота ночного неба конфликтует с предположением о бесконечной и вечной статической Вселенной. Это одно из свидетельств нестатической Вселенной, такое как текущая модель Большого взрыва. Об этом аргументе часто говорят как о «темном парадоксе ночного неба», который гласит, что под любым углом зрения с земли линия видимости закончится, достигнув звезды.
© snezhanna / Getty Images
Чтобы понять это, мы сравним парадокс с нахождением человека в лесу среди белых деревьев. Если с любой точки зрения линия видимости заканчивается на верхушках деревьев, человек разве продолжает видеть только белый цвет? Это противоречит темноте ночного неба и заставляет многих людей задаться вопросом, почему мы не видим только свет от звезд в ночном небе.
11. Парадокс всемогущества
Парадокс состоит в том, что если существо может выполнять какие-либо действия, то оно может ограничить свою способность выполнять их, следовательно, оно не может выполнять все действия, но, с другой стороны, если оно не может ограничивать свои действия, то это что-то, что оно не может сделать.
Это, судя по всему, подразумевает, что способность всемогущего существа ограничивать себя обязательно означает, что оно действительно ограничивает себя. Этот парадокс часто формулируется в терминологии авраамических религий, хотя это и не является обязательным требованием.
Одна из версий парадокса всемогущества заключается в так называемом парадоксе о камне: может ли всемогущее существо создать настолько тяжелый камень, что даже оно будет не в состоянии поднять его? Если это так, то существо перестает быть всемогущим, а если нет, то существо не было всемогущим с самого начала.
Ответ на парадокс заключается в следующем: наличие слабости, такой как невозможность поднять тяжелый камень, не попадает под категорию всемогущества, хотя определение всемогущества подразумевает отсутствие слабостей.
10. Парадокс Сорита
Парадокс состоит в следующем: рассмотрим кучу песка, из которого постепенно удаляются песчинки. Можно построить рассуждение, используя утверждения:
— 1000000 песчинок – это куча песка
— куча песка минус одна песчинка – это по-прежнему куча песка.
© ninoninos / Getty Images
Если без остановки продолжать второе действие, то, в конечном счете, это приведет к тому, что куча будет состоять из одной песчинки. На первый взгляд, есть несколько способов избежать этого заключения. Можно возразить первой предпосылке, сказав, что миллион песчинок – это не куча. Но вместо 1000000 может быть сколь угодно другое большое число, а второе утверждение будет верным при любом числе с любым количеством нулей.
Таким образом, ответ должен прямо отрицать существование таких вещей, как куча. Кроме того, кто-то может возразить второй предпосылке, заявив, что она верна не для всех «коллекций зерна» и что удаление одного зерна или песчинки все еще оставляет кучу кучей. Или же может заявить о том, что куча песка может состоять из одной песчинки.
9. Парадокс интересных чисел
Утверждение: не такого понятия, как неинтересное натуральное число.
Доказательство от противного: предположим, что у вас есть непустое множество натуральных чисел, которые неинтересны. Благодаря свойствам натуральных чисел, в перечне неинтересных чисел обязательно будет наименьшее число.
© stephankarg
Будучи наименьшим числом множества его можно было бы определить как интересное в этом наборе неинтересных чисел. Но так как изначально все числа множества были определены как неинтересные, то мы пришли к противоречию, так как наименьшее число не может быть одновременно и интересным, и неинтересным. Поэтому множества неинтересных чисел должны быть пустыми, доказывая, что не существует такого понятия, как неинтересные числа.
8. Парадокс летящей стрелы
Данный парадокс говорит о том, что для того, чтобы произошло движение, объект должен изменить позицию, которую он занимает. В пример приводится движение стрелы. В любой момент времени летящая стрела остается неподвижной, потому как она покоится, а так как она покоится в любой момент времени, значит, она неподвижна всегда.
© Oleksandr Bushko / Getty Images
То есть данный парадокс, выдвинутый Зеноном еще в 6 веке, говорит об отсутствии движения как таковом, основываясь на том, что двигающееся тело должно дойти до половины, прежде чем завершить движение. Но так как оно в каждый момент времени неподвижно, оно не может дойти до половины. Этот парадокс также известен как парадокс Флетчера.
Стоит отметить, что если предыдущие парадоксы говорили о пространстве, то следующая апория – о делении времени не на сегменты, а на точки.
Парадокс времени
7. Апория «Ахиллес и черепаха»
Прежде, чем разъяснить, в чём суть «Ахиллеса и черепахи» важно отметить, что это утверждение является апорией, а не парадоксом. Апория – это логически верная ситуация, но вымышленная, которая в реальности не может существовать.
Парадокс же, в свою очередь, — это ситуация, которая может существовать в действительности, но не имеет логического объяснения.
Таким образом, в данной апории Ахиллес бежит за черепахой, предварительно дав ей фору в 30 метров. Если предположить, что каждый из бегунов начал бежать с определенной постоянной скоростью (один очень быстро, второй очень медленно), то через некоторое время Ахиллес, пробежав 30 метров, достигнет той точки, от которой двинулась черепаха. За это время черепаха «пробежит» гораздо меньше, скажем, 1 метр.
Затем Ахиллесу потребуется еще какое-то время, чтобы преодолеть это расстояние, за которое черепаха продвинется еще дальше. Достигнув третьей точки, в которой побывала черепаха, Ахиллес продвинется дальше, но все равно не нагонит ее. Таким образом, всякий раз, когда Ахиллес будет достигать черепаху, она все равно будет впереди.
Таким образом, поскольку существует бесконечное количество точек, которых Ахиллес должен достигнуть, и в которых черепаха уже побывала, он никогда не сможет догнать черепаху. Конечно, логика говорит нам о том, что Ахиллес может догнать черепаху, потому это и является апорией.
Проблема этой апории заключается в том, что в физической реальности невозможно бесконечно пересекать поперечно точки – как вы можете попасть из одной точки бесконечности в другую, не пересекая при этом бесконечность точек? Вы не можете, то есть, это невозможно.
Но в математике это не так. Эта апория показывает нам, как математика может что-то доказать, но в действительности это не работает. Таким образом, проблема данной апории в том, что происходит применение математических правил для нематематических ситуаций, что и делает её неработающей.
6. Парадокс Буриданова осла
Это образное описание человеческой нерешительности. Это относится к парадоксальной ситуации, когда осел, находясь между двумя абсолютно одинаковыми по размеру и качеству стогами сена, будет голодать до смерти, поскольку так и не сможет принять рациональное решение и начать есть.
Парадокс назван в честь французского философа 14 века Жана Буридана (Jean Buridan), однако, он не был автором парадокса. Он был известен еще со времен Аристотеля, который в одном из своих трудов рассказывает о человеке, который был голоден и хотел пить, но так как оба чувства были одинаково сильны, а человек находился между едой и питьем, он так и не смог сделать выбора.
© homermi / Getty Images Pro
Буридан, в свою очередь, никогда не говорил о данной проблеме, но затрагивал вопросы о моральном детерминизме, который подразумевал, что человек, столкнувшись с проблемой выбора, безусловно, должен выбирать в сторону большего добра, но Буридан допустил возможность замедления выбора с целью оценки всех возможных преимуществ. Позднее другие авторы отнеслись с сатирой к этой точке зрения, говоря об осле, который столкнувшись с двумя одинаковыми стогами сена, будет голодать, принимая решение.
5. Парадокс неожиданной казни
Судья говорит осужденному, что он будет повешен в полдень в один из рабочих дней на следующей неделе, но день казни будет для заключенного сюрпризом. Он не будет знать точную дату, пока палач в полдень не придет к нему в камеру. После, немного порассуждав, преступник приходит к выводу, что он сможет избежать казни.
© konstantin32 / Getty Images
Его рассуждения можно разделить на несколько частей. Начинает он с того, что его не могут повесить в пятницу, так как если его не повесят в четверг, то пятница уже не будет неожиданностью. Таким образом, пятницу он исключил. Но тогда, так как пятница уже вычеркнута из списка, он пришел к выводу, что он не может быть повешенным и в четверг, потому что если его не повесят в среду, то четверг тоже не будет неожиданностью.
Рассуждая аналогичным образом, он последовательно исключил все оставшиеся дни недели. Радостным он ложится спать с уверенностью, что казни не произойдет вовсе. На следующей неделе в полдень среды к нему в камеру пришел палач, поэтому, несмотря на все его рассуждения, он был крайне удивлен. Все, что сказал судья, сбылось.
4. Парадокс парикмахера
Предположим, что существует город с одним мужским парикмахером, и что каждый мужчина в городе бреется налысо: некоторые самостоятельно, некоторые с помощью парикмахера. Кажется разумным предположить, что процесс подчиняется следующему правилу: парикмахер бреет всех мужчин и только тех, кто не бреется сам.
© Oleg Baliuk
Согласно этому сценарию, мы можем задать следующий вопрос: парикмахер бреет себя сам? Однако, спрашивая это, мы понимаем, что ответить на него правильно невозможно:
— если парикмахер не бреется сам, он должен соблюдать правила и брить себя сам;
— если он бреет себя сам, то по тем же правилам он не должен брить себя сам.
3. Парадокс Эпименида
Этот парадокс вытекает из заявления, в котором Эпименид , противореча общему убеждению Крита, предположил, что Зевс был бессмертным, как в следующем стихотворении:
Они создали гробницу для тебя, высший святой
Критяне, вечные лжецы, злые звери, рабы живота!
Но ты не умер: ты жив и будешь жив всегда,
Ибо ты живешь в нас, а мы существуем.
Тем не менее, он не осознавал, что называя всех критян лжецами, он невольно и самого себя называл обманщиком, хотя он и «подразумевал», что все критяне, кроме него. Таким образом, если верить его утверждению, и все критяне лжецы на самом деле, он тоже лжец, а если он лжец, то все критяне говорят правду. Итак, если все критяне говорят правду, то и он в том числе, а это означает, исходя из его стиха, что все критяне лжецы. Таким образом, цепочка рассуждений возвращается в начало.
2. Парадокс Эватла
Это очень старая задача в логике, вытекающая из Древней Греции. Говорят, что знаменитый софист Протагор взял к себе на учение Эватла, при этом, он четко понимал, что ученик сможет заплатить учителю только после того, как он выиграет свое первое дело в суде.
Некоторые эксперты утверждают, что Протагор потребовал деньги за обучение сразу же после того, как Эватл закончил свою учебу, другие говорят, что Протагор подождал некоторое время, пока не стало очевидно, что ученик не прикладывает никаких усилий для того, чтобы найти клиентов, третьи же уверены в том, что Эватл очень старался, но клиентов так и не нашел. В любом случае, Протагор решил подать в суд на Эватла, чтобы тот вернул долг.
© Markus Spiske temporausch.com / Pexels
Протагор утверждал, что если он выиграет дело, то ему будут выплачены его деньги. Если бы дело выиграл Эватл, то Протагор по-прежнему должен был получить свои деньги в соответствии с первоначальным договором, потому что это было бы первое выигрышное дело Эватла.
Эватл, однако, стоял на том, что если он выиграет, то по решению суда ему не придется платить Протагору. Если, с другой стороны, Протагор выиграет, то Эватл проигрывает свое первое дело, поэтому и не должен ничего платить. Так кто же из мужчин прав?
1. Парадокс непреодолимой силы
Парадокс непреодолимой силы представляет собой классический парадокс, сформулированный как «что происходит, когда непреодолимая сила встречает неподвижный объект?» Парадокс следует воспринимать как логическое упражнение, а не как постулирование возможной реальности.
© Mikosch / Getty Images
Согласно современным научным пониманиям, никакая сила не является полностью неотразимой, и не существует и быть не может полностью недвижимых объектов, так как даже незначительная сила будет вызывать небольшое ускорение объекта любой массы. Неподвижный предмет должен иметь бесконечную инерцию, а, следовательно, и бесконечную массу. Такой объект будет сжиматься под действием собственной силы тяжести. Непреодолимой силе потребуется бесконечная энергия, которая не существует в конечной Вселенной.
В мире математических парадоксов / Хабр
Доброго времени суток, уважаемое хабрасообщество.
Сегодня я хотел бы затронуть такую увлекательную тему, как математические парадоксы. По данной теме на хабре уже было опубликовано несколько замечательных статей (1,2,3,4,5), но в математике интересные парадоксы этой выборкой далеко не исчерпываются.
Поэтому попробуем рассмотреть другие занимательные парадоксы (а некоторые и «не совсем» парадоксы), которые пока еще не получили здесь должного освещения.
Парадокс кучи и парадокс «Лысого»
Данные парадоксы известны еще с древности. Для начала сформулируем и рассмотрим парадокс кучи, связанного с неопределенностью понятия «куча»:
«если к одному зерну добавлять по зёрнышку, то в какой момент образуется куча?»
или обратная формулировка:
«удаляя из кучи в 1 млн зёрен по одному зёрнышку, с какого момента она перестаёт быть кучей?»
Формулировка парадокса основана на очевидной предпосылке, согласно которой одно зёрнышко не образует кучи, и индуктивной предпосылке, по которой добавление одного зернышка к совокупности, кучей не являющейся, несущественно для образования кучи. Из этих предпосылок следует, что никакая совокупность из сколь угодно большого количества зёрен не будет образовывать кучи, что противоречит представлению о существовании кучи из зёрен. Очевидно, что эти рассуждения приводят к неправильным выводам.
Однако до самого недавнего времени не было ясно, какие тогда рассуждения здесь использовать. Лишь с появлением теории нечетких множеств Лофти Заде и нечеткой логики стало ясно, что здесь уместны нечеткие расуждения, поскольку имеется в наличии классический объект нечеткой логики — неопределенное понятие «быть кучей». Данные объекты в нечеткой логике интерпретируются как имеющие неточное значение, характеризуемое некоторым нечётким множеством.
Согласно таким рассуждениям заключение на каждом шаге остается прежним, но принадлежность его правильности уменьшается с каждым шагом. Когда эта принадлежность падает меньше 50%, то более правильным становится противоположное заключение.
Аналогичные рассуждения можно применить и к парадоксу «Лысого»:
«Если волосы с головы выпадают по одному, с какого момента человек становится лысым?»
Парадокс лжеца
Если утверждение на картинке истинно, значит, исходя из его содержания, верно то, что оно — ложно; но если оно — ложно, тогда то, что оно утверждает, неверно; значит, неверно, что утверждение на картинке — ложно, и, значит, это утверждение истинно.
Парадокс лжеца демонстрирует расхождение разговорной речи с формальной логикой, вводя высказывание, которое одновременно и истинно и ложно. В рамках формальной логики данное утверждение не доказуемо и неопровержимо, поэтому решения данного парадокса не существует, но существуют различные варианты его устранения.
Для этого можно применить рассуждения используемые в предыдущем разделе, для этого положим, что утверждение истинно на 0,5, тогда оно и ложно на 0,5, то есть не всякую фразу можно назвать целиком ложной или целиком истинной — «в чем-то высказывание на картинке лжет, а в чем-то — говорит правду»
К такому же выводу можно придти с помощью тройственной логики. В ней есть три степени истинности: «истина», «ложь» и «неопределенно». Под «неопределенно» понимается промежуточное по смыслу значение между истиной и ложью. К данной степени истинности и относят парадокс лжеца.
Как уже говорилось это не решения парадокса лжеца, а всего лишь объяснения, почему данный парадокс возникает в классической двузначной логике высказываний. Они свидетельствует, что строгое деление всех высказываний на истинные и ложные в данном случае неприменимо, поскольку ведет к парадоксу.
В настоящее всемя многие придерживаются такой точки зрения, что данное высказывание вообще не является логическим утверждением, и применять к нему классические методы формальной логики бессмысленно.
Парадокс Тесея
Данный парадокс можно сформулировать следующим образом:
«Если все составные части исходного объекта были заменены, остаётся ли объект тем же объектом?»
Было предложено несколько решений этого парадокса. Согласно философской школе Аристотеля существует несколько описывающих объект причин: форма, материал и суть вещи (которая, по учению Аристотеля, является самой важной характеристикой). Исходя из этого корабль остался тем же, так как его суть не поменялась, лишь изменился износившийся материал.
В следующем решении предложили дать аргументу «тот же» количественную и качественную характеристику. В таком случае, после смены досок корабль Тесея окажется количественно тем же, а качественно — уже другим кораблём.
В последнее время для решения парадокса Тесея предложили использовать 4-х мерную интерпретацию, в которой 3-х мерный корабль имеет также протяженность в 4 измерении-времени. Получившийся 4-х мерный корабль на протяжении временного ряда количественно идентичен с собой. Но отдельные «временные срезы» качественно могут отличаться друг от друга.
Парадокс Абилина
Данный парадокс заключается в том, что группа людей может принять решение, противоречащее возможному выбору любого из членов группы из-за того, что каждый индивидуум считает, что его цели противоречат целям группы, а потому не возражает.
Парадокс был описан Джерри Харви в статье The Abilene Paradox and other Meditations on Management. Имя парадоксу дано по мотивам следующего анекдота, описанного в этой статье:
В один жаркий техасский вечер некая семья играла в домино на крыльце до тех пор, пока тесть не предложил съездить в Абилин отобедать. Жена сказала: «Звучит неплохо». Муж, несмотря на то, что поездка обещала быть долгой и жаркой, подумал, что надо бы подстроиться под других, и произнёс: «По-моему, неплохо; надеюсь, что и твоя мама не откажется». Тёща же ответила: «Конечно, поехали! Я не была в Абилине уже давно».
Дорога была жаркой, пыльной и долгой. Когда же они наконец приехали в кафетерий, еда оказалась невкусной. Спустя четыре часа они, измученные, вернулись домой.Один из них произнёс неискренне: «Верно, неплохая была поездка?». Тёща на это сказала, что, на самом деле, она бы лучше осталась бы дома, но поехала, раз уж остальные трое были полны энтузиазма. Муж сказал: «Я был бы рад никуда не ездить, поехал лишь чтобы доставить остальным удовольствие». Жена произнесла: «А я поехала, рассчитывая на радость остальных. Надо было быть сумасшедшим, чтобы добровольно отправиться в эту поездку». Тесть ответил, что он предложил это лишь потому, что ему показалось, что остальным скучно.
И они сидели, ошеломлённые тем, что поехали в поездку, которой никто из них не хотел. Каждый из них предпочёл бы спокойно наслаждаться тем днём.
Данный парадокс легко объясняется различными социологическими науками, подтверждающими, что человек редко совершает поступки, противоречащие поступкам его группы. Думаю многие не раз сталкивались с данном парадоксом и в своей жизни.
Парадокс Симпсона и феномен Уилла Роджерса
Замечу, что данные парадоксы являются «кажущимися», то есть они могут возникнуть на интуитивном уровне, но если провести вычисления, то легко убедиться, что никакого парадокса не возникает.
Для иллюстрации парадокса Симпсона рассмотрим пример, описанный известным популяризатором математики Мартином Гарднером.
Пусть мы имеем четыре набора камней. Вероятность вытащить чёрный камень набора № 1 выше, чем из набора № 2. В свою очередь, вероятность вытащить чёрный камень из набора № 3 больше, чем из набора № 4. Объединим набор № 1 с набором № 3 (получим набор I), а набор № 2 — с набором № 4 (набор II). Интуитивно можно ожидать, что вероятность вытащить чёрный камень из набора I будет выше, чем из набора II. Однако, в общем случае такое утверждение неверно.
Пример, в котором выполняется парадокс Симпсона:
| Черные шары | Белые шары | Вероятность вытащить черный камень | |
|---|---|---|---|
| Набор №1 | 6 | 7 | 6/13 ≈ 0,4615 |
| Набор №2 | 4 | 5 | 4/9 ≈ 0,4444 |
| Набор №3 | 6 | 3 | 6/9 ≈ 0,6667 |
| Набор №4 | 9 | 5 | 9/14 ≈ 0,6429 |
Теперь смешаем наборы №1 и №3 — из которых черные камни можно вытащить с большей вероятностью и наборы №2 и №4 — из которых черные камни можно вытащить с меньшей вероятностью.
| Черные шары | Белые шары | Вероятность вытащить черный камень | |
|---|---|---|---|
| Набор I | 12 | 10 | 12/22 ≈ 0,5454 |
| Набор II | 13 | 10 | 13/23 ≈ 0,5652 |
Как мы видим из таблицы после смешивания вероятность вытащить черный камень из набора II стала выше чем из набора I.
Математически никакого парадокса тут нет, так как общая вероятность набора зависит от соотношения количества камней черного цвета и обоих цветов, в данном случае в 4 наборе было 9 черных камней, а в первом аж 7 белых, которые больше всего и повлияли на итоговый расклад.
Близок к парадоксу Симпсона и феномен Уилла Роджерса. По сути в них описывается одно и то же явление, но в других терминах.
Думаю многие не раз сталкивались с фразами подобные такой:
«Когда оки покинули Оклахому и переехали в Калифорнию, то повысили средний интеллект обоих штатов»
Эту фразу приписывают Уиллу Роджерсу, в честь чего феномен и получил свое название.
С точки зрения математики никакого парадокса тут тоже нет. Чтобы в этом убедиться достаточно рассмотреть два множества: первое — {1, 2}, а второе — {90,100}, если число 90 из второго множества перенести в первое, то среднее арифметическое элементов как первого множества так и второго повысится.
Исчезновение клетки
Широкий класс задач на перестановку фигур, обладающих признаками софизмов: изначально в их условие введена замаскированная ошибка. В какой-то мере данные задачи ближе к оптическим иллюзиям, чем к математике.
Для примера расмотрим одну подобную задачу: дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка.
Математически парадоксов и таинственного исчезновения площади тут нет. Визуально наблюдаемые треугольники, на самом деле таковымы не являются, гипотенузы в обоих псевдотреугольниках на самом деле являются ломаными линиями (в первом треугольнике она с изломом внутрь, а во втором — наружу). Если наложить треугольник друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «пропавшая» площадь.
Вместо заключения
К моему большому сожалению невозможно рассмотреть все интересные математические парадоксы (и «не совсем» парадоксы) в рамках одной статьи. Но надеюсь, что данная статья не оставила Вас равнодушными, и буду очень рад если Вы решите, что не зря потратили время за чтением.
8 Философские загадки и парадоксы
лотерейный билет Encyclopædia Britannica, Inc.
Вы покупаете лотерейный билет без уважительной причины. Действительно, вы знаете, что шанс выиграть ваш билет составляет не менее 10 миллионов к одному, поскольку по крайней мере 10 миллионов билетов было продано, как вы узнаете позже в вечерних новостях, перед розыгрышем (предположим, что лотерея является честной и что выигрышный билет существует). Таким образом, вы разумно полагаете, что ваш билет потеряет — на самом деле, вы с ума сошли бы, если бы ваш билет выиграл.Точно так же вы вправе полагать, что билет вашей подруги Джейн потеряет, что билет вашего дяди Харви потеряет, что билет вашей собаки Ральфа потеряет, что билет, купленный парнем впереди вас в очереди в магазине, потеряет, и так далее для каждого билета, купленного кем-либо, кого вы знаете или не знаете. В целом, для каждого билета, проданного в лотерее, вы вправе верить: « Этот билет потеряет». Отсюда следует, что вы вправе полагать, что всех билетов потеряет или (что эквивалентно), что ни один билет не выиграет.Но, конечно, вы знаете, что один билет выиграет. Таким образом, вы вправе полагать, что то, что вы знаете, является ложным (что ни один билет не выиграет). Как это может быть?
Лотерея представляет собой очевидный контрпример к одной из версий принципа, известного как дедуктивное закрытие оправдания:
Если человек оправдан в вере в P и оправдан в вере в Q, то он оправдан в вере в любое предположение, которое следует дедуктивно (обязательно) от P и Q.
Например, если я оправдан, полагая, что мой лотерейный билет находится в конверте (потому что я положил его туда), и если я оправдан, полагая, что конверт находится в измельчителе бумаги (потому что я положите его туда), тогда я с полным основанием считаю, что мой лотерейный билет находится в уничтожителе бумаги.
С момента своего появления в начале 1960-х годов парадокс лотереи вызвал много дискуссий о возможных альтернативах принципу закрытия, а также о новых теориях познания и веры, которые сохранили бы этот принцип, избегая при этом его парадоксальных последствий.
парадоксов | Обсуждение философии
Что такое парадокс? Люди используют слово «парадокс» во многих отношениях, например, для обозначения чего-то очень удивительного. Но это не настоящие «философские» парадоксы. В подлинном парадоксе каждый начинает с кажущихся истинными предпосылок, выполняет рассуждения, чтобы получить истинные выводы из истинных предпосылок, и в конечном итоге делает вывод, который, по-видимому, неверен. Вот четыре парадокса:
1. Рассмотрим утверждение «Это утверждение неверно.«Если это правда, то это ложь. Но если это ложь, то это правда. Так что это? Правда? Ложь? Обе? Ни?
2. Чтобы пройти финишную черту, гонщик должен сначала пройти на полпути туда. Но чтобы попасть на полпути, ей сначала нужно пройти четверть пути. Тем не менее, чтобы пройти четверть пути, она должна пройти восьмую часть пути. И так до бесконечности. Но затем, чтобы пройти финишную черту, гонщик должен выполнить бесконечно много задач. И это кажется невозможным, потому что как бы она ни была быстрой, она может делать лишь ограниченное количество вещей в течение своей ограниченной жизни.Так что казалось бы, что гонщик никогда не сможет пройти финишную черту! Но ясно, что она делает. Что дает?
3. Миллион песчинок — это, конечно, куча песка. И, интуитивно, то, что остается после удаления единственного зерна из кучи песка, само по себе является кучей. Но тогда, вопреки интуиции, одна песчинка — это куча! Где это рассуждение не работает? Ложно ли, что миллион песчинок представляет собой кучу? Если так, сколько зерна нужно, чтобы сделать кучу? Или удаление зерна из кучи не всегда дает другую кучу? Если так, то какая наименьшая куча — то есть куча такая, что удаление одного зерна дает не кучу?
4.Пусть RED будет множеством всех красных вещей. Предположительно, RED сам по себе не красный (поскольку наборы, как предполагается, являются бесцветными). Таким образом, RED не является членом самого себя. Пусть СИНИЙ будет набором всех синих вещей. Опять же, СИНИЙ, по-видимому, не синий, и поэтому СИНИЙ не в СИНИЙ. В более общем смысле для каждого качества x пусть X будет множеством всех вещей, которые проявляют x. Теперь рассмотрим множество S, которое содержит КРАСНЫЙ, СИНИЙ и все множества X, которые не являются членами самих себя. S в S или нет? Если это так, то S не является членом самого себя.Если это не так, то S является членом самого себя. Оба результата абсурдны! Но приведенные рассуждения казались совершенно ясными и обоснованными. Что это говорит нам о наших методах аргументации и наших представлениях о качестве, множестве и так далее?
С гостем Роем Соренсеном из Дартмутского колледжа Джон и Кен обсуждают эти и другие парадоксы. Являются ли они неразрешимыми или исчезают, когда кто-то задумывается о них достаточно глубоко? И так или иначе, они имеют теоретическое или практическое значение, или они просто сногсшибательны?
- Обоснованный философский отчет (поиск в 5:55): Зои Корнели берет интервью у Пало Манкузо из Калифорнийского университета в Беркли об истории парадокса Рассела, обрисованной в общих чертах в (4) выше.История вращается вокруг Готтлоба Фреге, непопулярного и амбициозного немецкого математика, который в конце девятнадцатого века пытался свести всю математику к логике, и Бертрана Рассела, молодого и аристократического английского философа, который обнаружил роковой недостаток в попытке сокращения Фреге.
- 60-секундный философ (ищите 49:35): В этом взгляде на «философию парадокса» Джо Ханта, Ян Шоллс показывает, насколько искаженными могут стать популярные представления о парадоксе.Хант, когда-то руководивший знаменитой схемой Ponzi под названием Billionaire Boys Club и теперь отбывая пожизненное заключение за убийство, считал, что что-то зависит от того, как вы на это смотрите, и что ничто не реально, кроме того, что вы хотите. После «случайного» убийства мошенника, который якобы обманул миллионы из Клуба, Хант даже зашел так далеко, что отрицал, что этот человек мертв! Парадоксально? Вам решать.
.
парадоксов Зенона | Греческая философия
Парадоксы Зенона , высказывания греческого философа Зенона Элеа, ученика Парменида 5-го века до нашей эры, призванного показать, что любое утверждение, противоположное монистическому учению Парменида, приводит к противоречию и абсурд. Парменид утверждал только по одной причине, что утверждение, что только Бытие есть , приводит к выводам, что Бытие (или все, что есть) является (1) единым и (2) неподвижным.Противоположные утверждения, таким образом, заключаются в том, что вместо единого Существа существует множество реальных сущностей, и что они находятся в движении (или могли бы быть). Таким образом, Зенон хотел довести до абсурда два утверждения: (1), что многие есть, и (2) это движение.
Подробнее на эту тему
Элеатизм: парадоксы Зенона
Позиция другого великого ученика Парменида, Зенона Элеа, была четко изложена в первой части диалога Платона «Парменид»….
Диалог Платона, Парменид, — лучший источник общего намерения Зенона, и Платон подтвердил мнение других древних авторов. Платон ссылался только на проблему многих, и он не предоставил подробностей. Аристотель, с другой стороны, дал краткие изложения аргументов Зенона о движении; и это, знаменитые и противоречивые парадоксы, как правило, идут по именам, извлеченным из рассказа Аристотеля: Ахилл (или Ахилл и черепаха), дихотомия, стрела и стадион.
Парадокс Ахилла разработан, чтобы доказать, что более медленный двигатель никогда не будет проходить быстрее в гонке. Парадокс дихотомии призван доказать, что объект никогда не достигает конца. Любой движущийся объект должен достигнуть половины пути, прежде чем он достигнет конца; и поскольку существует бесконечное количество промежуточных точек, движущийся объект никогда не достигает конца за конечное время. Парадокс стрелы стремится доказать, что движущийся объект действительно находится в покое. Парадокс стадиона пытается доказать, что из двух наборов объектов, движущихся с одинаковой скоростью, один будет проходить вдвое дальше, чем другой в одно и то же время.
Если в каждом случае заключение кажется необходимым, но абсурдным, оно служит для опровержения предпосылки (это движение существует или реально), и это предполагает, что противоречивая предпосылка, что движение не существует, является истинной; и действительно, реальность движения — это именно то, что Парменид отрицал.
Получите эксклюзивный доступ к контенту из нашего первого издания 1768 года с вашей подпиской.
Подпишитесь сегодня
,
Центральное место в любой теории множеств имеет формулировка условий
какие наборы сформированы. В дополнение к простому перечислению членов
набора, первоначально предполагалось, что любое четко определенное условие (или
точно указанное свойство) может быть использовано для определения множества. Для
Например, если T является свойством быть чайной чашкой, то
набор S из всех чашек может быть определен как S =
{ x : T ( x )}, набор всех
особи, x , так что x имеет свойство
Т .Даже противоречивое свойство может быть использовано для
определить набор. Например, свойство быть T
и не — T будет определять пустой набор, набор не имеющий
члены.
Точнее, теория наивного множества предполагает так называемое наивное
или неограниченная аксиома понимания, аксиома, которая для любой формулы
φ ( x ), содержащий x в качестве свободной переменной, будет
существует множество { x : φ ( x )}, членами которого являются
именно те объекты, которые удовлетворяют φ ( x ).Таким образом, если
формула φ ( x ) означает « x
простое число », тогда { x : φ ( x )} будет набором
простые числа. Если φ ( x ) означает «~ ( x »)
= x ) », то { x : φ ( x )} будет
пустой набор.
Но из предположения этой аксиомы,
Рассел противоречие следующим образом. Например, если мы
пусть φ ( x ) обозначает x ∈ x и
пусть R = { x : ~ φ ( x )},
тогда R — это множество, членами которого являются именно эти объекты
которые не являются членами самих себя.
Является ли R самим собой? Если это так, то он должен удовлетворять
условие не быть членом самого себя и поэтому это не так. Если это
нет, то он не должен удовлетворять условию не быть членом
сам, и поэтому он должен быть членом самого себя. Так как по классической логике
один случай или другой должны быть выполнены — либо R является членом
само по себе или нет — отсюда следует, что теория подразумевает
противоречие.
Как говорит нам Рассел, это было после того, как он применил такой же вид
рассуждения, найденные в диагональном аргументе Кантора
класс всех мыслимых объектов », что он привел к
противоречие:
Всесторонний класс, который мы рассматриваем, который должен охватить
все, должен принять себя в качестве одного из своих членов.Другими словами,
если есть такая вещь, как «все», то
«Все» является чем-то, и является членом класса
«все.» Но обычно класс не является членом
сам. Человечество, например, не человек. Сформируйте сейчас сборку
все классы, которые не являются членами самих себя. Это класс: есть
это член сам по себе или нет? Если это так, это один из тех классов
которые не являются членами самих себя, то есть не являются членами
сам. Если это не так, это не один из тех классов, которые не являются
члены самих себя, я.е. это член самого себя. Таким образом, из двух
гипотезы — что это, и что это не, член
Сам по себе — каждый подразумевает свое противоречие. Это
противоречие. (1919, 136)
Стандартные ответы на парадокс пытаются каким-то образом ограничить
условия, при которых образуются множества. Целью обычно является
исключить R (и аналогичные противоречивые наборы) и, на
в то же время, чтобы сохранить все другие наборы, необходимые для математики. Это
часто делается путем замены неограниченной аксиомы понимания на более
Аксиома ограничительного разделения, а именно аксиома, которая дана (согласована)
установите S и любую формулу φ ( x ) со свободным x , будет набор
{ x ∈ S : φ ( x )}, членами которого являются
именно те члены S , которые удовлетворяют φ ( x ).Если
мы теперь пусть φ ( x ) означает формулу x
83 x , получается, что соответствующий набор, { x
∈ S : x ∉ x } не будет противоречивым
так как он состоит только из тех членов, найденных в S, которые не являются членами
о себе. Следовательно, набор не может включать себя.
Разнообразие связанных парадоксов обсуждается во второй главе
Вступление к Уайтхеду и Расселу (1910, 2-е изд 60-65), а
ну как в записи на
парадоксы и современная логика
в этой энциклопедии.
Рассел, похоже, обнаружил свой парадокс в конце весны
1901, работая над своими Основы математики
(1903 г.). Точно, когда открытие имело место, не ясно. Рассел
Первоначально говорится, что он столкнулся с парадоксом «в июне
1901 »(1944, 13). Позже он сообщает, что открытие
место «весной 1901 года» (1959, 75). Еще позже он
сообщает, что столкнулся с парадоксом не в июне, а в мае
тот год (1969, 221). Чезаре Бурали-Форти, помощник Джузеппе
Пеано обнаружил подобную антиномию в 1897 году, когда заметил, что
так как множество ординалов хорошо упорядочено, оно тоже должно иметь
порядковый.Тем не менее, этот порядковый номер должен быть одновременно элементом набора
все порядковые и все же больше, чем каждый такой элемент.
В отличие от парадокса Бурали-Форти, парадокс Рассела не связан с
либо ординалы или кардиналы, полагаясь вместо этого только на примитив
Понятия набора и включения набора. Цермело заметил подобное
противоречие где-то между 1897 и 1902, возможно, предвидя
Расселу через несколько лет (Ebbinghaus and Peckhaus 2007, 43–48;
Tappenden 2013, 336), хотя Канамори приходит к выводу, что открытие
могло легко быть уже в 1902 году (Канамори 2009, 411).В любом
В этом случае парадокс считался второстепенным, пока
понял, насколько вредным это было для Готтлоба Фреге
основы математики.
Рассел написал Фреге с новостями о своем парадоксе 16 июня 1902 года.
соответствующую переписку см. Рассел (1902) и Фреге (1902) в
van Heijenoort (1967).) Парадокс имел значение для Фреге
логическая работа, поскольку, по сути, он показал, что аксиомы Фреге
использование для формализации его логики было противоречивым. В частности, Фреге
Аксиома V требует, чтобы выражение, такое как φ ( x ), было
рассматривается как функция аргумента x и функция
аргумента ф.(Точнее, закон Фреге гласит, что
ход ценностей концепции f идентичен
ход значений концепции г тогда и только тогда, когда г
и g согласовывают значение каждого аргумента, то есть, если и только
если для каждого объекта x , f ( x )
= г, ( х ). Смотрите раздел 2.4.1 записи
на Готтлоба Фреге в этой энциклопедии для более
обсуждение.) По сути, именно эта двусмысленность позволила Расселу
построить R таким образом, чтобы он мог быть и не быть
член сам по себе.
Письмо Рассела пришло как раз во втором томе Фреге
Grundgesetze der Arithmetik ( Основные законы
Арифметика , 1893, 1903) была в печати. Сразу оцениваю
трудность, которую поставил парадокс, добавил Фреге к
Grundgesetze наспех составленное приложение, обсуждающее
Открытие Рассела. В приложении Фреге отмечает, что
Последствия парадокса Рассела не сразу ясны. Для
Например: «Всегда ли можно говорить о расширении
концепция, класс? И если нет, то как мы узнаем исключительное
случаи? Можем ли мы всегда сделать вывод из расширения одной концепции
совпадает с секундой, что каждый объект, который попадает под
первая концепция тоже подпадает под вторую? Эти
вопросы, — отмечает Фреге, — поднятые г-ном Расселом
общение »(1903, 127).Из-за этих забот Фреге
в конце концов почувствовал себя вынужденным отказаться от многих своих взглядов на логику и
математика.
Тем не менее, как указывает Рассел, Фреге встретил новость о парадоксе с
замечательная сила духа:
Когда я думаю об актах честности и благодати, я понимаю,
что мне нечего сравнивать с Фреге
преданность истине. Работа всей его жизни была на грани
завершение, большая часть его работы была проигнорирована в пользу мужчин
бесконечно менее способный, его второй том должен был быть опубликован,
и обнаружив, что его основное предположение было ошибочным, он
ответил с интеллектуальным удовольствием, явно погружая любые чувства
личного разочарования.Это было почти сверхчеловечески и показательно
признак того, на что способны люди, если их преданность
творческий труд и знания вместо грубых усилий доминировать и
быть известным. (Цитируется в van Heijenoort (1967), 127)
Конечно, Рассел тоже был обеспокоен последствиями
противоречие. Узнав, что Фреге согласился с ним о
Значение результата он сразу начал писать приложение
за его собственные, которые скоро будут выпущены Основы математики.
Под названием «Приложение B: Учение о типах», приложение
представляет первую попытку Рассела предоставить принципиальный метод
для того, чтобы избежать того, что скоро должно было стать известным как «Рассел
парадокс.»
Значение парадокса Рассела можно увидеть, когда он
понял, что, используя классическую логику, все предложения следуют из
противоречие. Например, если предположить, что P и ~ P,
любое произвольное предложение, Q , может быть доказано следующим образом: из
P получаем P 000 Q по правилу
Сложение; затем из P ∨ Q и ~ P мы
получить Q по правилу дизъюнктивного силлогизма.Потому что установлено
теория лежит в основе всех разделов математики, многие люди начали
беспокоиться о том, что несоответствие теории множеств будет означать, что нет
математическое доказательство может быть полностью заслуживающим доверия. Только
устранение парадокса Рассела может в целом вернуть математике
консистенция.
Парадокс Рассела в конечном счете проистекает из идеи, что любой
условие или свойство могут быть использованы для определения набора. Например,
свойство равномерно делиться только на себя и номер один
отличает множество простых чисел от множества целых
номера.Свойство наличия молочных желез отличает набор
млекопитающих из рептилий, птиц и других живых организмов.
свойство быть как квадратным, так и не квадратным (или любым другим соединением
противоречивых свойств) определяет пустое множество и т. д.
Один ранний скептик относительно неограниченного понимания (или
Абстракция) Аксиома была создателем современной теории множеств, Георг
Кантор. Еще до открытия Рассела Кантор отверг
Неограниченное понимание в пользу того, что было, по сути,
различие между наборами и классами, признавая, что некоторые свойства
(например, свойство быть порядковым) произведенные коллекции, которые
были просто слишком большими, чтобы быть сетами, и что любое предположение к
наоборот приведет к несогласованности.(Подробности можно найти в Мур
(1982), Hallett (1984) и Menzel (1984).)
Собственный ответ Рассела на парадокс пришел с его метким именем
теория типов.
Полагая, что самоприменение лежит в основе парадокса,
Основная идея Рассела заключалась в том, что мы можем избежать приверженности
R (набор всех наборов, которые не являются членами самих себя)
расположение всех предложений (или, точнее, всех
пропозициональные функции,
функции, которые дают предложения в качестве своих значений) в иерархию.Тогда возможно
относятся ко всем объектам, для которых выполняется данное условие (или предикат)
только если они все находятся на одном уровне или одинаково
«тип.»
Это решение парадокса Рассела во многом мотивировано
принятие так называемого принципа порочного круга .
принцип в действительности гласит, что никакая пропозициональная функция не может быть
определяется до указания области применения функции. В
Другими словами, прежде чем функция может быть определена, необходимо сначала указать
именно те объекты, к которым будет применяться функция (функция
домен).Например, перед определением предиката «это простое число
число », сначала нужно определить коллекцию объектов
которые могли бы удовлетворить этот предикат, а именно
набор N натуральных чисел.
Как объясняют Уайтхед и Рассел,
Анализ парадоксов, которых следует избегать, показывает, что все они являются результатом
вид замкнутого круга. Порочные круги, о которых идет речь, возникают из предположения
что коллекция объектов может содержать элементы, которые могут быть определены только
с помощью коллекции в целом.Так, например, коллекция
предложений будет содержать предложение
заявляя, что «все предложения являются либо истинными, либо ложными». Было бы
кажется, однако, что такое заявление не может быть законным, если
«Все предложения» относятся к некоторой уже определенной коллекции, которая
это не может быть сделано, если новые предложения создаются заявлениями о «всем
предложения «. Поэтому мы должны сказать, что заявления о
«Все предложения» не имеют смысла. … Принцип, который
Позволяет нам избежать незаконной совокупности, может быть заявлено следующим образом:
«Что бы ни касалось , все коллекции не должны быть одним из
коллекция»; или, наоборот: «Если, если определенная коллекция имела
итого, он будет иметь членов, определяемых только с точки зрения этой суммы,
то указанная коллекция не имеет итого.Назовем это
«Принцип замкнутого круга», потому что он позволяет нам избежать порочного круга
круги, вовлеченные в предположение о незаконности
тотальности. (1910, 2nd edn 37)
Если Уайтхед и Рассел правы, значит, никакой
Сфера применения когда-либо сможет включать любой объект
предполагает сама функция. В результате, предложения
функции (вместе с соответствующими предложениями) в конечном итоге
быть организованным в иерархии, которую предлагает Рассел.
Хотя Рассел впервые представил свою теорию типов в 1903 году
Основы математики , он сразу признал, что
нужно было проделать больше работы, так как его первоначальный отчет, казалось,
разрешить некоторые, но не все парадоксы. Среди альтернатив он
рассматривалась так называемая теория замещения (Galaugher
2013). Это, в свою очередь, привело к более зрелому выражению теории типов
лет спустя в статье Рассела 1908 года «Математическая логика как
На основе теории типов »и в монументальном труде он
в соавторстве с
Альфред Норт Уайтхед,
Principia Mathematica
(1910, 1912, 1913).Теория типов Рассела, таким образом, появляется в двух
версии: «простая теория» 1903 года и
«Разветвленная теория» 1908 года. Обе версии были
подвергнут критике за то, что он был слишком специальным, чтобы устранить парадокс
успешно.
В ответ на парадокс Рассела,
Дэвид Гильберт также расширил свою программу
построения последовательной, аксиоматической основы математики, чтобы она
включил аксиоматическое обоснование логики и теории множеств (Пекхаус
2004). В основе этого формалистского подхода к была идея
использование только конечных, четко определенных и конструируемых объектов,
вместе с правилами вывода считается абсолютно определенным.
Наконец, Луитцен Брауэр
разработал интуиционизм , основной идеей которого было то, что нельзя
утверждать о существовании математического объекта, если только вы не можете определить
порядок его построения.
Вместе все эти ответы помогли сосредоточить внимание на
связь между логикой, языком и математикой. Они также помогли
логики развивают четкое понимание природы формальных
системы и виды металогико-метаматематических результатов
которые оказались центральными для исследования основ логики
и математика за последние сто лет.
Парадокс Рассела иногда рассматривается как негативное развитие —
как сбить Grundgesetze Фреге и как один из
оригинальные концептуальные грехи, ведущие к нашему изгнанию из Кантора
рай. W.V. Куайн описывает парадокс как
«антиномия», которая «преподносит сюрприз, который может быть
не менее чем отказ от нашего концептуального
наследие »(1966, 11). Куайн имеет в виду наивный
Принцип понимания, упомянутый ранее. В символах принцип
утверждает, что
(NC) ∃ A ∀ x ( x
∈ A ≡ φ),
где A не является свободным в формуле φ.Это говорит,
«Существует набор A такой, что для любого
объект x , x является элементом A , если и только
если условие, выраженное φ, выполнено ». Парадокс рассела
возникает, принимая φ за формулу: x
000 x .
Несмотря на комментарий Куайна, парадокс Рассела можно увидеть в более
позитивный свет. С одной стороны, хотя вопрос остается
Спорные, более поздние исследования показали, что парадокс не
обязательно короткое замыкание Фреге вывод арифметики из логики
в одиночестве.Версия NC Фреге (его Аксиома V) может быть просто
отказались. (Подробнее см. Запись
по теореме Фреге.) Для другого,
Церковь дает элегантную формулировку
простая теория типов, которая оказалась плодотворной даже в областях
снято с основ математики. (Подробнее см.
запись по теории типов.) Наконец,
развитие аксиоматических (в отличие от наивных) множеств теорий, которые
выставлять различные гениальные и математически и философски
значительные способы борьбы с парадоксом Рассела проложили путь к
потрясающие результаты в метаматематике теории множеств.Эти результаты
включили Геделя и Коэна
теоремы о независимости
Аксиома выбора и континуум Кантора
гипотеза. Итак, давайте посмотрим, примерно, как некоторые из этих методов —
в частности, так называемые «нетипизированные» методы — имеют дело с парадоксом Рассела.
Цермело заменяет NC следующей аксиомной схемой разделения
(или Aussonderungsaxiom ):
(ZA) 000 A ∃ B ∀ x
( x ∈ B ≡ ( x ∈ A
∧ φ)).
Опять же, чтобы избежать округлости, B не может быть свободным в φ. это
требует, чтобы для входа в B , x должны
быть членом существующего набора A . Как можно себе представить, это
требует множества дополнительных аксиом существования множества, ни одна из которых
потребовалось бы, если бы NC задержался.
Как Зеир Анпин избегает парадокса Рассела? Сначала можно подумать, что это
не делает. В конце концов, если мы позволим A быть V — все
вселенная множеств — и φ будет x ∉ x , а
опять возникает противоречие.Но в этом случае все
противоречие показывает, что V не является множеством. Все противоречие
показывает, что «V» является пустым именем (то есть, что оно не имеет
ссылка, что V не существует), так как онтология Цермело
Система состоит исключительно из наборов.
Эту же мысль можно сформулировать еще одним способом, включая
релятивизированная форма аргумента Рассела. Пусть B будет любым множеством. По
ZA, набор R B = { x
∈ B : x 000 x } существует, но
не может быть элементом B .Ибо если это элемент
B , то мы можем спросить, является ли это элемент
из R B ; и это если и только если это не так. таким образом
что-то, а именно R B , «отсутствует»
из каждого набора B . Итак, еще раз, V не является множеством, так как ничего не может
отсутствует в V. Но обратите внимание на следующую тонкость: в отличие от
предыдущий аргумент, связанный с прямым применением
Aussonderungs до V, нынешний аргумент намекает на идею
что, хотя V не является множеством, «V» не является пустым именем.
следующая стратегия для решения парадокса Рассела основывается на этом
намекают.
Нетипизированный метод Джона фон Неймана (1925) для решения парадоксов,
и, в частности, парадокс Рассела прост и гениален. фон
Нейман вводит различие между членством и отсутствием членства
и на этой основе проводит различие между наборами и классами.
объект является членом , (упрощенный), если он является членом некоторых
класс; и не является членом , если он не является членом какого-либо
класс.(На самом деле, фон Нейман развивает теорию функций, принятую как
примитивные, а не классы, в которых соответствующие
различие между членом и не членом состоит в различении объекта
это может быть аргументом какой-то функции, а другой — нет. В своем
современная форма, благодаря Бернайсу и Гёделю,
это односортная теория классов.)
Затем наборы определяются как члены, а не-члены помечаются
«Правильные занятия». Так, например, Рассел
класс, R , не может быть членом какого-либо класса, и, следовательно, он должен
быть правильным классом.Если R предполагается как элемент класса
А , то это следует из одной из аксиом фон Неймана
что R не эквивалентно V . Но R это
эквивалентно V , и, следовательно, не является элементом A . Таким образом,
Метод фон Неймана тесно связан с результатом, изложенным выше
о наборе R B , для произвольной B . фон
Метод Неймана, хотя восхищаются такими, как Гедель и
Bernays, был недооценен в последние годы.
Куайн (1937) и (1967) аналогичным образом предлагают другой нетипизированный метод (в
письмо, если не в духе) блокирования парадокса Рассела, и тот, который
изобилует интересными аномалиями. Основная идея Куайна состоит в том, чтобы представить
стратифицированная аксиома понимания . По сути, блоки аксиомы
округлость путем введения иерархии (или стратификации), которая
похож на теорию типов в некоторых отношениях, и отличается в других. (Подробности
можно найти в записи на
Новые фонды Куайна.)
В отличие от стратегий Цермело, фон Неймана и Куайна, которые
в некотором смысле чисто теоретический набор, были также попытки
избежать парадокса Рассела, изменив основную логику.Там есть
было много таких попыток и мы не будем их пересматривать, но одну
в настоящее время выделяется как радикальный и несколько популярный
(хотя не с установленными теоретиками как таковыми ): это
паранепротиворечивый подход , который ограничивает общий эффект
изолированного противоречия на всей теории. Классическая логика
мандаты, что любое противоречие упрощает теорию, делая каждый
Предложение теории доказуемо. Это потому, что в классической логике
следующая теорема:
( Ex Falso Quadlibet ) A ⊃ (~ A ⊃ B).
Теперь практически единственный способ избежать EFQ — отказаться от дизъюнктивного
силлогизм, то есть, учитывая обычные определения
соединительные, modus ponens ! Так что изменение базовой логики предложений
таким образом, это действительно радикально — но возможно. К сожалению,
даже отказа от EFQ недостаточно для сохранения подобия NC. Один
также должен отказаться от следующей дополнительной теоремы
логика предложения:
(Сокращение) (A ⊃ (A ⊃ B)) ⊃ (A ⊃ B).
Затем можно утверждать, что НК ведет непосредственно, а не просто к
изолированное противоречие, но до мелочности.(Для аргумента, что это
это так, смотрите запись на
Парадокс карри,
раздел 2.2. Заметьте также, что недостаточно просто
сохранить название « modus ponens »; это правило
сам, который изменяется в нетрадиционной логике.)
Кажется, что беды NC не ограничиваются парадоксом Рассела, но
также включают парадокс без отрицаний из-за Карри.
Другое предложение может заключаться в том, что парадокс зависит
на примере принципа исключенного среднего, что
либо R является членом R , либо нет.Это
принцип, который отвергается некоторыми неклассическими подходами к логике,
в том числе интуиционизм. Однако можно сформулировать
парадокс, не обращаясь к Исключенному Среднему, полагаясь вместо этого на
Закон непротиворечия. Мы делаем это следующим образом: учитывая
Из определения R следует, что R ∈ R
≡ ~ ( R ∈ R ). Итак, R
∈ R ⊃ ~ ( R ∈ R ). Но мы также
известно, что R ∈ R ⊃ R
∈ R .Итак, R ∈ R ⊃ ( R
∈ R ∧ ~ ( R ∈ R )). Но по
Закон непротиворечивости мы знаем, что ~ ( R ∈ R
∧ ~ ( R ∈ R )). Итак, модус толленс
мы заключаем, что ~ ( R ∈ R ). В то же время мы
Также известно, что с R ∈ R ≡ ~ ( R
∈ R ), то ~ ( R ∈ R )
000 R ∈ R и, таким образом, что R
∈ R .Таким образом, мы можем вывести как R ∈ R
и его отрицание с использованием только интуитивно приемлемых методов.
Следовательно, кажется, что сторонники неклассической логики не могут
утверждают, что сохранили NC в каком-либо значительном смысле, кроме
сохраняя чисто синтаксическую форму принципа, и ни
Интуиционизм или параконсистенция плюс отказ от Сокращения
предложит преимущество перед нетипизированными решениями Zermelo, von
Нейман или Куайн. (Дальнейшее обсуждение можно найти в Meyer, Routley
и Dunn (1979), Irvine (1992), Priest (2006, ch.18), Weber (2010),
Вебер (2012) и в записях на
Парадокс карри (с. 2.2)
и
паранепротиворечивая логика (п. 2.3).)
Стоит также отметить, что парадокс Рассела был не единственным
парадокс, который беспокоил Рассела и, следовательно, не единственная мотивация
ограничения типа, которые можно найти в Principia Mathematica. В
его ранняя работа, Принципы математики , Рассел
посвящает главу «Противоречие» (Рассел
парадокс), представляя его в нескольких формах и отклоняя несколько
не стартовые ответы.Затем он сигнализирует, что он будет
«Вкратце» обсудим учение о типах. Это не
произойдет на несколько сотен страниц, пока мы не достигнем самого конца
книга, в приложении B! Там Рассел дарит начинающему, простому
теория типов, а не теория типов, которую мы находим в Принципы
Mathematica. Зачем нужна была более поздняя теория? Причина в том, что
в Приложении B Рассел также представляет еще один парадокс, который он считает
не может быть решена с помощью простой теории типов. Это новый
Парадокс касается предложений, а не классов, и это, вместе с
семантические парадоксы, побудившие Рассела сформулировать свою разветвленную версию
теория типов.
Новая, пропозициональная версия парадокса не выяснила
заметно в последующем развитии логики и теории множеств, но
это очень озадачило Рассела. Во-первых, это кажется противоречащим
Теорема Кантора. Рассел пишет: «Мы не можем допустить, чтобы
больше диапазонов [классов предложений], чем предложений »
(1903, 527). Причина в том, что там, кажется, легко, один на один
корреляции между классами суждений и суждений. Для
Например, класс предложений м можно соотнести с
утверждение, что каждое предложение в м верно.Это,
вместе с детальным принципом индивидуации для
предложения (утверждая, с одной стороны, что, если классы м
и n предложений отличаются, то любое предложение
около м будет отличаться от любого предложения около н )
приводит к противоречию.
Там было относительно мало дискуссий об этом парадоксе, хотя
это сыграло ключевую роль в развитии церковной логики смысла и
денотат. Хотя у нас есть несколько наборов теорий на выбор, мы делаем
не имеет ничего общего с развитой теорией Расселла
предложения, хотя такие предложения имеют решающее значение для
Миллианцы и теоретики прямых ссылок.Казалось бы, что такое
теория была бы необходима для основ семантики, если бы не
основы математики. Таким образом, пока один из парадоксов Рассела
привело к плодотворному развитию основ математики,
его «другой» парадокс еще ни к чему не привел
похоже на основы семантики. Безусловно, Церковь (1974a)
и Андерсон (1989) попытались разработать интенсивные расселлы
логика основана на разветвленной теории типов, но аргумент может быть
сделал, что разветвленная теория слишком ограничительна, чтобы служить
основа семантики естественного языка.Там также есть
были некоторые недавние попытки получить начало Расселласа
интенциональная логика, основанная на нетипизированных теориях множеств (Cantini 2004;
Дойч 2014). Довольно иронично, что, хотя мелкозернистый
Расселевские суждения одобряются в философии языка,
формальное развитие интенциональной логики доминирует Монтегю
грамматика с ее конечно-детальной теорией высказываний.
Стоит также отметить, что ряд, казалось бы, чисто
Теоретико-множественные принципы являются фактически (прикладными) примерами
теоремы чистой логики (т.е.теории квантования первого порядка
с личностью)! Есть (частичный) список из них на калишском,
Монтегю и Мар (2000). Парадокс Рассела является примером T269 в
этот список:
(T269) ~ y ∀ x ( Fxy ≡
~ Fxx ).
Чтение двоичного предиката « F » как
«Является членом», это говорит о том, что это не тот случай, когда
существует y , такой что для любого x , x является
участник y тогда и только тогда, когда x не является членом
х .Означает ли это, что парадокс Рассела сводится к
T269?
Конечно, доказательство T269 рассеивает суть Рассела
аргумент, его модель рассуждения. Но эта модель также гарантирует
бесконечный список на первый взгляд несерьезных «парадоксов», таких как
знаменитый парадокс парикмахера, который бреет всех и только тех, кто делает
не брить себя или, аналогично, парадокс доброжелательного, но
действенный Бог, который помогает всем и только тем, кто не помогает
самих себя.
Как эти «псевдо парадоксы», как они иногда
называется, чем отличается от парадокса Рассела? Образец
рассуждения такие же и вывод — что такого нет
Парикмахер, нет такого эффективного Бога, нет такого набора несамостоятельных наборов
— то же самое: таких вещей просто не существует.(Однако, как фон
Нейман показал, что нет необходимости заходить так далеко. фон
Метод Неймана не учит нас, что такие вещи, как R делают
не существует, но только то, что мы не можем сказать о них много, поскольку
как R и тому подобное, не может входить в расширение любого
предикат, который квалифицируется как класс.)
Стандартный ответ на этот вопрос заключается в том, что разница заключается в
предмет. Куайн спрашивает: «Почему это [Рассел
парадокс] считается антиномией, а парадокс парикмахера нет? »; и
он отвечает: «Причина в том, что в наших привычках
думал подавляющее предположение о существовании такого класса, но нет
презумпция существования такого парикмахера »(1966, 14).Несмотря на это,
психологический разговор о «привычках мышления» не
особенно осветительно Более того, парадокс Рассела
разумно порождает вопрос о том, какие существуют множества; но это
бессмыслица удивляться, на таких основаниях, как T269, какие парикмахеры или боги
есть!
Однако этот вердикт не совсем справедлив по отношению к поклонникам парикмахера или
Т269 в общем. Они будут настаивать на том, что вопрос, поднятый T269,
не то, что есть парикмахеры или боги, а то, что не парадоксально
объекты есть.Этот вопрос практически такой же, как поднятый
по самому парадоксу Рассела. Таким образом, с этой точки зрения
связь между парадоксом Парикмахера и Рассела намного ближе, чем
многие (после Куайна) были готовы разрешить (Salmon 2013).
Отметим, что существует логическая формула первого порядка, которая имеет
То же отношение к принципу R B
T269 несет в себе парадокс Рассела. Это следующее:
(T273) 000 z ∀ y (000 x
[ Fxy ≡ ( Fxz ∧ ~ Fxx )] ⊃
~ Физ ).
(Мы позволили себе расширить нумерацию, используемую в
Калиш, Монтегю и Мар (2000) до T273.) Но не все теоретико-множественные
Парадоксы аналогично связаны с логическими теоремами первого порядка.
Парадокс Бурали-Форти является примером, так как понятие
упорядоченность не элементарна; то есть это не первый порядок
определимы.
Парадокс Рассела никогда не был пассивным, но в последнее время
был взрыв интереса к нему учеными, вовлеченными в исследование
в математической логике и в философско-исторических исследованиях
современная логика.Взгляд на содержание тома 2004 года Один
Парадокс Рассела «Сто лет» показывает выдающиеся математические
и философские логики и историки логики льются над
парадокс, предлагая новые пути назад в рай Кантора, или другие пути
решения вопроса. Их исследования включают в себя радикально новые
Выход из дилеммы, порожденной парадоксом, новые исследования
теории типов (простые и разветвленные и их расширения), новые
интерпретации парадокса и конструктивных теорий Рассела,
парадокса расселов суждений и его собственной попытки нетипизированного
теория (теория замещения) и пр.
Все это напоминает нам
что плодотворная работа может возникнуть в результате
наблюдения. Как сказала Дана Скотт: «Это нужно понимать
с самого начала, что парадокс Рассела — это , а не
как катастрофа. Это и связанные с этим парадоксы показывают, что наивный
Понятие все включено коллекции несостоятельно. Это
Интересный результат, в этом нет сомнений »(1974, 207).
,









































