Теория пара: Насыщенный пар — материалы для подготовки к ЕГЭ по Физике

Насыщенный пар — материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: насыщенные и ненасыщенные пары, влажность воздуха.

Если открытый стакан с водой оставить на долгое время, то в конце концов вода полностью улетучится. Точнее — испарится. Что такое испарение и почему оно происходит?

Испарение и конденсация

При данной температуре молекулы жидкости обладают разными скоростями. Скорости большинства молекул находятся вблизи некоторого среднего значения (характерного для этой температуры). Но попадаются молекулы, скорости которых значительно отличаются от средней как в меньшую, так и большую сторону.

На рис. 1 изображён примерный график распределения молекул жидкости по скоростям. Голубым фоном показано то самое большинство молекул, скорости которых группируются около среднего значения. Красный «хвост» графика — это небольшое число «быстрых» молекул, скорости которых существенно превышают среднюю скорость основной массы молекул жидкости.

Рис. 1. Распределение молекул по скоростям

Когда такая весьма быстрая молекула окажется на свободной поверхности жидкости (т.е. на границе раздела жидкости и воздуха), кинетической энергии этой молекулы может хватить на то, чтобы преодолеть силы притяжения остальных молекул и вылететь из жидкости. Данный процесс и есть испарение, а молекулы, покинувшие жидкость, образуют пар.

Итак, испарение — это процесс превращения жидкости в пар, происходящий на свободной поверхности жидкости (при особых условиях превращение жидкости в пар может происходить по всему объёму жидкости. Данный процесс вам хорошо известен — это кипение).

Может случиться, что через некоторое время молекула пара вернётся обратно в жидкость.

Процесс перехода молекул пара в жидкость называется конденсацией. Конденсация пара — процесс, обратный испарению жидкости.

Динамическое равновесие

А что будет, если сосуд с жидкостью герметично закрыть? Плотность пара над поверхностью жидкости начнёт увеличиваться; частицы пара будут всё сильнее мешать другим молекулам жидкости вылетать наружу, и скорость испарения станет уменьшаться. Одновременно начнёт увеличиваться скорость конденсации, так как с возрастанием концентрации пара число молекул, возвращающихся в жидкость, будет становиться всё больше.

Наконец, в какой-то момент скорость конденсации окажется равна скорости испарения. Наступит динамическое равновесие между жидкостью и паром: за единицу времени из жидкости будет вылетать столько же молекул, сколько возвращается в неё из пара. Начиная с этого момента количество жидкости перестанет убывать, а количество пара — увеличиваться; пар достигнет «насыщения».

Насыщенный пар — это пар, который находится в состоянии динамического равновесия со своей жидкостью. Пар, не достигший состояния динамического равновесия с жидкостью, называется ненасыщенным.

Давление и плотность насыщенного пара обозначаются и . Очевидно, и — это максимальные давление и плотность, которые может иметь пар при данной температуре. Иными словами, давление и плотность насыщенного пара всегда превышают давление и плотность ненасыщенного пара.

Свойства насыщенного пара

Оказывается, что состояние насыщенного пара (а ненасыщенного — тем более) можно приближённо описывать уравнением состояния идеального газа (уравнением Менделеева — Клапейрона). В частности, имеем приближённое соотношение между давлением насыщенного пара и его плотностью:

(1)

Это весьма удивительный факт, подтверждаемый экспериментом. Ведь по своим свойствам насыщенный пар существенно отличается от идеального газа. Перечислим важнейшие из этих отличий.

1. При неизменной температуре плотность насыщенного пара не зависит от его объёма.

Если, например, насыщенный пар изотермически сжимать, то его плотность в первый момент возрастёт, скорость конденсации превысит скорость испарения, и часть пара конденсируется в жидкость — до тех пор, пока вновь не наступит динамическое равновесие, в котором плотность пара вернётся к своему прежнему значению.

Аналогично, при изотермическом расширении насыщенного пара его плотность в первый момент уменьшится (пар станет ненасыщенным), скорость испарения превысит скорость конденсации, и жидкость будет дополнительно испаряться до тех пор, пока опять не установится динамическое равновесие — т.е. пока пар снова не станет насыщенным с прежним значением плотности.

2. Давление насыщенного пара не зависит от его объёма.

Это следует из того, что плотность насыщенного пара не зависит от объёма, а давление однозначно связано с плотностью уравнением (1).

Как видим, закон Бойля — Мариотта, справедливый для идеальных газов, для насыщенного пара не выполняется. Это и не удивительно — ведь он получен из уравнения Менделеева — Клапейрона в предположении, что масса газа остаётся постоянной.

3. При неизменном объёме плотность насыщенного пара растёт с повышением температуры и уменьшается с понижением температуры.

Действительно, при увеличении температуры возрастает скорость испарения жидкости.

Динамическое равновесие в первый момент нарушается, и происходит дополнительное испарение некоторой части жидкости. Пара будет прибавляться до тех пор, пока динамическое равновесие вновь не восстановится.

Точно так же при понижении температуры скорость испарения жидкости становится меньше, и часть пара конденсируется до тех пор, пока не восстановится динамическое равновесие — но уже с меньшим количеством пара.

Таким образом, при изохорном нагревании или охлаждении насыщенного пара его масса меняется, поэтому закон Шарля в данном случае не работает. Зависимость давления насыщенного пара от температуры уже не будет линейной функцией.

4. Давление насыщенного пара растёт с температурой быстрее, чем по линейному закону.

В самом деле, с увеличением температуры возрастает плотность насыщенного пара, а согласно уравнению (1) давление пропорционально произведению плотности на температуру.

Зависимость давления насыщенного пара от температуры является экспоненциальной (рис. 2). Она представлена участком 1–2 графика. Эту зависимость нельзя вывести из законов идеального газа.

Рис. 2. Зависимость давления пара от температуры

В точке 2 вся жидкость испаряется; при дальнейшем повышении температуры пар становится ненасыщенным, и его давление растёт линейно по закону Шарля (участок 2–3).

Вспомним, что линейный рост давления идеального газа вызван увеличением интенсивности ударов молекул о стенки сосуда. В случае нагревания насыщенного пара молекулы начинают бить не только сильнее, но и чаще — ведь пара становится больше. Одновременным действием этих двух факторов и вызван экспоненциальный рост давления насыщенного пара.

Влажность воздуха

Воздух, содержащий водяной пар, называется влажным.Чем больше пара находится в воздухе, тем выше влажность воздуха.

Абсолютная влажность — это парциальное давление водяного пара, находящегося в воздухе (т. е. давление, которое водяной пар оказывал бы сам по себе, в отсутствие других газов). Иногда абсолютной влажностью называют также плотность водяного пара в воздухе.

Относительная влажность воздуха — это отношение парциального давления водяного пара в нём к давлению насыщенного водяного пара при той же температуре. Как правило, это отношение выражают в процентах:

Из уравнения Менделеева-Клапейрона (1) следует, что отношение давлений пара равно отношению плотностей. Так как само уравнение (1), напомним, описывает насыщенный пар лишь приближённо, мы имеем приближённое соотношение:

Одним из приборов, измеряющих влажность воздуха, является психрометр. Он включает в себя два термометра, резервуар одного из которых завёрнут в мокрую ткань. Чем ниже влажность, тем интенсивнее идёт испарение воды из ткани, тем сильнее охлаждается резервуар «мокрого» термометра, и тем больше разность его показаний и показаний сухого термометра. По этой разности с помощью специальной психрометрической таблицы определяют влажность воздуха.

Теория пары. — Студопедия

На рис. 17 изображена схема обобщенной термодинамической пары, в которой места спаев обладают емкостями (резервуарами) второго экстенсора К₂^’ и К₂. В общем случае между каждой емкостью и проводниками а и б имеются свои скачки второго интенсиала. Суммарные скачки в первом и втором спаях

dР₂’ = dР_2а’ + dР_2б’ = Р_2а’ — Р_2с’ + Р_2с’ — Р_2б’ = Р_2а’ — Р_2б’; (462)

dР₂” = dР_2а” + dР_2б” = Р_2с” — Р_2а” + Р_2б” — Р_2с” = Р_2б” — Р_2а”; (463)

Фиктивная движущая сила определяется разностью

DР_2с = Р_2с” – Р_2с’. (464)

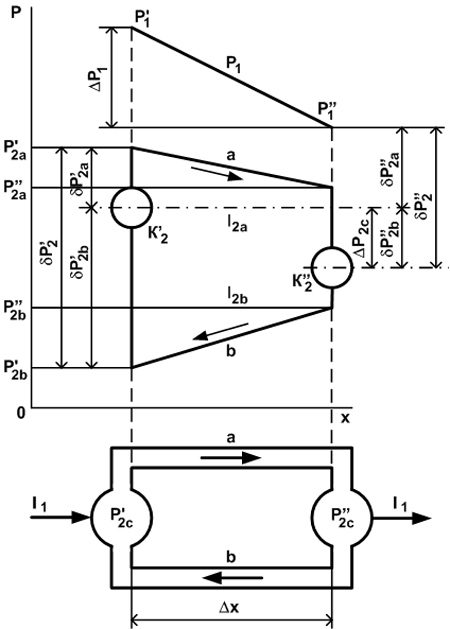Рис. 17. Схема действия обобщенной термодинамической пары.

Обобщенная пара охватывает все основные случаи, встречающиеся на практике. В частности, она описывает фильтрационную пару (рис. 16). Если емкости К₂^’ и К₂” равны нулю, то получается пара, изображенная на рис. 15.

Рассмотрим теперь количественные соотношения, характеризующие работу обобщенной термодинамической пары. Энергию, необходимую для поддержания циркуляции второго экстенсора, поставляют среда и частично движущийся первый экстенсор. В обычных условиях главную долю энергии дают эффекты контактной и линейной диссипации (экранирования). В излагаемой ниже теории для простоты принимается, что в спаях имеются скачки только второго интенсиала. Кроме того, не учитываются некоторые эффекты второго порядка и т.д.

Суммарные контактные в спаях и линейные в проводниках работы второго экстенсора определяются выражениями [14]

dQ_2k = dQ_2д” — dQ_2д’ = dР₂”dE₂ — dР₂’dE₂ = dР_2kdE₂ дж; (465)

dQ_21л = dQ_21б — dQ_21а = dР_21бdE₂ — dР_21аdE₂ = dР_2лdE₂ дж; (466)

где

dР_2k = dР₂” — dР₂’; (467)

dР_2л = dР_21б — dР_21а. (468)

Следовательно, полезная работа циркуляции второго экстенсора

dQ₂ = dQ_2k + dQ_2л = (dР_2k + dР_2л)dE₂ = dР₂dE₂ дж, (469)

где полная движущая сила термодинамической пары

dР₂ = dР_2k + dР_2л. (470)

Контактная составляющая движущей силы dР_2k может быть выражена через разность DР₁ первого интенсиала с помощью уравнения состояния. Например, при dE₂ = 0 из уравнения (26) находим

dР₂ = (А₂₁/А₁₁) dР₁. (471)

Для тел а и б суммарная контактная движущая сила

dР_2k = dР₂” — dР₂’ = Ф₂₁DР₁, (472)

где

Ф₂₁ = (А_21б/А_11б) – (А_21а/А_11а). (473)

У идеальных тел коэффициенты А постоянны, поэтому интенсиалы Р_2а и Р_2б пропорциональны интенсиалу Р₁ и коэффициент

Ф₂₁ = d(dР_2k)/dР₁ = dР_2k/DР₁ = dР₂’/Р₁’ = dР₂”/ Р₁”. (474)

Линейная составляющая движущей силы пары dР_2л определяется несколько сложнее, чем контактная. Из всех эффектов, влияющих на dР_2л, учтем только два. Они связаны с линейным экранированием термиора ансором-носителем, который циркулирует по замкнутой цепи пары. Носитель имеет в своем составе экстенсоры Е₁ и Е₂. При его циркуляции вместе с экстенсором dE₂ преодолевает разность интенсиалов DР₁ также экстенсор dE₁. Первая работа экранирования равна произведению этих величин. Но dE₁ пропорционально dE₂, поэтому работа экранирования пропорциональна DР₁dE₂. Эта работа в соответствии с уравнением состояния изменяет все интенсиалы носителя, включая Р₂. В результате появляется дополнительная движущая сила dР_2л, преодоление которой экстенсором dE₂ сопровождается эффектом экранирования. Учитывая, что dР_2л пропорционально dE₂, окончательно найдем [16]

dQ_21л = (В_21б^’ – В_21а’)DР₁(dE₂)³ = dР_2лdE₂,

где В – коэффициент пропорциональности.

Удобнее всего оперировать секундными работами, т.е. потоками, тогда

I_Qл = (В_21б – В_21а)DР₁I₂³ = dР_2лI₂ вт (475)

и

dР_2л = (В_21б – В_21а)DР₁I₂². (476)

Линейная составляющая движущей силы пропорциональна разности интенсиалов DР₁ и квадрату потока второго экстенсора.

Следовательно, полная движущая сила термодинамической пары

DР₂/DР₁ = (dР_2к/DР₁) + (dР_2л/DР₁) = Ф₂₁ + (В_21б – В_21а)I₂². (477)

Полная движущая сила расходуется на преодоление сопротивлений цепи. Если пренебречь сопротивлениями спаев, тогда связь между движущей силой dР₂, перепадами интенсиала в проводниках а и б

DР_2а = Р_2а^” — Р_2а’; DР_2б = Р_2б^” — Р_2б’ (478)

и сопротивлениями проводников R_2a и R_2б — формула (139) – найдется с помощью выражений

DР_2а = I_2аR_2a + dР_2а; DР_2б = I_2бR_2б + dР_2б. (479)

На стационарном режиме работы пары, когда I_2а = I_2б = I₂, получаем

dР₂ = I₂(R_2a + R_2б) = DР_2а + DР_2б + dР_2л (480)

или

dР_2к = DР_2а + DР_2б. (481)

Сумма измеренных перепадов второго интенсиала вдоль проводников равна контактной составляющей движущей силы.

Под действием движущей силы dР₂ в паре происходит циркуляция второго экстенсора и появляется фиктивная движущая сила DР_2с. Для ее определения представим полную движущую силу в виде

dР₂ = dР_2а + dР_2б, (482)

где dР_2аиdР_2б — движущие силы верхнего и нижнего участков пары (над и под емкостями, рис. 17),

dР_2а = — dР_2а^’ — dР_21а + dР_2а”; dР_2б = — dР_2б^’ + dР_21б + dР_2б”. (483)

Через эти движущие силы путем несложных преобразований можно найти зависимость величины DР_2с от времени. Имеем [10, 11, 14]

DР_2с = (dР_2б – n₂dР_2а)/(1 + n₂){1 – exp[-(1/R_2a + 1/R_2б)(1/К₂’ + 1/К₂”)t]}, (484)

где

n₂ = R_2б/R_2а. (485)

Из этой формула видно, что в начальный момент (t = 0) фиктивная движущая сила равна нулю. С течением времени DР_2с растет по экспоненциальному закону. При t = ¥ наступает стационарный режим, величина DР_2с приобретает максимальное значение

DР_2с = (dР_2б – n₂dР_2а)/(1 + n₂) (486)

В условиях стационарного режима потоки второго экстенсора в проводниках а и б одинаковы. Находим

I_2а¥ = I_2б¥ = (dР_2а + DР_2с¥)/R_2а = (dР_2б — DР_2с¥)/R_2б =

+ (dР_2а + dР_2б)/(R_2а + R_2б) = dР₂/(R_2а + R_2б) (487)

Необходимо подчеркнуть, что величина DР_2с не есть движущая сила процесса циркуляции второго экстенсора, как иногда думают. Фактической движущей силой служит разность dР₂. Исходной причиной функционирования пары являются связи, заключенные в уравнениях состояния. Любая термодинамическая пара представляет собой преобразователь, в котором под действием экранированного термиора происходят взаимные превращения активностей различных элат.

Теория пар сил. Теоремы о парах

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Пара сил — совокупность двух параллельных друг другу сил равных по величине и направленных в противоположные стороны. Пара сил не может быть более упрощена (заменена одной силой) и представляет собой новую силовую характеристику механического взаимодействия.

Теорема о моменте пары сил. Момент пары сил не зависит от выбора центра привидения и равен произведению любой из сил пары на плечо пары, взятый со знаком «+» при вращении пары против часовой стрелки или со знаком «-» при вращении по часовой.

Плечо пары сил — длина перпендикуляра опущенного из любой точки линии действия одной силы к линии действия другой силы этой пары.

Теорема об эквивалентности пар сил в плоскости. Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты численно равны и одинаковы по знаку.

Следствие. Пару сил, не изменяя ее действие на твердое тело, можно переносить в любое место в плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять это плече и модули сил, не изменяя величины ее момента и направления вращения. Следовательно, основной характеристикой пары сил является ее момент.

Теорема об эквивалентности пар сил в пространстве. Пары сил в пространстве эквивалентны, если их моменты геометрически равны.

Следствие. Не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости ее действия, а также изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента. Вектор момента пары сил можно переносить в любую точку, т.е. момент пары сил является свободным вектором. Вектор момента пары сил определяет все три ее элемента: положение плоскости действия пары, направление вращения и числовое значение момента.

Теорема о сложении пар сил на плоскости. Систему пар сил можно заменить парой сил, момент которой равен алгебраической сумме моментов исходных пар. Кинематическое состояние тела не изменяется.

Условие равновесия системы пар сил:

.

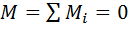18. Статические инварианты и динамические винты

Инварианты системы сил — величины, не зависящие от выбора центра приведения. Первый векторный инвариант — главный вектор системы сил .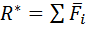

Главный момент не является инвариантом т.к. зависит от центра привидения. Однако существует величина, связанная с главным вектором и не зависящая от центра приведения. Однако существует величина, связанная с главным вектором и не зависящая от центра привидения:

1)

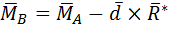
2)

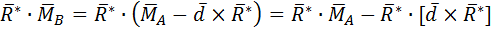
3) .

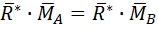Второй скалярный инвариант — скалярное произведение главного вектора на вектор главного момента.

.

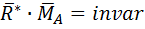Главный минимальный момент также инвариантная величина:

.

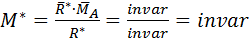Динамический винт — совокупность действующих на тело силы F и пары сил с моментом М, лежащей в плоскости перпендикулярной силе F. К динамическому винту приводится в наиболее общем случае произвольная система сил, действующих на тело. Дальнейшее упрощение динамического винта не возможно, т.е. его нельзя заменить одной силой и одной парой сил. Можно лишь сложив F с одной из сил пары привести его к двум скрещивающимся силам.

Центры тяжести простейших фигур

Фермы. Методы расчета ферм

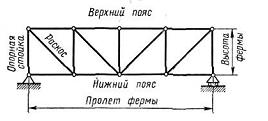Фермой называется геометрически не изменяемая шарнирно-стрежневая конструкция. Если все оси фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс фермы, а расположенные по нижнему контуру — нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные — раскосами.

Способ вырезания узлов. Суть способа заключается в том, что мысленно вырезают каждый узел фермы, прикладывают к нему известные силы и реакции стержней, которые направляют от узла, т.к. неизвестно какие стержни фермы растянуты, а какие сжаты, изначально полагают, что все стержни растянуты, а затем составляются уравнения равновесия сил, приложенных к каждому узлу. Расчет фермы начинают с узлов, к которым приложено не более двух неизвестных сил для плоской фермы, и не более трех для пространственной.

Метод Риттера. Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая их растянутыми. Затем составляют уравнения моментов относительно точек Риттера (точка пересечения двух из трех перерезанных стержней). Из полученных уравнений определяются усилия в стержнях.



Теория пар

Новости

«Викимедиа РУ» провела мастер-класс по работе с «Википедией»
23 июля состоялся вебинар «Секреты Википедии», на котором участники узнали как возникла и функционирует крупнейшая энциклопедия современности, можно ли ей доверять и использовать в учебном процессе, что такое свободные лицензии, каково будущее «Википедии», а также увидели, как писать и редактировать статьи.

Мнения

Виталий Куренной

Традиционные ценности и диалектика критики в обществе сингулярности

Статья Николая Патрушева по поводу российских ценностей интересна сама по себе, но также вызвала яркий отклик Григория Юдина, который разоблачает парадигму «ценностей», трактуя ее, видимо, как нечто сугубо российско-самобытное, а само понятие «ценность» характеризует как «протухшее». Попробую выразить тут свое отношение к этой интересной реплике, а заодно и прокомментировать характер того высказывания, по поводу которого она появилась.

Иван Засурский

Пора начать публиковать все дипломы и диссертации!

Открытое письмо президента Ассоциации интернет-издателей, члена Совета при Президенте Российской Федерации по развитию гражданского общества и правам человека Ивана Ивановича Засурского министру науки и высшего образования Российской Федерации Валерию Николаевичу Фалькову.

Сергей Васильев, facebook.com

Каких денег нам не хватает?

Нужны ли сейчас инвестиции в малый бизнес и что действительно требует вложений

За последние десятилетия наш рынок насытился множеством современных площадей для торговли, развлечений и сферы услуг. Если посмотреть наши цифры насыщенности торговых площадей для продуктового, одёжного, мебельного, строительного ритейла, то мы увидим, что давно уже обогнали ведущие страны мира. Причём среди наших городов по этому показателю лидирует совсем не Москва, как могло бы показаться, а Самара, Екатеринбург, Казань. Москва лишь на 3-4-ом месте.

Иван Засурский

Пост-Трамп, или Калифорния в эпоху ранней Ноосферы

Длинная и запутанная история одной поездки со слов путешественника

Сидя в моём кабинете на журфаке, Лоуренс Лессиг долго и с интересом слушал рассказ про попытки реформы авторского права — от красивой попытки Дмитрия Медведева зайти через G20, погубленной кризисом Еврозоны из-за Греции, до уже не такой красивой второй попытки Медведева зайти через G7 (даже говорить отказались). Теперь, убеждал я его, мы точно сможем — через БРИКС — главное сделать правильные предложения! Лоуренс, как ни странно, согласился. «Приезжай на Grand Re-Opening of Public Domain, — сказал он, — там все будут, вот и обсудим».

Николай Подосокорский

Виртуальная дружба

Тенденции коммуникации в Facebook

Дружба в фейсбуке – вещь относительная. Вчера человек тебе писал, что восторгается тобой и твоей «сетевой деятельностью» (не спрашивайте меня, что это такое), а сегодня пишет, что ты ватник, мерзавец, «расчехлился» и вообще «с тобой все ясно» (стоит тебе написать то, что ты реально думаешь про Крым, Украину, США или Запад).

Марат Гельман

Пособие по материализму

«О чем я думаю? Пытаюсь взрастить в себе материалиста. Но не получается»

Сегодня на пляж высыпало много людей. С точки зрения материалиста-исследователя, это было какое-то количество двуногих тел, предположим, тридцать мужчин и тридцать женщин. Высоких было больше, чем низких. Худых — больше, чем толстых. Блондинок мало. Половина — после пятидесяти, по восьмой части стариков и детей. Четверть — молодежь. Пытливый ученый, быть может, мог бы узнать объем мозга каждого из нас, цвет глаз, взял бы сорок анализов крови и как-то разделил бы всех по каким-то признакам. И даже сделал бы каждому за тысячу баксов генетический анализ.

Дмитрий Волошин, facebook.com/DAVoloshin

Теория самоневерия

О том, почему мы боимся реальных действий

Мы живем в интересное время. Время открытых дискуссий, быстрых перемещений и медленных действий. Кажется, что все есть для принятия решений. Информация, много структурированной информации, масса, и средства ее анализа. Среда, открытая полемичная среда, наработанный навык высказывать свое мнение. Люди, много толковых людей, честных и деятельных, мечтающих изменить хоть что-то, мыслящих категориями целей, уходящих за пределы жизни.

facebook.com/ivan.usachev

Немая любовь

«Мы познакомились после концерта. Я закончил работу поздно, за полночь, оборудование собирал, вышел, смотрю, сидит на улице, одинокая такая. Я её узнал — видел на сцене. Я к ней подошёл, начал разговаривать, а она мне «ыыы». Потом блокнот достала, написала своё имя, и добавила, что ехать ей некуда, с парнем поссорилась, а родители в другом городе. Ну, я её и пригласил к себе. На тот момент жена уже съехала. Так и живём вместе полгода».

Михаил Эпштейн

Симпсихоз. Душа — госпожа и рабыня

Природе известно такое явление, как симбиоз — совместное существование организмов разных видов, их биологическая взаимозависимость. Это явление во многом остается загадкой для науки, хотя было обнаружено швейцарским ученым С. Швенденером еще в 1877 г. при изучении лишайников, которые, как выяснилось, представляют собой комплексные организмы, состоящие из водоросли и гриба. Такая же сила нерасторжимости может действовать и между людьми — на психическом, а не биологическом уровне.

Лев Симкин

Человек из наградного листа

На сайте «Подвиг народа» висят наградные листы на Симкина Семена Исааковича. Моего отца. Он сам их не так давно увидел впервые. Все четыре. Последний, 1985 года, не в счет, тогда Черненко наградил всех ветеранов орденами Отечественной войны. А остальные, те, что датированы сорок третьим, сорок четвертым и сорок пятым годами, выслушал с большим интересом. Выслушал, потому что самому читать ему трудновато, шрифт мелковат. Все же девяносто.

Календарь

Олег Давыдов

Колесо Екатерины

Ток страданий, текущий сквозь время

7 декабря православная церковь отмечает день памяти великомученицы Екатерины Александрийской. Эта святая считалась на Руси покровительницей свадеб и беременных женщин. В её день девушки гадали о суженом, а парни устраивали гонки на санках (и потому Екатерину называли Санницей). В общем, это был один из самых весёлых праздников в году. Однако в истории Екатерины нет ничего весёлого.

Ив Фэрбенкс

Нельсон Мандела, 1918-2013

5 декабря 2013 года в Йоханнесбурге в возрасте 95 лет скончался Нельсон Мандела. Когда он болел, Ив Фэрбенкс написала эту статью о его жизни и наследии

Достижения Нельсона Ролилахлы Манделы, первого избранного демократическим путем президента Южной Африки, поставили его в один ряд с такими людьми, как Джордж Вашингтон и Авраам Линкольн, и ввели в пантеон редких личностей, которые своей глубокой проницательностью и четким видением будущего преобразовывали целые страны. Брошенный на 27 лет за решетку белым меньшинством ЮАР, Мандела в 1990 году вышел из заточения, готовый простить своих угнетателей и применить свою власть не для мщения, а для создания новой страны, основанной на расовом примирении.

Молот ведьм. Существует ли колдовство?

5 декабря 1484 года началась охота на ведьм

5 декабря 1484 года была издана знаменитая «ведовская булла» папы Иннокентия VIII — Summis desiderantes. С этого дня святая инквизиция, до сих пор увлечённо следившая за чистотой христианской веры и соблюдением догматов, взялась за то, чтобы уничтожить всех ведьм и вообще задушить колдовство. А в 1486 году свет увидела книга «Молот ведьм». И вскоре обогнала по тиражам даже Библию.

Александр Головков

Царствование несбывшихся надежд

190 лет назад, 1 декабря 1825 года, умер император Александра I, правивший Россией с 1801 по 1825 год

Александр I стал первым и последним правителем России, обходившимся без органов, охраняющих государственную безопасность методами тайного сыска. Четверть века так прожили, и государство не погибло. Кроме того, он вплотную подошёл к черте, за которой страна могла бы избавиться от рабства. А также, одержав победу над Наполеоном, возглавил коалицию европейских монархов.

Интервью

«Музыка Земли» нашей

Пианист Борис Березовский не перестает удивлять своих поклонников: то Прокофьева сыграет словно Шопена – нежно и лирично, то предстанет за роялем как деликатный и изысканный концертмейстер – это он-то, привыкший быть солистом. Теперь вот выступил в роли художественного руководителя фестиваля-конкурса «Музыка Земли», где объединил фольклор и классику. О концепции фестиваля и его участниках «Частному корреспонденту» рассказал сам Борис Березовский.

Андрей Яхимович: «Играть спинным мозгом, развивать анти-деньги»

Беседа с Андреем Яхимовичем (группа «Цемент»), одним из тех, кто создавал не только латвийский, но и советский рок, основателем Рижского рок-клуба, мудрым контркультурщиком и настоящим рижанином – как хороший кофе с черным бальзамом с интересным собеседником в Старом городе Риги. Неожиданно, обреченно весело и парадоксально.

«Каждая собака – личность»

Интервью со специалистом по поведению собак

Антуан Наджарян — известный на всю Россию специалист по поведению собак. Когда его сравнивают с кинологами, он утверждает, что его работа — нечто совсем другое, и просит не путать. Владельцы собак недаром обращаются к Наджаряну со всей страны: то, что от творит с животными, поразительно и кажется невозможным.

Юрий Арабов: «Как только я найду Бога – умру, но для меня это будет счастьем»

Юрий Арабов – один из самых успешных и известных российских сценаристов. Он работает с очень разными по мировоззрению и стилистике режиссёрами. Последние работы Арабова – «Фауст» Александра Сокурова, «Юрьев день» Кирилла Серебренникова, «Полторы комнаты» Андрея Хржановского, «Чудо» Александра Прошкина, «Орда» Андрея Прошкина. Все эти фильмы были встречены критикой и зрителями с большим интересом, все стали событиями. Трудно поверить, что эти сюжеты придуманы и написаны одним человеком. Наш корреспондент поговорила с Юрием Арабовым о его детстве и Москве 60-х годов, о героях его сценариев и религиозном поиске.

Почему всё вокруг такое, какое оно есть?

Почему всё вокруг такое, какое оно есть?

Беллур Сиварамия ЧАНДРАСЕКАР

Окончание. См. № 2, 4,
6, 8, 10,
12, 16, 18,
20, 22/05

12. Сверхпроводники (окончание)

3. Ключи к разгадке

Объяснение явления сверхпроводимости
стало одним из самых впечатляющих достижений
физики. Оно представляет собой красивое
объединение некоторых идей физики твёрдого тела,
уже описанных в этой книге: квантовой механики
электронов в твёрдых телах, фононов, природы
электропроводности, явлений, связанных с
магнитным полем. Перечислим основные факты и
отметим, чем они могут быть полезны для
объяснения явления. При этом мы не будем
следовать истории вопроса и опишем ситуацию так,
как она представляется сегодня.

1. В противоположность ферромагнетизму
сверхпроводимость – довольно обычное явление:
известны сотни сверхпроводников, явление
наблюдается у веществ с разнообразной
кристаллической структурой и химическим
составом. Единственным общим свойством этих
веществ, помимо сверхпроводимости, является то,
что выше своей температуры перехода они являются
металлическими проводниками. Поэтому следует
искать объяснение сверхпроводимости в каких-то
весьма общих для таких проводников свойствах,
которые не зависят от их кристаллической
структуры и химического состава.

2. В большинстве случаев температуры
перехода ниже 100 К. Напоминаем, что температура
есть мера тепловой энергии системы. Средняя
кинетическая энергия электронов проводимости в
металле, выраженная в единицах температуры,
порядка 100 000 К. Таким образом, те энергии, которые
соответствуют явлению сверхпроводимости,
составляют крохотную долю полной энергии
электронов. Возникает образ поиска иголки в
стоге сена.

3. Средние энергии фононов близки к
энергиям, отвечающим температуре перехода.
Поэтому можно полагать, что фононы как-то
участвуют в игре. Эта мысль усиливается тем
фактом, что температуры переходов разных
изотопов одного вещества почти не отличаются
друг от друга, а мы знаем, что изотопы отличаются
именно своей фононной, а не электронной
структурой.

4. Тот факт, что переносчиками
сверпроводящего тока являются пары электронов,
наводит на мысль, что мы должны искать тот «клей»,
который связывает электроны в пары.

5. Напомним, что теплота в металлах
переносится главным образом электронами и
дырками, которые благодаря своей тепловой
энергии находятся в состояниях, слегка поднятых
над энергией Ферми (рис. 12-6). Плохая
теплопроводность сверхпроводников означает, что
в эти состояния попадает меньше электронов по
сравнению с нормальным металлом. Это может
произойти, если между энергией Ферми и энергией
наинизшего доступного состояния тепловых
электронов существует щель (рис. 12-7). Если такая
щель возникает в момент перехода в
сверхпроводящее состояние, то в этом состоянии
оказывается меньше электронов, способных
переносить тепловую энергию, по сравнению с
числом таких электронов в нормальном металле. В
результате сверхпроводник оказывается плохим
проводником тепла и обладает малой
теплоёмкостью.

Вопрос. Почему у изотопов разная
фононная структура?

Ответ. У изотопов разные массы ядер,
следовательно, разные атомные массы. Фонон –
квант колебательной энергии атома в твёрдом
теле, так что эти энергии у атомов с разными
массами различны.

4. Куперовские пары и теория БКШ

Физик Леон Купер показал, каким
образом определённого типа взаимодействие между
электронами может привести к образованию пар
связанных электронов, обладающих
противоположными значениями импульсов и спинов.
Такие пары получили название куперовских пар.
Эти пары – очень необычные объекты. Это не просто
два электрона, как-то привязанных друг к другу,
так что они находятся рядом и движутся как единое
целое, т.е. нечто вроде электронной молекулы,
состоящей из двух электронов, например как
молекула кислорода, состоящая из двух связанных
друг с другом атомов. На самом деле два электрона
сами по себе не могут образовать связанное
состояние, т.к. электрическая сила отталкивания
одноимённых зарядов заставит их разлететься в
разные стороны. Нужен какой-то посредник, чтобы
отталкивание сменилось притяжением. Примером
такого посредника является ядро гелия, которое
удерживает два электрона на близком расстоянии
друг от друга. Это происходит потому, что
притяжение к положительно заряженному ядру
больше, чем отталкивание электронов друг от
друга. Можно сказать, что пара электронов в атоме
гелия тесно связана и требуется конечная
энергия, чтобы её разорвать. Это та энергия,
которая может оторвать электрон от атома гелия,
образовав ион.

Посредник, объединяющий два электрона
в куперовскую пару, – это фонон, квант энергии
тепловых колебаний атомов в твёрдом теле.
Покажем, как это происходит (рис. 12-8). Два
электрона А и В приближаются друг к другу,
двигаясь в противоположных направлениях с
фермиевской скоростью. Электрон А испускает
фонон и начинает двигаться в другом направлении.
Электрон В поглощает фонон и изменяет свой
импульс на ту же величину, что и А, но
направленную в противоположную сторону, так что
оба электрона продолжают двигаться, но теперь
разлетаются в противоположных направлениях.
Пара остается невредимой, но связанной, так
сказать, фононом. Это и есть куперовская пара.
Такой процесс происходит со всеми парами
электронов, двигающихся с противоположно
направленными скоростями вблизи всей
поверхности Ферми, так что в результате
возникает сверхпроводящее состояние. Напомним,
что импульс равен массе, умноженной на скорость,
поэтому куперовская пара представляет собой два
электрона с противоположными импульсами (и
следовательно, с нулевым полным импульсом),
связанных за счёт испускания и поглощения
фонона. Спины двух электронов также
противоположно направлены – это проверено на
эксперименте и предсказывается теорией.

Вопрос. Каким образом электрон
испускает и поглощает фонон?

Ответ. Отрицательный заряд электрона
притягивает к себе окружающие положительно
заряженные ионы, создавая локальное увеличение
давления. Нечто подобное происходит в звуковой
волне. Можно говорить об испускании фонона
электроном. Через промежуток времени, равный
половине периода звуковой волны, сжатие
переходит в локальное расширение
кристаллической решётки. Если в этот момент
рядом окажется второй электрон, он притягивает
(за счёт электрических сил) ионы к исходным
положениям, что соответствует поглощению фонона.

Итак, мы представляем, как образуются
куперовские пары за счёт посредничества фононов.
Но происходит не просто образование пар.
Оказывается, что энергия электронов в такой паре
меньше, чем энергия этих же электронов,
движущихся независимо. Когда электрон А создаёт
и испускает фонон, он тянет к себе окружающие
соседние ионы за счёт электрической силы
притяжения между отрицательным зарядом
электрона и положительным зарядом иона.
Напомним, что фонон – это волна сжатия в твёрдом
теле. Поэтому потенциальная энергия электрона
меньше, чем она была бы, если бы ионы остались в
невозмущённых положениях. Электрон В, приходящий
в это место через половину периода фононной
волны, «видит» эти ионы на большем расстоянии от
себя, чем они были бы без учёта расширения
решётки. Поэтому энергия электрона В возрастает.
Однако это возрастание меньше, чем уменьшение
энергии электрона А. В итоге энергия куперовской
пары меньше, чем сумма энергий независимо
движущихся электронов. Разность между этими
энергиями и есть энергия связи куперовской пары.
Чтобы разрушить пару, нужно затратить эту
энергию. Мы описали образование куперовских пар.
В сверхпроводнике все электроны вблизи
поверхности Ферми «спариваются» таким образом
при абсолютном нуле температуры. Следует
заметить, что образование пары требует двух
электронов, которые переходят из начального
состояния в конечную пару состояний за счёт
испускания и поглощения фонона. Но это возможно
только в том случае, если конечная пара состояний
свободна, не занята другими электронами.
Напомним, что электроны – фермионы, так что в
заданном состоянии не может быть более одного
электрона.

Из последнего замечания вытекает, что
образование куперовских пар зависит от того, что
делают все другие электроны. Имеется сильная
корреляция между куперовскими парами, они не
являются независимыми объектами. Приведём
грубую аналогию: электроны в нормальном металле
похожи на молекулы газа, все они движутся
независимо. Электроны в сверхпроводнике похожи
на молекулы в кристалле. Все эти молекулы сильно
коррелированы друг с другом, так что кристалл
может двигаться только как единое целое, а не как
собрание независимых молекул. Точно так же, как
говорят о конденсации газа молекул с
образованием кристалла, можно говорить и о
конденсации электронов в сверхпроводнике в
новое состояние – сверхпроводящее. Аналогия
очень грубая: молекулы в кристалле
конденсируются в упорядоченное состояние в
отношении своих положений, чего не происходит в
сверхпроводнике. Электроны в сверхпроводнике
конденсируются в упорядоченное состояние по
отношению к своим импульсам. Но в аналогии есть
ещё нечто общее. Атомы газа обладают импульсами,
т.к. они движутся, в то время как атомы в кристалле
неподвижны (если не считать тепловых колебаний) и
их импульс равен нулю. Электроны в нормальном
металле также движутся с ненулевыми импульсами,
в то время как каждая куперовская пара в
сверхпроводнике имеет нулевой импульс и, по
существу, покоится. Кристалл может двигаться
только как единое целое, и каждая молекула в нём
совершает то же движение, что и весь кристалл.
Одна из молекул может иметь другую скорость,
только если её вытеснили из кристалла, а это
требует определённого количества энергии.
Аналогично, все куперовские пары в
конденсированном состоянии движутся как единое
целое и, чтобы выбить из пары отдельный электрон,
нужно затратить энергию, равную энергии связи
пары.

На рис. 12-9 показано, в чём состоит
разница между нормальным и сверхпроводящим
состояниями металла. Разглядывая рисунок,
представьте, что отдельные электроны во всех
случаях разлетаются в разные стороны, но
куперовские пары либо неподвижны (нулевой ток),
либо имеют общую (с током) скорость. В нормальном
металле нужно в принципе проследить за путём
каждого электрона, чтобы понять поведение
металла. В сверхпроводнике достаточно знать
поведение всего лишь одной куперовской пары –
все остальные ведут себя точно так же.

Теперь можно понять, почему
электрический ток в сверхпроводнике течёт, не
испытывая сопротивления. Ток переносится
куперовскими парами, движущимися с одинаковой
скоростью. Электрическое сопротивление
возникает в результате рассеяния друг на друге
независимо движущихся электронов. Если
конденсату куперовских пар передаётся некоторая
минимальная энергия, то из него выбрасываются
такие свободные электроны. Если электрический
ток достаточно большой, то необходимую энергию
можно получить за счёт кинетической энергии
движения пар. В этом случае энергия будет
затрачена на разрушение пар, после чего
восстановится нормальное сопротивление. Таким
образом, становится понятным, почему ток в
сверхпроводнике не может превышать некоторое
максимальное значение, называемое критическим
током. По достижении этого тока
сверхпроводимость разрушается и металл
становится нормальным.

Описанная выше картина
сверхпроводимости была предложена физиками
Джоном Бардином, Леоном Купером и Робертом
Шриффером и стала известной как теория БКШ. Эти
учёные и их последователи показали, что
детальная разработка следствий такой картины
объясняет все наблюдаемые свойства
сверхпроводников. Теория БКШ явилась одним из
величайших достижений квантово-механического
описания природы. Первоначально она была
разработана для того, чтобы показать, каким
образом огромное число электронов в металле
может влиять друг на друга за счёт обмена
фононами и образовывать сверхпроводящее
состояние. Но значение теории БКШ много больше,
т.к. она показывает, как следует рассматривать
взаимодействующие друг с другом фермионы. Теорию
БКШ использовали, например, для объяснения
свойств атомных ядер, в которых фермионами
являются протоны и нейтроны, и ряда
астрономических объектов, называемых
нейтронными звёздами, которые состоят из очень
плотно упакованных нейтронов.

5. Джозефсоновские переходы

Физик Брайан Джозефсон, использовав
теорию БКШ, предсказал явление, которое вскоре
действительно было обнаружено и получило его
имя. Пусть два сверхпроводника А и В разделены
тонкой изолирующей прослойкой С (рис. 12-10),
образуя контакт. К образцам А и В подключена
батарея, так что к ним приложено напряжение U.
Прослойка С достаточно тонкая, и через неё может
протекать определённый, пусть и маленький, ток.
Если вся остальная часть установки (не
показанная на рисунке) собрана должным образом,
то обнаруживается, что контакт испускает фотоны
(электромагнитные волны) частотой  f = 2eU/h, где е
– заряд электрона, а h – постоянная Планка. При
заданном напряжении частота  f  зависит
только от двух универсальных констант и не
зависит от конкретных свойств используемых
сверхпроводников. Это весьма примечательный
результат! Явление следует исключительно из
самого факта существования куперовских пар
(отсюда множитель 2е в формуле для частоты) и
законов квантовой механики (отсюда постоянная
Планка h)!

Возникновение эффекта Джозефсона
можно понять, вспомнив некоторые основные
принципы квантовой механики. Сверхпроводящее
состояние обусловлено существованием
куперовских пар с нулевым импульсом (когда тока
нет) или некоторым ненулевым, но одинаковым для
всех пар (когда течёт сверхпроводящий ток
конечной величины). Такое состояние можно
описать волновой функцией. Сейчас нам не важно,
какова точная форма этой функции. Важно, что у
этой функции есть часть, определяющая, чему равна
энергия и скорость (или, эквивалентно, частота и
длина волны) каждой куперовской пары. Обе
указанные величины определяют осцилляции
волновой функции во времени (частота) и в
пространстве (длина волны). Оба осциллирующих
свойства можно объединить в единую величину,
которая называется фазой и представляет
попросту угол (рис. 12-11). Фаза обладает следующими
свойствами, вытекающими из того, что она есть
часть волновой функции:

1. Частота осцилляций f непосредственно
связана с энергией квантово-механической
формулой E = hf.

2. Если в двух точках образца фазы
различны, то между этими точками должен
наблюдаться поток вещества. Если разность фаз
постоянна во времени, то поток также постоянен.
Но если разность фаз осциллирует во времени, то и
поток осциллирует.

Посмотрим, как эти свойства отражаются
на поведении джозефсоновского перехода,
изображённого на рис. 12-10. Между
сверхпроводниками А и В по обеим сторонам
диэлектрического слоя имеется напряжение U.
Потенциальная энергия заряда равна величине
заряда, умноженной на приложенное напряжение.
Разность напряжений для куперовских пар в А и В
равна U В. Поэтому энергии куперовских пар
зарядом 2е в этих сверхпроводниках отличаются на
величину 2еU. Это означает, что разность фаз между
двумя сверхпроводниками осциллирует с частотой f
= 2eU/h.

Наличие такой осциллирующей фазы в
свою очередь означает, что между
сверхпроводниками А и В течёт переменный ток той
же частоты. Как мы знаем, переменный ток является
генератором фотонов той же частоты. Именно это и
наблюдается, и называется эффектом Джозефсона.

Одна сторона эффекта Джозефсона
особенно поразительна. Фундаментальным
следствием основных законов квантовой механики
является то, что частота волновой функции
определяется энергией системы. Во многих
случаях, о которых шла речь выше, эта частота явно
не проявляется в экспериментах. Но в эффекте
Джозефсона мы можем, что называется, руками
пощупать эту величину, измерив в лаборатории
частоту электромагнитных волн (фотонов). Таким
образом, существование эффекта Джозефсона
полностью рассеивает длительные сомнения
относительно реальности волновых функций и
справедливости законов квантовой механики.

6. Сверхпроводники за работой

Наиболее важным практическим
применением сверхпроводников до сих пор было
создание электромагнитов – катушек из
сверхпроводящей проволоки с током. Проволоку
делают из сплава ниобия и титана. Такой материал
становится сверхпроводником при температуре
ниже 11 К. Сам магнит нужно охлаждать в жидком
гелии при температуре 4 К, но установку
конструируют так, чтобы магнитное поле было
доступно в некотором объёме при комнатной
температуре. Подобные магниты используются в
ЯМР-установках для медицинской диагностики и в
ускорителях элементарных частиц, где необходимы
очень сильные магнитные поля.

До того как сверхпроводящие магниты
стали практичными и доступными, использовались
обычные электромагниты – железный сердечник с
намотанной на него медной проволокой. Медь –
хороший проводник, но всё же обладает
сопротивлением. Поэтому при прохождении тока
катушка нагревается: электрическая энергия
превращается в тепловую. Это явление имеет два
нежелательных следствия – существенные затраты
электроэнергии и ограниченность создаваемого
магнитного поля. Выделяемую теплоту необходимо
как-то отводить, в противном случае магнит может
расплавиться.

В сверхпроводящем магните проволока
имеет нулевое сопротивление, поэтому
электрический ток вообще её не нагревает.
Критические магнитные поля в используемых
сплавах очень высоки, поэтому современные
сверхпроводящие магниты создают намного более
сильные поля без существенных затрат энергии.
Пока что это самое успешное практическое
применение сверхпроводимости. Существуют
предложения по использованию сверхпроводников в
других областях техники. Примерами могут служить
сверхпроводящие кабели для передачи
электроэнергии и джозефсоновские переходы в
электронных устройствах. Поиски продолжаются.

Сокр. пер. с англ. А.В.БЕРКОВА
[email protected]

Теория винтовой пары — Энциклопедия по машиностроению XXL

Теория винтовой пары  [c.22]

Основы теории винтовой пары (типы резьб, основные параметры, силовые соотношения, к. п. д. и др.) были изложены в 3.1 и 3.2.  [c.472]

ТЕОРИЯ ВИНТОВОЙ ПАРЫ  [c.32]

Основы теории винтовой пары (типы резьб, силовые и кинематические зависимости, к. п. д. и др.) были изложены в гл. 1 Резьбовые соединения . Ниже излагаются только некоторые дополнительные сведения.  [c.298]

Исключен раздел Прикладная механика , имевшийся в первом издании. Краткие сведения из теории механизмов и машин включены частично в раздел Теоретическая механика (в виде отдельной главы), частично — в соответствующие главы раздела Детали машин последнее относится, в частности, к силовым соотношениям в винтовых парах и к основным понятиям геометрии зубчатого зацепления.  [c.3]

Энергия дислокации по-прежнему будет выражаться формулой (14.5.1), но компоненты напряжения в этой формуле определяются в результате решения задачи теории упругости с удовлетворением граничным условиям поэтому величина энергии будет зависеть от положения дислокации в теле. Здесь мы рассмотрим простейший пример — винтовую дислокацию в круговом цилиндре бесконечной длины, ось которой параллельна оси цилиндра, но не совпадает с ней. Пусть будет радиус цилиндра Л, расстояние винтовой дислокации от оси O i = р. Проведем ось xi через центр сечения и ось дислокации, как показано на рис. 14.8.1, и поместим вторую дислокацию противоположного знака в точке Сй, находящейся на оси xj на расстоянии Л /р от начала координат. По формулам (14.4.2) напряжения в неограниченной среде для такой пары дислокаций выражаются следующим образом  [c.469]

Мгновенная винтовая ось. Касательное винтовое движение. Значения скоростей различных точек твердого тела таковы, как если бы тело совершало либо одно вращательное Ош и одно поступательное движение ОУ , либо три одновременных вращения вращение Ош и два вращения ш и —ш , образующих пару с вектором моментом ОУ . Согласно правилу, установленному в теории сложения вращений, это распределение скоростей будет в то же время таким, как если бы тело совершало одно винтовое движение вокруг центральной оси системы вектора ш, ш°, —ш°. Уравнения этой центральной оси получатся, если искать геометри-  [c.72]

Анализируя (5.2) при разных значениях шага т, были определены неустойчивые моды (рис. 6), которые оказались более реалистичными для анализа существования равновесных конфигураций реальных вихревых структур, чем решение для системы из точечных вихрей [И]. С целью проведения сопоставления между системами с разным числом вихрей для сохранения суммарной интенсивности в системе размер вихрей выбирался так, чтобы суммарная площадь сечений ядер вихрей была одинаковой, т. е. е = 0.15л/]У. В результате заметим, что учет винтовой формы вихрей с уменьшением их шага приводит к потере устойчивости вихревыми системами все для меньшего и меньшего их числа, а при т устойчивые конфигурации из винтовых вихрей отсутствуют полностью. Качественно это согласуется с результатами визуальных наблюдений и снимет отмеченное во введении противоречие их сравнения с данными теории равновесия точечных вихревых систем. Более того, экспериментальные результаты работы [3] позволяют провести и количественное сравнение. В [3] описана двойная вихревая структура N = 2 с безразмерным шагом т = 1.45. Этот режим хоть и близок к границе неустойчивости (см. диаграммы рис. 6), но является еще устойчивым, т.е. такая вихревая пара существовать может. А близость ее параметров к границе неустойчивых режимов косвенно подтверждается тем, что получить ее в эксперименте было очень трудно, требовалась тонкая регулировка экспериментальной установки и режимных параметров течения для получения вихревой пары с параметрами, обеспечивающими ее устойчивой существование.  [c.412]

Один из вероятных механизмов образования мартенситного зародыша в аустените, предложенный А. С. Франком [26—28, 6] с позиций теории дислокаций, предусматривает две следующие одна за другой деформации решетки исходной фазы. Первая представляет собой однородный сдвиг в плоскости габитуса (111), который в первом приближении можно рассматривать как следствие движения линейной дислокации (длина последней может достигать 10 —10 параметров кристаллической решетки). Благодаря этому первичному сдвигу образуется превращенная поверхность раздела значительной ширины и длины. Вторую неоднородную деформацию он рассматривает как результат движения рядов винтовых дислокаций по превращенной поверхности раздела, которые расположены в одной из шести пар плоскостей (011). Каждый дислокационный блок скольжения этих шести плоскостей смещает соседний на одно межатомное расстояние. В пределах каждого блока сдвиг плоскостей происходит на одну шестую часть расстояния и является однородным, а общий вектор Бюргерса этого вторичного сдвига в пределах блока равен нулю.  [c.18]

Выращивание кристаллов путем конденсации паров предполагает наличие температурного градиента между источником пара, имеющего обычно более высокую температуру, и пространством, где происходит рост кристаллов. Температуры источника паров и кристалла являются важнейшими параметрами процесса роста, и скорость роста, которая определяется степенью пересыщения, можно легко контролировать путем подбора этих температур. Рост кристаллов происходит с заметной скоростью при степени пересыщения порядка 0,1% в то время как, согласно теории образования ядер, степень пересыщения должна была бы составлять несколько десятков процентов. Как уже говорилось, такое несоответствие объясняется наличием винтовых дислокаций или других дефектов на поверхности кристалла. Этим методом можно просто и эффективно выращивать монокристаллы многих металлов, неорганических и органических соединений.  [c.204]

Передачу винт—гайка служит для преобразования вращательного движения в иоступачельное. Основы теории винтовой пары (тииьг резьб, силовые и кинематические зависимости, к. п. д. и др.) изложены fs гл. 1 Резьбовые соединения . Ниже излагаются только некоторые доиоли1ГРельные сведения.  [c.257]

Передача винт — гайка служит для преобразования вращательного движения в поступательное. Основы теории винтовой пары (типы резьб, силовые и киневиатические зависимости, КПД и др.) изложены в гл. 1. Ниже излагаются только некоторые дополнительные сведения.  [c.310]

На рубеже XIX и XX столетий Ф. Рело еще раз сделал попытку отвоевать для кинематики утраченные ею позиции. В 1900 г. он опубликовал второй том своей Теоретической кинематики , правда, под измененным названием ( Учебник кинематики , т. 2). По существу в этой работе содержалось не развитие прежних идей автора, опубликованных им в 1875 г., а их новая трактовка. Рело своеобразно и очень детально развил теорию кинематических пар, перестроил аналитическую кинематику механизмов, а также попытался связать методы исследования механизмов с подобием в их построении. Он выделил шесть групп механизмов, служащих для передачи движения,— винтовые механизмы, механизмы шарнирно-звеньевые, колесные (фрикционные и зубчатые), кулачковые, стопорные и механизмы, в состав которых входят гибкие передачи. Подобной классификацией с теми или иными видоизменениями пользуются и в настоящее время. Рело сделал также попытку построить теорию рабочих машин с помощью теории кинематических пар, однако она не была замечена современниками и не получила дальнейшего развития.  [c.84]

Теория винтов возникла в начале прошлого столетия после появления работ Пуансо, Шаля и Мебиуса, изучавших теорию пар сил и бесконечно малых враш,ений и впервые установивших аналогию силы и бесконечно малого враш,ения. В работах этих авторов установлена эквивалентность произвольного перемеш,ения тела винтовому перемещению и положено начало изучению кинематики и статики, а также сформировано понятие винта, которое в дальнейшем развито в работах Плюккера.  [c.3]

Теория пар сил — fiziku5.ru

Могут использоваться 2 или 3 уравнения моментов.

Пример

Составим уравнение суммы всех сил на ось X и Y:

Сумма моментов всех сил относительно точки А:

Параллельные силы

Уравнение относительно точки А:

Уравнение относительно точки В:

Сумма проекций сил на ось У:

Теория пар сил

Система двух равных по модулю параллельных противоположно направленных сил, называется парой сил.

Пара не имеет равнодействующую, её можно уравновесить только другой парой и можно представить в виде вектор-момента.

Свойства пар сил

1)  Пару сил можно переносить в плоскости её действия произвольно, не изменяя её действие.

2)  Момент пары не зависит от выбора центра.

Покажем, что сумма моментов сил относительно любого центра не зависит от выбора центра и равняется сумме момента.

Теорема об эквивалентности. Сложение пар сил в пространстве

Две пары, имеющие равные моменты – эквивалентны.

Продолжим векторы и отметим точки A и B.

Следовательно, две пары, имеющие равные моменты эквивалентны.

Можно произвольно менять модули сил и плечо пар, сохраняя неизменными их момент.

Перенос пары в параллельную плоскость

Пло­скости I и II должны быть параллельны, в частности, они могут совпадать.

Если приложить и и совместить точки при­ложения сил с проекциями точек, то получим:

Силы равны по модулю, поэтому их рав­нодействующие R и R’ должны быть приложены в точке пересече­ния диагоналей прямоугольника ABB1A1, кроме того, они равны по модулю и направлены в проти­воположные стороны. Это означает, что они составляют систему, экви­валентную нулю.

Таким образом:

1)  Пару сил можно переносить в параллельную плоскость. Произвольно менять модули сил и плечо, сохраняя момент. Две пары можно привести к одному плечу.

2)  Пару сил можно перемещать в плоскости её действия.

Вектор – момент пары можно считать свободным вектором.

Если не плечо действует система пар сил, то складывая их геометрически получим главный вектор – момент равнодействующей пары, равный сумме векторов.

Понятие о статическом равновесии конструкции

Составляется уравнение относительно точки опрокидывания конструкции

– вес стены

Точка А – точка возможного опрокидывания

Муд=1,5Мопр

Мопр – момент опрокидывающий

Муд – удерживающий момент

Приведение силы к произвольному центру по методу Пуансо

Чтобы эффект действия сохранился нужно добавить равную и противоположную силу , которая образует присоединенную пару с плечом AB.

В результате приведения получаем силу , равную исходной и присоединенную пару.

с моментом M=Fh, можно представить в виде вектор – момента.

Так как вектор – момент свободный вектор, то его так же можно построить в точке B. Следовательно получаем: , которые можно приложить в точку B.

Применяя метод Пуансо к системе сил, произвольно расположенных в пространстве можно получить условие равновесия любой произвольной системы в пространстве.

Приведение пространственной системы сил к произвольному центру.

Условия равновесия пространственной системы

Требуется привести силы с центром О, с которым свяжем систему координат. Переносим F1 в точку О, прикладываем , которая образует пару, проделываем то же с F2.

Т. к. вектор-моменты пар являются параллельными векторами все их можно приложить к точке О.

Складывая их геометрически получим главный вектор момент:

Складывая F1, F2, Fn получаем главный вектор:

Ориентация векторов может быть определена с помощью косинусов.

Любую произвольную систему сил можно привести к любому центру и заменить двумя векторами M и R.

Final Theory в Steam

Об этой игре

Описание

Final Theory — это пошаговая стратегическая игра в 4X-lite, в которой вы управляете флотом линкоров, участвующих в галактической гражданской войне. Это захватывающий опыт как для опытных игроков, так и для новичков в этом жанре. Он отличается инновационной боевой механикой, но также напоминает некоторые из классических игр.

Особенности

• Пошаговая стратегия.
• Инновационная боевая система с шестигранной сеткой.
• 6 уровней сложности, подходящих как для новичков, так и для ветеранов.
• 7 различных типов кораблей для управления.
• 8 уровней кораблей с оружием, способностями и очками навыков.
• 56 обновлений модуля на выбор.
• Быстрые и нестандартные сражения. Поддерживает PvP через удаленную игру вместе
  Развертывайте свои корабли и сражайтесь с друзьями.

Предыстория: Галактическая империя находится в состоянии распада из-за острой нехватки ее важнейшего ресурса.Без этого ресурса миллионы колоний будут отрезаны от космоса и неизбежно вернутся к более примитивному состоянию. Империя объявила территории внешнего кольца безнадежным делом, и теперь каждый сектор галактики готовится к войне. Отчаявшись поддерживать свой образ жизни любыми необходимыми средствами.

Архивы говорят о старом исследовательском проекте, который проводился на пике процветания империй. Боеголовка, способная вызвать каскадный коллапс подпространства в центре галактики и создать несравненное богатство.Достаточно, чтобы обеспечивать галактику на бесчисленные эоны и допускать подпространственные прыжки на ранее невообразимые расстояния. Кодовое название этого проекта было Final Theory.

Предполагаемой целью такого оружия было вступление в эпоху межгалактической колонизации, но в конечном итоге проект был заброшен. Риск считался слишком большим, поскольку неконтролируемый каскад такой величины мог оказаться разрушительным для галактики.

Однако данные проекта остаются. Расположен на старых исследовательских станциях, разбросанных по галактике.Восстановление этих данных стало последней надеждой для покинутых колоний внешней границы. Вам, как командиру вновь образованного владения, предстоит преодолеть эти темные времена и обеспечить будущее своему народу.

ЗАКЛЮЧИТЕЛЬНАЯ ТЕОРИЯ Copyright © 2018 Monticube. Все права защищены.

,

Теория хаоса в Steam

«Chaos Theory — очень амбициозный проект с огромным размахом, поэтому, чтобы помочь нам воплотить его в жизнь, мы решили перейти в ранний доступ, чтобы собрать вместе достаточное количество людей и запустить следующий этап разработки в полную силу.

Имейте в виду, что, поскольку мы находимся на очень раннем этапе доступа, вероятно, будут некоторые ошибки, которые мы постараемся исправить с вашей помощью. Вдобавок, поскольку у нас очень большие возможности для этой игры, мы будем периодически выпускать обновления с все большим количеством функций, когда нам позволяют время и ресурсы.»

«Поскольку возможности Chaos Theory очень велики, и мы не хотели бы выпускать игру до того, как она будет полностью реализована и протестирована, мы не можем быть слишком точными в отношении даты выхода из раннего доступа, однако чем больше людей мы будем поддерживать тем быстрее мы сможем вывести игру из раннего доступа в полностью выпущенную игру.

Сказав, что мы действительно хотели бы получить приблизительную оценку того, когда игра может выйти из раннего доступа, которая будет выглядеть осенью 2019 года.»

«Полная версия Chaos Theory будет полнофункциональной со всеми аспектами нашего первоначального объема. Однако объем может измениться, чтобы включить дополнительные функции, но мы постараемся сделать первый первоначальный выпуск полностью функциональной и игровой без ошибок и полностью сбалансированной игровой механикой.

Хотя некоторые из нижеперечисленных будут включены в выпуск раннего доступа по мере их разработки, здесь представлены некоторые из полных функций;

• Полностью интерактивная среда
• Сложный и запутанный ИИ и социальная система
• Создавайте и создавайте множество предметов
• Создавайте и стройте здания
• Полностью реализованная боевая система
• Режим Бога
• Многопользовательский режим

”

«Имейте в виду, что Chaos Theory в настоящее время находится в очень раннем доступе, и если вы купите игру, вы станете частью важной группы игроков, которые помогут формировать и развивать игру, чтобы полностью раскрыть ее потенциал.Однако все функции, перечисленные в разделе «Об этом», будут доступны для вас в раннем доступе, и когда будет добавлено больше функций, мы обновим этот раздел, чтобы отразить.

Изначально Chaos Theory будет находиться в тестовом режиме песочницы с некоторыми базовыми функциями, которые позволят вам играть в игру. Однако имейте в виду, что в данный момент сохраненные игры недоступны ».

«Цены, вероятно, останутся прежними, однако мы включим некоторые бесплатные функции для тех, кто решил приобрести игру в раннем доступе после ее полного выпуска.»

«Мы очень серьезно относимся к мнениям и отзывам нашего игрового сообщества, поэтому мы дадим всем нашим игрокам возможность в полной мере участвовать в будущем развитии игры. В некоторых случаях мы позволим нашему сообществу поддерживать нас и оставлять отзывы по электронной почте, с помощью механизмов обратной связи в игре и на нашей странице форума ».

,

Global Cold War в Steam

Об этой игре

ИСТОРИЯ

От создателей отмеченной наградами научно-фантастической игры Out There …

В ближайшем будущем над миром нависает научное открытие, меняющее парадигму, обещающее радикально новые технологии. Мировые сверхдержавы понимают, что они могут иметь власть разрушить глобальную финансовую систему, стереть с лица земли целые страны или даже получить доступ к бессмертию.

Однако это открытие, получившее название «Теория сигмы», может быть использовано только горсткой ученых.Вы возглавили подразделение Sigma в вашей стране. Ваша цель — убедиться, что именно ваша нация извлекает выгоду из теории сигмы раньше всех остальных.

Для достижения этой цели в вашем распоряжении будут мощные ресурсы: кадры самых элитных тайных агентов в мире, передовые тактические дроны и, конечно же, ваши собственные навыки дипломатии и уловок.

Это — холодная война, в которой человечество должно столкнуться со своим будущим.

ИДЕАЛЬНОЕ МОДЕЛИРОВАНИЕ ШПИОНАГА

Пошаговый шпионаж: Используйте своих специальных агентов, чтобы доминировать в мире.Соблазнение, шантаж, манипуляции, промышленный шпионаж… Каждый удар ниже пояса разрешен и поощряется.
Динамическое повествование: Развивайте и управляйте своими отношениями с более чем 100 NPC: лобби, вооруженные группы, политики… Альянс, обман или убийство, на ваш выбор.
Полевые операции: Управляйте похищением ваших целей во время захватывающих погонь в величайших городах мира. Сдержанность или прямая конфронтация, жизнь вашего агента в ваших руках.

Набор
Во-первых, наберите команду из четырех специальных агентов из 50 уникальных разблокируемых персонажей для поддержки ваших миссий.У каждого своя история, мотивация и черты характера, которые определяют их поведение во время миссий.
Получите доступ к исследователю, солдату, хакеру, соблазнителю и другим архетипам, чтобы завершить свое подразделение Сигмы и выполнить свою стратегию.

Шпионаж
Когда ваша команда будет готова, назначьте им миссии по всему миру, чтобы собрать ученых, найти компрометирующие документы на местных политиков и многое другое.
Используйте способности своих агентов, чтобы соблазнять, манипулировать и подкупать ваших целей на свою сторону или нейтрализовать их.

Контрразведка
Другие страны также будут использовать своих агентов для проникновения в вашу страну и захвата ваших ученых. Отслеживайте, захватывайте и допрашивайте их, чтобы получить информацию о ваших врагах, а затем обменивайте их на выкуп, когда они больше не нужны.

Exfiltration
Прикажите своим агентам вывести ученых, привлеченных к вашему делу, во время пошаговых фаз эксфильтрации через крупнейшие столицы мира. Выбирайте позицию своих дронов с умом, чтобы выполнять эти сложные миссии.

Дипломатия
В теории сигм дипломатия — ключ к достижению ваших целей. Встречайтесь со своими зарубежными коллегами и добивайтесь своих целей, используя лесть, угрозы или шантаж. Вы также можете восстановить захваченных агентов, продолжить исследования и многое другое. Развивайте свои отношения с мощными лобби и вооруженными и влиятельными группами, чтобы добиться их расположения. Но будьте осторожны, они могут напасть на вас.

Дерево исследований
Теория сигмы является причиной этой холодной войны.Сплотите ученых со всего мира на свою сторону, чтобы открывать новые технологии, чтобы получить преимущество и изменить мир. Контроль над разумом, дестабилизация мировой экономики, роботы-солдаты, бессмертие… Вы сохраните эти открытия для себя или поделитесь ими с миром?

Игры, которые нас вдохновили:

XCom, Phantom Doctrine, Plague Inc, Pandemic (настольная игра), Rocket Ranger, Tropico, Armello, Civilization, любопытная экспедиция и многое другое.