Список парадоксов: Список парадоксов — Википедия (с комментариями)

Список парадоксов — это… Что такое Список парадоксов?

Это список парадоксов, сгруппированных по темам.

Парадо́кс (от др.-греч. παράδοξος — неожиданный, странный от др.-греч. παρα-δοκέω — кажусь) — ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения. Следует различать парадокс и апорию. Апория, в отличие от парадокса, является вымышленной, логически верной ситуацией (высказыванием, утверждением, суждением или выводом), которая не может существовать в реальности.

Логические (кроме математических)

Парадоксы самореференции (самоотносимости)

Это хорошо известный (и хорошо изученный) класс противоречий, возникающих в высказываниях, которые содержат определение чего-либо, неявно ссылающееся на само себя.

• Парадокс Берри: фраза «наименьшее число, которое нельзя описать менее, чем десятью словами» описывает это число девятью словами.
• Парадокс Карри: «Если это утверждение верно, то русалки существуют»
• Парадокс Эпименида: критянин говорит: «Все критяне — лжецы»
• Парадокс исключений (англ.): «Если у каждого правила есть исключения, то каждое правило должно иметь хотя бы одно исключение, кроме этого» …а это не исключение к правилу, которое утверждает, что у каждого правила есть исключения?
• Парадокс Греллинга-Нельсона (англ.): Является ли слово «гетерологичный», означающее «неприменимый к самому себе», гетерологичным словом? (Близко к Парадоксу Рассела.)
• Парадокс Гегеля: «История учит человека тому, что человек ничему не учится из истории»
• Парадокс лжеца: «Это предложение ложно».
• Y-комбинатор в лямбда-исчислении и комбинаторной логике был назван парадоксальным комбинатором так как он связан с самоотносимостью.
• Парадокс Петрония: «Ограничивайте себя во всех вещах, даже в ограничении».
• Парадокс Квина (англ.): «…влечёт за собой ложность, будучи добавленным к собственному цитированию» влечёт за собой ложность, будучи добавленным к собственному цитированию.
• «Парадокс Эватла» (софизм Эватла): Протагор взял ученика Эватла при условии, что тот ему заплатит, когда выиграет первое дело. Случилось так, что Протагор подал иск на Эватла за то, что тот ему долго не платит. Должен ли Эватл заплатить, если он выиграет это дело?
• Парадокс Рассела: содержит ли множество всех множеств, которые не содержат себя, само себя? Рассел популяризовал его в форме «парадокса брадобрея»: «Брадобрей бреет только тех людей, которые не бреются сами. Бреет ли он себя?»
• Парадокс Ришара: если сопоставить все свойства чисел с числами, то можно определить такое свойство, которому не будет соответствовать никакое число.
• Парадокс определения: невозможно дать определение определению, ибо пока мы не дали это определение, само понятие определения остается неизвестным.
• Прикажите слуге не слушаться Вас. Не слушаясь Вас, он ослушается приказа, так как он исполняет его, слушаясь Вас.
• Запрещено запрещать.
• Быть убеждённым в том, чтобы не иметь никаких убеждений.
• Советую Вам не слушать моих советов.
• Чем больше сыра, тем больше в нём дырок, но, ведь, чем больше дырок, тем меньше сыра. Получается, чем больше сыра, тем меньше сыра? (Алиса в зазеркалье)
• Чем больше самоубийц, тем меньше самоубийц.
• Чем больше мы учимся, тем больше мы знаем. Чем больше мы знаем, тем больше мы забываем. Чем больше мы забываем, тем меньше мы знаем. Зачем тогда учиться?
• Надпись на стене: «Долой надписи на стенах!».

^{[источник не указан 355 дней]}

Парадоксы определений

• Корабль Тесея: если каждый элемент корабля был заменён хотя бы один раз, можно ли считать корабль прежним кораблём?
• Парадокс кучи (англ.). В какой момент куча перестанет быть кучей, если отнимать от неё по одной песчинке?
• Парадокс лысого: если волосы с головы выпадают по одному, с какого момента человек становится лысым?
• Парадокс интересных чисел: наименьшее неинтересное натуральное число интересно само по себе этим фактом, но тогда оно не относится к неинтересным.

Математические и статистические

См. также: Категория:Математические парадоксы

• Парадоксы пропорционального представительства в США (en): некоторые системы представительства могут иметь последствия, идущие против интуиции:
• Парадокс голосования (Парадокс Эрроу/Arrow’s paradox (англ.)): нельзя совместить все требования к избирательной системе в одной системе.
• Закон Бенфорда: во многих списках чисел из произвольных реальных источников большинство чисел начинаются с цифры 1.
• Парадокс лифта: лифты чаще всего ходят в одном направлении — от середины здания вниз к подвалу и вверх к чердаку
• Парадокс ожидания: почему иногда приходится ждать автобус дольше, чем нужно. (пояснение смотрите в англ. статье Renewal theory)
• Игра в нетранзитивные кости (англ.): существует набор из 3 костей А, В и С таких, что чаще всего на А выпадает бо́льшее число, чем на В; на В чаще выпадает бо́льшее число, чем на С; на С чаще выпадает бо́льшее число, чем на А.
• Игра Пенни: нетранзитивный парадокс, разновидность игры в нетранзитивные кости.
• Парадокс Линдли (англ.): маленькие ошибки в нулевой гипотезе сильно возрастают, если анализируются большие массивы данных, приводя к ложным, но одновременно точным со статистической точки зрения результатам.
• Парадокс недоношенности (англ.): низкий вес при рождении и курение матери приводят к большой смертности. Дети курящих родителей имеют более низкий вес при рождении, однако маловесящие дети курящих родителей имеют более низкую смертность, чем другие маловесящие дети.
• Парадокс пропавшего доллара (англ.): неправильная логика приводит к тому, что один доллар «пропадает».
• Парадокс корреляции: вполне возможно сделать ложные заключения из корреляции. К примеру, города с бо́льшим количеством церквей имеют больше преступлений, потому что оба фактора следуют из бо́льшего населения. Это называется ложной корреляцией.
• Триада отрицательных корреляций в парадоксе голосования (Парадокс Кондорсе/Arrow’s paradox (англ.)): избиратель 1 ранжирует троих кандидатов в порядке А, В, С; избиратель 2 — в порядке В, С, А; избиратель 3 — в порядке С, А, В. Таким образом, любые две трети избирателей согласны между собой в сравнительной оценке двух третей кандидатов. Но коэффициент ранговой корреляции Спирмена между предпочтениями любых двух избирателей из этой тройки отрицателен и равен −0,5. Отрицательные же корреляции между рангами предпочтений у разных людей характеризуют, по смыслу понятия корреляции, скорее несогласие между этими людьми, чем их согласие.
• Феномен Уилла Роджерса: математическое понятие среднего, определённое как среднее арифметическое или медиана (неважно), приводит к парадоксальному результату — например, возможно переместить статью из Википедии в Викицитатник так, чтобы средняя длина статьи увеличилась на обоих сайтах!
• Парадокс маляра: бесконечную по площади пластинку можно окрасить конечным количеством краски.
• Парадокс Паррондо: возможно выиграть, играя поочерёдно в две заведомо проигрышные игры.
• Парадокс ряда 1−1+1−… (Ряд Гранди): имеется бесконечный ряд 1−1+1−… Чему он равен? Можно доказать, что он равен 0, 1 или 0,5.
• Как ни парадоксально, но при довольно естественных определениях можно показать, что 1 + 2 + 3 + 4 + … = −1/12 (англ.).

Вероятностные

См. также: Категория:Вероятностные парадоксы

• Парадокс Берксона: два независимых события становятся условно зависимыми при условии, что хотя бы одно из них произошло.
• Парадокс Бертрана: различные определения случайной величины, основанные на «здравом смысле», дают различные результаты.
• Парадокс дней рождения: какая вероятность того, что у двух учеников из одного класса день рождения совпадает? Оказывается — более 50 %, если учеников больше 23.

Загадка Монти Холла: в поисках автомобиля игрок выбирает дверь 1. Тогда ведущий открывает третью дверь, за которой находится коза, и предлагает игроку изменить свой выбор на дверь 2. Увеличиваются ли шансы игрока при выборе двери 2?

• Парадокс Бореля (англ.): плотность условной вероятности не инвариантна при преобразованиях координат.
• Пол второго ребенка: если один из двух детей в семье — мальчик, какова вероятность того, что второй ребёнок — девочка?
• Парадокс Монти Холла: неочевидное следствие условной вероятности. По сути дела то же, что и задача трёх узников.
• Парадокс Симпсона: основные интересы подобщества могут оказаться совсем не основными во всём обществе. Поэтому если два ряда данных соответствуют одной определённой гипотезе, будучи объединёнными, они могут соответствовать противоположной гипотезе.
• Задача спящей красавицы: Вероятностная задача, которая может иметь в качестве ответа 1/2 или 1/3 в зависимости от того, с какой стороны рассматривать вопрос.
• Задача трёх карточек (англ.): истинная вероятность того, что обратная сторона случайно выбранной карты окажется того же цвета, что и верхняя, противоречит интуитивной оценке такой вероятности некоторыми людьми.
• Парадокс двух конвертов: вам дают два одинаковых конверта и говорят, что один из них содержит в два раза больше денег, чем другой. Вы должны открыть один из них, проверить содержимое, а затем, не открывая другой, решить, какой из конвертов взять.
• Парадокс пари: в некоторых ситуациях выгодно спорить обоим противникам, ибо оба имеют бо́льшие шансы на победу, чем на проигрыш.
• Парадокс Ходжсона (англ.): отношение двух распределённых гауссово случайных переменных не имеет ни математического ожидания, ни дисперсии
• Ошибка игрока (gambler’s fallacy) — (ложный вывод Монте-Карло) о том, что выгодно ставить на красное, если чёрное выпало 10 раз подряд.
• Санкт-Петербургский парадокс: люди вряд ли будут играть в эту игру, хотя математическое ожидание выигрыша в ней бесконечно велико.
• Парадокс закономерности: увидев явную закономерность в результатах серии испытаний (например, выпадение 10 000 раз подряд одного и того же варианта из двух возможных), мы будем склонны считать, что испытания не являются случайными. Однако появление любой другой последовательности из 10 000 значений в случайных испытаниях является настолько же маловероятным событием.

Связанные с бесконечностью

Геометрические или топологические

• Парадокс Банаха — Тарского: возможно разрезать шар на 5 частей, сложить их по-другому и получится два шара такого же радиуса, как и первоначальный.
• Квадратура круга Тарского‎: круг и квадрат равной площади равносоставлены при конечном разбиении.
• Рог Гавриила (англ.) или «труба Торричелли»: простое тело, имеющее конечный объём, но бесконечную площадь поверхности. Множество Мандельброта и различные другие фракталы имеют конечную площадь, но бесконечный периметр. Более того на границе множества Мандельброта не существует двух различных точек, между которыми конечное расстояние по периметру, что можно понять так: если Вы пойдёте вдоль границы этого множества, Вы нисколько не сдвинетесь из одной точки.
• Парадокс Хаусдорфа: существует счётное подмножество C на сфере S такое, что S\C можно разбить на две копии самого себя.
• Парадокс побережья (англ.): периметр континента не может быть корректно определён (не может быть сопоставлен конкретному числу)

Парадокс Смейла утверждает, что можно вывернуть (с самопересечениями, но без складок) сферу в трёхмерном пространстве. Одна из промежуточных конфигураций, Поверхность Морина (англ.), видна на рисунке.

• Парадокс Смейла: сфера топологически может быть вывернута наизнанку.
• Исчезновение клетки: при различных вариантах складывания одних и тех же элементов в одинаковую фигуру «исчезновение» элемента наглядно демонстрирует, что площади получаемых фигур различны. (При более внимательном рассмотрении, однако, можно заметить, что исходная и конечная фигуры различны, этим и объясняется разница площадей, поэтому данный парадокс относится к визуальным иллюзиям.)

Связанные с выбором

• Парадокс Абилина: бывает, что люди принимают решения, основанные не на том, что они сами хотят, но на том, что они думают, что другие хотят. В результате получается, что каждый делает что-то, что никому на самом деле не нужно.
• Буриданов осёл: как можно совершить рациональный выбор между двумя вещами, имеющими одинаковую ценность?
• Парадокс контроля (англ.): человек не может быть свободен от контроля, ибо чтобы быть свободным от контроля, нужно контролировать себя.
• Вилка Мортона: выбор из двух плохих альтернатив («выбор из двух зол»).
• Загадка Кавки о яде (англ.): может ли человек быть намеренным выпить смертельный яд, если намерение — единственная вещь, которая нужна для получения награды?
• Дилемма заключённого: при некоторых условиях оптимальная стратегия поведения каждого игрока, если каждый игрок исходит из эгоистичных соображений, оказывается проигрышной для группы в целом и для каждого игрока в отдельности.

Химические

Физические

Смотрите статью Парадоксы квантовой механики, Физические парадоксы (англ.).

Из теории относительности и квантовой механики

• Парадокс Белла: разорвётся ли струна, соединяющая релятивистские объекты?
• Парадокс Эйнштейна-Подольского-Розена: могут ли далёкие друг от друга события влиять друг на друга (в квантовой механике)?
• ГЗК-парадокс: наблюдаемые высокоэнергетичные космические лучи, похоже, нарушают предел Грайзена-Зацепина-Кузьмина, который является следствием СТО.
• Парадокс лестницы (англ.): Может ли лестница за счёт релятивистского сокращения длины поместиться в меньший по размеру гараж?
• Кот Шрёдингера. Квантовый парадокс: кот жив или мёртв перед тем, как мы на него посмотрим?
• Парадокс близнецов: когда близнец-путешественник вернулся, он стал моложе или старше, чем его брат, который оставался на Земле?
• Парадокс субмарины: сила Архимеда на релятивистский (англ.) объект (типа пули) изменяется при переходе от системы отсчёта, в которой покоится пуля, в систему отсчёта, в которой покоится жидкость.
• Парадокс Эренфеста о кинематике абсолютно твёрдого вращающегося диска.
• Исчезновение информации в чёрной дыре: чёрная дыра нарушает общепризнанную научную догму — что информация не уничтожается.

Связанные с путешествиями во времени

• Парадокс происхождения (англ.) ставит вопрос о происхождении объектов или информации при путешествиях в прошлое.
• Парадокс убитого дедушки: вы перемещаетесь в прошлое и убиваете своего дедушку до того, как он познакомился с Вашей бабушкой. Из-за этого Вы не сможете появиться на свет и, следовательно, не сможете убить своего дедушку.
• Парадокс предопределения (англ.): человек попадает в прошлое, имеет половую связь со своей прабабушкой и зачинает своего дедушку. В результате получается череда потомков, включая родителя этого человека и его самого. Следовательно, если бы он не путешествовал в прошлое, его бы вообще не существовало.

Гидродинамические

• Парадокс Даламбера: идеальная жидкость не оказывает сопротивления шару, движущемуся в ней.
• Парадокс Архимеда: огромный корабль может плавать в нескольких литрах воды.
• Парадокс чайного листа (англ.): после перемешивания чая чаинки собираются у центра и дна кружки вместо того, чтобы устремляться к ее стенкам под действием центробежной силы.

Термодинамические

• Тепловая смерть вселенной: в 1850 г. немецкий физик Р. Клаузиус «…пришёл к выводу, что в природе теплота переходит от тёплого тела к холодному… состояние Вселенной должно всё больше изменяться в определённом направлении… Эти представления развил английский физик Уильям Томсон, согласно которому все физические процессы во Вселенной сопровождаются превращением световой энергии в теплоту». Следовательно, Вселенную ожидает «тепловая смерть», поэтому бесконечное существование Вселенной во времени невозможно.
• Парадокс теплообмена: две одинаковые массы воды имеют разную температуру. Можно ли путём теплообмена нагреть более холодную воду до более высокой температуры, чем конечная температура охлаждаемой воды? Ведь как известно, тепло может переходить только от более нагретого тела к более холодному.
• Парадокс Гиббса: в идеальном газе является ли энтропия экстенсивной (аддитивной) переменной?
• Парадокс Лошмидта (англ.): почему есть неизбежный рост энтропии, хотя физические законы инвариантны относительно инверсии времени?
• Парадокс перемешивания (англ.) — относительно энтропии системы до и после перемешивания.
• Парадокс Мпембы: горячая вода (при некоторых условиях) может замёрзнуть быстрее, чем холодная. Хотя при этом она должна пройти температуру холодной воды в процессе замерзания.

Другие

• Корпускулярно-волновой дуализм — cвет может рассматриваться либо как электромагнитная волна, скорость распространения в вакууме которой постоянна, либо как поток фотонов — частиц, обладающих определённой энергией, импульсом, собственным моментом импульса и нулевой массой.
• Парадокс Браеса (англ.): устройство, добавляющее мощность сети, может уменьшить общую производительность.
• Парадокс Кэррола (англ.): момент инерции палочки должен быть равен нулю, но он не равен.
• Парадокс Денни: живущие на поверхности воды членистоногие, согласно расчётам, не могут двигаться по поверхности, что противоречит природе.
• Парадокс интернета: вероятность существования нужной информации в Интернете возрастает, а возможность её найти уменьшается.
• Парадокс Ферми: если многие другие разумные существа присутствуют во Вселенной, как это можно предположить, тогда где они? Почему они не дают о себе знать (намеренно или случайно, искусственными излучениями)?
• Фотометрический парадокс (Парадокс звёздного неба, парадокс Шезо — Ольберса): почему ночное небо чёрное, хотя в нём бесконечное число звёзд?
• Ахиллес и черепаха: быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса, так как пока он переместится в точку, где была черепаха, она успеет продвинуться хоть немного вперёд.

Философские

• Тотальная казнь, или парадокс смертной казни: убийство в некоторых странах карается смертной казнью. Но исполняя приговор, государство (то есть все его жители) становятся убийцами и должны быть приговорены к смерти.
• Парадокс эпикурейцев, или Проблема зла: кажется, что существование зла несовместимо с существованием всемогущего и заботливого Бога.
• Парадокс Ньюкома — парадоксы всезнания:
  • Почему можно выиграть у противника, знающего всё?
• Парадокс Хаттона (англ.): если кто-то спрашивает себя: «Сплю ли я?», то это доказывает, что он спит, то что это доказывает во время бодрствования?
• Парадокс либеральности (англ.): «минимальная свобода» не является равновесной по Парето.
• Аддитивность счастья (англ.): что лучше: большая группа людей, живущая сносной жизнью, или небольшая, живущая счастливо?
• Парадокс Мура (англ.): «Идёт дождь, но я не верю в это».
• Парадокс нигилизма (англ.): если правды не существует, то утверждение «правды не существует» верно, что доказывает его неверность.
• Парадокс всемогущества: может ли всемогущее существо создать камень, который оно само не сможет поднять?
• Довольно близок к предыдущему Парадокс непреодолимой силы (англ.): что будет, если непреодолимая сила подействует на несдвигаемый объект? (Оба эти парадокса, после некоторого анализа, могут быть признаны парадоксами противоречивых посылок (англ.), либо в житейском смысле посылки будут уточнены как «непреодолимая ранее сила», воздействуя на «несдвигаемый ранее объект», даст невиданное ранее.)
• Стрела Зенона: летящая стрела каждый момент времени занимает определенное положение в пространстве. Когда же она перемещается из одного положения в другое?
• Дихотомия: «Вы никогда не попадёте из точки А в точку Б, так как вы должны будете пройти половину пути, потом половину оставшейся половины, и так бесконечное число раз».

Экономические

См. также: Category:Economics paradoxes (англ.)

• Парадокс Алле: изменение возможного дохода, который разделён между несколькими альтернативами, влияет на выбор людей между этими альтернативами, что противоречит теории ожидаемой пользы (англ.).
• Парадокс Базермана^[1].
• Парадокс бережливости: если каждый будет экономить деньги во время экономического спада, то совокупный спрос упадёт и в результате уменьшатся суммарные накопления населения.
• Парадокс Бертрана — ситуация, когда два олигополиста, конкурируя между собой и достигнув равновесия Нэша, оказываются с нулевой прибылью.
• Парадокс Гибсона (англ.): почему процентные ставки и цены скоррелированы?
• Парадокс Коперника — Грешема: плохие деньги вытесняют хорошие, если они имеют одинаковую цену.
• Парадокс Гиффена: если цены на хлеб начнут повышаться, люди станут покупать его больше.
• Парадокс Джевонса: повышение эффективности ведёт к ещё бо́льшему повышению спроса.
• Парадокс Кондорсе — парадокс теории общественного выбора: правило простого большинства не в состоянии обеспечить транзитивность бинарного отношения общественного предпочтения среди выбираемых вариантов. В силу нетранзитивности результат может зависеть от порядка голосования, что даёт возможность манипуляции выбором большинства. Обобщён теоремой «о невозможности» Эрроу в 1951 г.
• Парадокс Леонтьева: некоторые страны экспортируют трудозатратные товары, а импортируют капиталозатратные, что является контрпримером к теории Хекшера — Олина.
• Парадокс продуктивности (англ.): продуктивность работника уменьшается, несмотря на улучшения в технологиях.
• Парадокс Триффина: для формирования долларовых резервов других стран необходимо, чтобы в США постоянно наблюдался дефицит платёжного баланса. Но дефицит платёжного баланса подрывает доверие к доллару и снижает его ценность в качестве резервного актива.
• Парадокс ценности: почему вода стоит дешевле алмазов, хотя потребность человека в ней гораздо больше, чем в алмазах?
• Парадокс Эджворта (англ.): может не существовать равновесия, если мощности производств ограничены.
• Парадокс Элсберга (англ.): люди предпочитают известный, хотя и бо́льший, риск неизвестному риску, что противоречит теории ожидаемой пользы (англ.).

Юридические

• Парадокс неподсудного договора: если существует процессуальное правило о том, что судья, рассматривающий дело, не должен быть заинтересован в исходе его рассмотрения, то дело, имеющее в себе договор, содержащий следующее условие: «Каждый судья, который будет рассматривать дело, в котором этот договор является доказательством, в случае признания его ничтожным имеет право получить от каждой из его сторон по 1 копейке», не может быть рассмотрено никаким судьёй^[2].

Психофизиологические

См. также

Примечания

Ссылки

Список парадоксов

Логические (кроме математических)

• Парадокс импликации (англ.): Несовместные посылки делают аргумент верным.
• Парадокс воронов (или Во́роны Хемпеля): Существование красного яблока увеличивает вероятность того, что все во́роны чёрные.
• Доказательство одноцветности всех лошадей методом математической индукции.
• Парадокс неожиданной казни: Если сказать осуждённому на казнь, что она произойдёт в неожиданный для него день этой недели, то он логически придёт к выводу, что она не может произойти ни в один из дней недели. Тогда она и будет сюрпризом. Парадокс сатанинской бутылки Стивенсона(англ.) описывается схожей логикой.
• Парадокс пьяницы (англ.): В любом непустом заведении всегда существует человек такой, что если он пьёт, то пьют и все остальные посетители.
• Парадокс Кэррола (англ.): «Whatever Logic is good enough to tell me is worth writing down…»
• Парадокс лотереи (англ.): Вполне ожидаемо (и философски проверяемо (англ.)), что данный конкретный билет не выиграет, но нельзя ожидать, что никакой билет не выиграет.
Парадоксы самореференции (самоотносимости)
Это хорошо известный (и хорошо изученный) класс противоречий, возникаемых из-за ссылки на само себя.
• Парадокс Берри (англ.): Фраза «наименьшее число, которое нельзя описать менее, чем десятью словами» описывает это число девятью словами.
• Парадокс Карри: «Если это утверждение верно, то русалки существуют»
• Парадокс Эпименида: Критянин говорит: «Все критяне — лжецы»
• Парадокс исключений (англ.): «Если у каждого правила есть исключения, то каждое правило должно иметь хотя бы одно исключение, кроме этого» …а это не исключение к правилу, которое утверждает, что у каждого правила есть исключения?
• Парадокс Греллинга-Нельсона (англ.): Является ли слово «гетерологичный», означающее «неприменимый к самому себе», гетерологичным словом? (Близко к Парадоксу Рассела)
• Парадокс Гегеля: «История учит человека тому, что человек ничему не учится из истории»
• Парадокс лжеца: «Это предложение ложно»
• Y-комбинатор в лямбда-исчислении и комбинаторной логике был назван парадоксальным комбинатором так как он связан с самоотносимостью.
• Парадокс Петрония: «Ограничивайте себя во всех вещах, даже в ограничении»
• Парадокс Квина (англ.): «…влечёт за собой ложность, будучи добавленным к собственному цитированию» влечёт за собой ложность, будучи добавленным к собственному цитированию
• Парадокс Эватла (софизм Эватла): Протагор взял ученика Эватла при условии, что тот ему заплатит, когда выиграет первое дело. Случилось так, что Протагор подал иск на Эватла за то, что тот ему долго не платит. Должен ли Эватл заплатить, если он выиграет это дело (хотя выигрыш означает, что Эватл ничего не должен Протагору)?
• Парадокс Рассела: Содержит ли множество всех таких множеств, которые не содержат себя, самого себя? Рассел популяризовал его в форме парадокса брадобрея: «Брадобрей бреет всех людей, которые не бреются сами. Бреет ли он себя?»
• Парадокс Ришара (англ.): Если сопоставить все свойства чисел с числами, то можно определить такое свойство, которому не будет соответствовать никакое число.
• Прикажите слуге не слушаться Вас. Не слушаясь Вас, он ослушается приказа, так как он исполняет его, не слушаясь Вас.
• Парадокс определения: Невозможно дать определение определению, ибо пока мы не дали это определение, само понятие определения остается неизвестным.
 Парадоксы определений
• Корабль Тесея Если каждый элемент корабля был заменён хотя бы один раз, можно ли считать корабль прежним кораблём?
• Парадокс кучи (англ.): В какой момент куча перестанет быть кучей, если отнимать от неё по одной песчинке? Или, в какой конкретно день какой-либо человек становится лысым?
• Парадокс лысого
• Парадокс интересных чисел (англ.). Первое неинтересное число интересно само по себе этим фактом. Поэтому неинтересных чисел не существует.
Математические и статистические
 
 
Математические парадоксы
• Парадоксы пропорционального представительства в США (en): Некоторые системы представительства могут иметь последствия, идущие против интуиции: 
o Парадокс Алабамы
o Парадокс новых штатов
o Парадокс населения(англ.)
• Парадокс голосования (Парадокс Кондорсе/Arrow’s paradox(англ.)) Нельзя совместить все требования к избирательной системе в одной системе.
• Закон Бенфорда (англ.): Во многих списках чисел из произвольных реальных источников, большинство чисел начинаются с цифры 1.
• Парадокс лифта (англ.): Лифты чаще всего ходят в одном направлении — от середины здания вниз к подвалу и вверх к чердаку
• Парадокс ожидания: Почему иногда приходится ждать автобус дольше, чем нужно. (пояснение смотрите в англ. статье Renewal theory)
• Игра в нетранзитивные кости (англ.): существует набор из 3 костей А, В и С таких, что чаще всего на А выпадает бо́льшее число, чем на В; на В чаще выпадает бо́льшее число, чем на С; на С чаще выпадает бо́льшее число, чем на А.
• Парадокс Линдли (англ.): маленькие ошибки в нулевой гипотезе сильно возрастают, если анализируются большие массивы данных, приводя к ложным, но одновременно точным со статистической точки зрения результатам.
• Парадокс недоношенности (англ.): Низкий вес при рождении и курение матери приводят к большой смертности. Дети курящих родителей имеют более низкий вес при рождении, однако маловесящие дети курящих родителей имеют более низкую смертность, чем другие маловесящие дети.
• Парадокс пропавшего доллара (англ.): Неправильная логика приводит к тому, что один доллар «пропадает».
• Парадокс корреляции: Вполне возможно сделать ложные заключения из корреляции. К примеру, города с бо́льшим количеством церквей имеют больше преступлений, потому что оба фактора следуют из бо́льшего населения. Это называется ложной корреляцией.
• Феномен Уилла Роджерса: математическое понятие среднего, определённое как среднее арифметическое, или как медиана — неважно, приводит к парадоксальному результату — например, возможно переместить статью из Википедия в Викицитатник так, чтобы средняя длина статьи увеличилась на обоих сайтах!
• Парадокс Райта (англ.): Ребёнок стареет быстрее, чем старик, так как удвоение возраста — более частое явление в начале процесса, чем в конце.
• Парадокс маляра: Бесконечную по площади пластинку можно окрасить конечным количеством краски.
Вероятностные

• Парадокс Берксона: два независимых события становятся условно зависимыми при условии, что хотя бы одно из них произошло.
• Парадокс Бертрана (теория вероятности) (англ.): Различные определения случайной величины, основанные на «здравом смысле», дают различные результаты.
• Парадокс дней рождения : Какая вероятность того, что у двоих учеников из одного класса день рождения совпадает? Оказывается — больше половины, если учеников больше 23 !
• Парадокс Бореля (англ.): Плотность условной вероятности не инвариантна при преобразованиях координат.
• Пол второго ребёнка (парадокс) (англ.): Если один из двух детей в семье — мальчик, какова вероятность того, что второй ребёнок — девочка?
• Парадокс Монти Холла: Неочевидное следствие условной вероятности. По сути дела то же, что и задача трёх узников (англ.).
• Парадокс Симпсона: Основные интересы подобщества могут оказаться совсем не основными во всём обществе. Поэтому если два ряда данных соответствуют одной определённой гипотезе, будучи объединёнными, они могут соответствовать противоположной гипотезе.
• Задача спящей красавицы (англ.): Вероятностная задача, которая может иметь в качестве ответа 1/2 или 1/3 в зависимости от того, с какой стороны рассматривать вопрос.
• Задача трёх карточек (англ.): Истинная вероятность того, что обратная сторона случайно выбранной карты окажется того же цвета, что и верхняя, противоречит интуитивной оценке такой вероятности некоторыми людьми.
• Парадокс двух конвертов (англ.): Вам дают два одинаковых конверта и говорят, что один из них содержит в два раза больше денег, чем другой. Вы должны открыть один из них, проверить содержимое, а затем, не открывая другой, решить, какой из конвертов взять.
• Парадокс пари (англ.). В некоторых ситуациях выгодно спорить обоим противникам, ибо оба имеют бо́льшие шансы на победу, чем на проигрыш.
• Парадокс Ходжсона (англ.): Отношение двух распределённых гауссово случайных переменных не имеет ни математического ожидания, ни дисперсии
Ошибка игрока (gambler’s fallacy) — (ложный вывод Монте-Карло) о том, что выгодно ставить на красное, если чёрное выпало 10 раз подряд.
• Санкт-Петербургский парадокс: Люди вряд ли будут играть в эту игру, хотя математическое ожидание выигрыша в ней бесконечно велико.
Связанные с бесконечностью
• Парадокс Бурали-Форти: Если бы все порядковые числа (в том числе и трансфинитные) образовывали множество, тогда существовало бы порядковое число, которое меньше самого себя.
• Парадокс Галилея: Хотя большинство чисел не является квадратами, всех натуральных чисел не больше, чем квадратов (если сравнивать эти множества по мощности). (См. также Г. Кантор, Diagonal Argument(англ.))
• Парадокс Гильберта (англ.): Если гостиница с бесконечным количеством номеров полностью заполнена, в неё можно поселить ещё посетителей, даже бесконечное число.
• Парадокс Дьявольского Монти (англ.): Положительная прибыль каждый день приводит к нулевому балансу в (бесконечном) пределе.
• Парадокс Сколема: Счётное количество бесконечных моделей теории множеств содержит несчётные множества.
• Многие бесконечные задачи (англ.) приводят к парадоксам, например, задача об апельсинах (англ.).
Геометрические или топологические
 
 
Парадокс Банаха — Тарского: Шар может быть разложен на несколько частей, из которых потом можно сложить два точно таких же шара.
• Парадокс Банаха — Тарского: Возможно разрезать шар на 5 частей, сложить их по-другому и получится два шара такого же радиуса, как и первоначальный.
• Рог Гавриила (англ.) или «труба Торричелли»: Простое тело, имеющее конечный объём, но бесконечную площадь поверхности. Множество Мандельброта и различные другие фракталы имеют конечную площадь, но бесконечный периметр. Более того на границе множества Мандельброта не существует двух различных точек, между которыми конечное расстояние по периметру, что можно понять так: если Вы пойдёте вдоль границы этого множества, Вы нисколько не сдвинетесь из одной точки.
• Парадокс Хаусдорфа: Существует счётное подмножество C на сфере S такое, что SC можно разбить на две копии самого себя.
• Парадокс побережья (англ.): периметр континента не может быть корректно определён (не может быть сопоставлен конкретному числу)
 
 
Парадокс Смейла утверждает, что можно вывернуть (с самопересечениями, но без складок) сферу в 3-мерном пространстве. 
• Парадокс Смейла: Сфера, топологически, может быть вывернута наизнанку.
• Головоломка с пропаданием квадрата: Две похожие фигуры имеют различные площади, хотя составлены из одинаковых элементов.
Связанные с выбором

• Парадокс Абилина: Бывает, что люди принимают решения, основанные не на том, что они сами хотят, но на том, что они думают, что другие хотят. В результате получается, что каждый делает что-то, что никому на самом деле не нужно.
• Буриданов осёл: Как можно совершить рациональный выбор между двумя вещами, имеющими одинаковую ценность?
• Парадокс контроля (англ.): Человек не может быть свободен от контроля, ибо чтобы быть свободным от контроля, нужно контролировать себя.
• Вилка Мортона: Выбор из двух плохих альтернатив («выбор из двух зол»).
• Загадка Кавки о яде (англ.): Может ли человек быть намеренным выпить смертельный яд, если намерение — единственная вещь, которая нужна для получения награды?
• Дилемма заключённого: При некоторых условиях оптимальная стратегия поведения каждого игрока, если каждый игрок исходит из эгоистичных соображений, оказывается проигрышной для группы в целом и для каждого игрока в отдельности.
 Химические
• SAR-парадокс (англ.): Исключения из правила, что малое изменение в молекуле влечёт за собой малое изменение в химическом поведении, часто очень глубоки по смыслу.
• Парадокс Левинталя (англ.): Промежуток времени, за который протеиновая цепочка приходит к своему скрученному состоянию, на много порядков меньше, чем оно могло бы быть, если она просто перебирала все возможные конфигурации.
Физические

Из теории относительности и квантовой механики
• Парадокс Архимеда (англ.). Огромный корабль может плавать в нескольких литрах воды.
• Парадокс Белла: Разорвётся ли струна, соединяющая релятивистские объекты?
• Парадокс Эйнштейна-Подольского-Розена: Могут ли далёкие друг от друга события влиять друг на друга (в квантовой механике)?
• ГЗК-парадокс (англ.): Наблюдаемые высокоэнергетичные космические лучи, похоже, нарушают предел Грайзена-Зацепина-Кузьмина, который является следствием СТО.
• Парадокс лестницы (англ.): Может ли лестница за счёт релятивистского сокращения длины поместиться в меньший по размеру гараж?
• Кот Шрёдингера. Квантовый парадокс: кот жив или мёртв перед тем, как мы на него посмотрим?
• Парадокс близнецов: Когда близнец-путешественник вернулся, он стал моложе или старше, чем его брат, который оставался на Земле?
• Парадокс субмарины: Сила Архимеда на релятивистский (англ.) объект (типа пули) изменяется при переходе от системы отсчёта, в которой покоится пуля, в систему отсчёта, в которой покоится жидкость.
• Парадокс Эренфеста о кинематике абсолютно твёрдого вращающегося диска.
• Информационный парадокс
Связанные с путешествиями во времени
• Парадокс происхождения (англ.) ставит вопрос о происхождении объектов или информации при путешествиях в прошлое.
• Парадокс дедушки (англ.): Вы перемещаетесь в прошлое и убиваете своего дедушку до того, как он познакомился с Вашей бабушкой. Из-за этого Вы не сможете появиться на свет и, следовательно, не сможете убить своего дедушку.
• Парадокс предопределения (англ.): Человек попадает в прошлое, имеет половую связь со своей прабабушкой и зачинает своего дедушку. В результате получается череда потомков, включая родителя этого человека и его самого. Следовательно, если бы он не путешествовал в прошлое, его бы вообще не существовало.
Гидродинамические
• Парадокс Даламбера (англ.): Идеальная жидкость не оказывает сопротивления шару, движущемуся в ней.
Другие
• Исчезновение информации в чёрной дыре: Чёрная дыра нарушает общепризнанную научную догму — что информация не уничтожается.
• Парадокс Браеса (англ.): Устройство, добавляющее мощность сети, может уменьшить общую производительность.
• Парадокс Кэррола (англ.): Момент инерции палочки должен быть равен нулю, но он не равен.
• Парадокс Денни: Живущие на поверхности воды членистоногие, согласно расчётам, не могут двигаться по поверхности, что противоречит природе.
• Парадокс интернета: Вероятность существования нужной информации в Интернете возрастает, а возможность её найти уменьшается.
• Парадокс Ферми: Если многие другие разумные существа присутствуют во Вселенной, как это можно предположить, тогда где они? Почему они не дают о себе знать (намеренно или случайно, искусственными излучениями)?
• Парадокс Гиббса: В идеальном газе является ли энтропия экстенсивной (аддитивной) переменной?
• Парадокс Лошмидта (англ.): Почему есть неизбежный рост энтропии, хотя физические законы инвариантны относительно инверсии времени?
• Парадокс перемешивания (англ.) — относительно энтропии системы до и после перемешивания.
• Парадокс Мпембы (англ.): Горячая вода (при некоторых условиях) может замёрзнуть быстрее, чем холодная. Хотя при этом она должна пройти температуру холодной воды в процессе замерзания.
• Фотометрический парадокс: Почему ночное небо — чёрное, хотя в нём бесконечное число звёзд?
 Философские
• Тотальная казнь, или парадокс смертной казни: Убийство в некоторых странах карается смертной казнью. Но совершая её, государство (то есть все его жители) становятся убийцами и должны быть приговорены к смерти.
• Парадокс эпикурейцев, или Проблема зла (англ.): Кажется, что существование зла несовместимо с существованием всемогущего и заботливого Бога.
• Парадокс Ньюкома — парадоксы всезнания: 
o Если существует знающее всё существо (Бог), то невозможно иметь свободную волю, так как это существо будет знать, что вы хотите предпринять, а значит вы не можете принять решение, потому что оно уже сделано до вас.
o Почему можно выиграть у противника, знающего всё?
• Парадокс Хаттона (англ.): Если кто-то спрашивает себя «Сплю ли я?», то это доказывает, что он спит, то что это доказывает во время бодрствования?
• Парадокс либеральности (англ.): «Минимальная свобода» не является равновесной по Парето.
• Аддитивность счастья (англ.): Что лучше: большая группа людей, живущая сносной жизнью, или небольшая, живущая счастливо?
• Парадокс Мура (англ.): «Идёт дождь, но я не верю в это»
• Парадокс нигилизма (англ.): Если правда не существует, то утверждение «правда не существует» верно, что доказывает его неверность.
• Парадокс всемогущества: Может ли всемогущее существо создать камень, который оно само не сможет поднять?
• Довольно близок к предыдущему Парадокс непреодолимой силы (англ.): Что будет, если непреодолимая сила подействует на несдвигаемый объект? (Оба эти парадокса, после некоторого анализа, могут быть признаны парадоксами противоречивых посылок (англ.))
• Парадокс гедонизма: Когда человек занимается только своим счастьем, он несчастен; но, занимаясь другими вещами, он может быть счастливым.
• Стрела Зенона: Летящая стрела каждый момент времени занимает определенное положение в пространстве. Когда же она перемещается из одного положения в другое?
• Дихотомия: «Вы никогда не попадёте из точки А в точку Б, так как вы должны будете пройти половину пути, потом половину оставшейся половины, и так бесконечное число раз»
Экономические
См. также: Category:Economics paradoxes(англ.)
• Парадокс Бертрана — ситуация, когда два олигополиста, конкурируя между собой и достигнув равновесия Нэша, оказываются с нулевой прибылью.
• Парадокс Аллэ: Изменение возможного дохода, который разделён между несколькими альтернативами, влияет на выбор людей между этими альтернативами, что противоречит теории ожидаемой пользы (англ.).
• Парадокс ценности: Почему вода стоит дешевле алмазов, хотя потребность человека в ней гораздо больше, чем в алмазах?
• Парадокс Эджворта (англ.): Может не существовать равновесия, если мощности производств ограничены.
• Парадокс Элсберга (англ.): Люди предпочитают известный, хотя и бо́льший, риск неизвестному риску, что противоречит теории ожидаемой пользы (англ.).
• Парадокс Гибсона (англ.): Почему процентные ставки и цены скоррелированы?
• Парадокс Гиффена: Если цены на хлеб начнут повышаться, люди станут покупать его больше.
• Парадокс Джевонса (англ.): Повышение эффективности ведёт к ещё бо́льшему повышению спроса.
• Парадокс Леонтьева: Некоторые страны экспортируют трудозатратные товары, а импортируют капиталозатратные, что является контрпримером к теории Хекшера — Олина.
• Парадокс бережливости: Если каждый будет экономить деньги во время экономического спада, то совокупный спрос упадёт и в результате уменьшатся суммарные накопления населения.
• Парадокс Паррондо (англ.): Возможно выиграть, играя поочерёдно в две заведомо проигрышные игры.
• Парадокс продуктивности (англ.): Продуктивность работника уменьшается, несмотря на улучшения в технологиях

Циклопедия:Списки:Парадоксы — Циклопедия

Это список парадоксов, сгруппированных по темам.

Парадокс Левинталя [Диалоги Гордона]

Парадо́кс (от др.-греч. παράδοξος — неожиданный, странный; от παρα-δοκέω — кажусь) — ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения. Следует различать парадокс и апорию: последняя, в отличие от парадокса, является вымышленной, логически верной ситуацией (высказыванием, утверждением, суждением или выводом), которая не может существовать в реальности.

[править] Логические (кроме математических)

 → Логика

[править] Парадоксы самореференции (самоотносимости)

Это хорошо известный (и хорошо изученный) класс противоречий, возникающих в высказываниях, которые содержат определение чего-либо, неявно ссылающееся на само себя.

• Парадокс Берри: фраза — «наименьшее число, которое нельзя описать менее, чем десятью словами» — описывает это число девятью словами.
• Парадокс Карри: «Если это утверждение верно, то русалки существуют».
• Парадокс крокодила: Крокодил украл ребёнка и обещал матери отдать его, если она верно ответит, отдаст ли крокодил ей ребёнка.
• Парадокс Эпименида: критянин говорит: «Все критяне — лжецы».
• Парадокс исключений: «Если у каждого правила есть исключения, то каждое правило должно иметь хотя бы одно исключение, кроме этого» … а это не исключение к правилу, которое утверждает, что у каждого правила есть исключения?
• Парадокс Греллинга-Нельсона: является ли слово «гетерологичный», означающее «неприменимый к самому себе», гетерологичным словом? (Близко к Парадоксу Рассела.)
• Парадокс Гегеля: «История учит человека тому, что человек ничему не учится из истории».
• Y-комбинатор в лямбда-исчислении и комбинаторной логике был назван парадоксальным комбинатором так как он связан с самоотносимостью.
• Парадокс Петрония: «Ограничивайте себя во всех вещах, даже в ограничении».
• Парадокс Квина: «… влечёт за собой ложность, будучи добавленным к собственному цитированию» влечёт за собой ложность, будучи добавленным к собственному цитированию.
• «Парадокс Эватла» (софизм Эватла): Протагор взял ученика Эватла при условии, что тот ему заплатит, когда выиграет первое дело. Случилось так, что Протагор подал иск на Эватла за то, что тот ему долго не платит. Должен ли Эватл заплатить, если он выиграет это дело?
• Парадокс Рассела: содержит ли множество всех множеств, которые не содержат себя, само себя? Рассел популяризовал его в форме «парадокса брадобрея»: «Брадобрей бреет только тех людей, которые не бреются сами. Бреет ли он себя?»
• Парадокс Ришара: если сопоставить все свойства чисел с числами, то можно определить такое свойство, которому не будет соответствовать никакое число.
• Парадокс всемогущества: может ли всемогущее существо создать камень, который оно само не сможет поднять?

[править] Парадоксы определений

• Корабль Тесея: если каждый элемент корабля был заменён хотя бы один раз, можно ли считать корабль прежним кораблём?
• Парадокс кучи. В какой момент куча перестанет быть кучей, если отнимать от неё по одной песчинке?
• Парадокс лысого: если волосы с головы выпадают по одному, с какого момента человек становится лысым?
• Парадокс интересных чисел: наименьшее неинтересное натуральное число интересно само по себе этим фактом, но тогда оно не относится к неинтересным.

[править] Математические и статистические

 → Математика

См. также: Категория:Математические парадоксы

• Парадоксы пропорционального представительства в США (en): некоторые системы представительства могут иметь последствия, идущие против интуиции:
• Парадокс голосования (Парадокс Эрроу): нельзя совместить все требования к избирательной системе в одной системе.
• Закон Бенфорда: во многих списках чисел из произвольных реальных источников большинство чисел начинаются с цифры 1.
• Парадокс лифта: лифты чаще всего ходят в одном направлении — от середины здания вниз к подвалу и вверх к чердаку
• Парадокс ожидания: почему иногда приходится ждать автобус дольше, чем нужно. (пояснение смотрите в англ. статье Renewal theory)
• Игра в нетранзитивные кости: существует набор из 3 костей А, В и С таких, что чаще всего на А выпадает бо́льшее число, чем на В; на В чаще выпадает бо́льшее число, чем на С; на С чаще выпадает бо́льшее число, чем на А.
• Игра Пенни: нетранзитивный парадокс, разновидность игры в нетранзитивные кости.
• Парадокс Линдли (англ.): маленькие ошибки в нулевой гипотезе сильно возрастают, если анализируются большие массивы данных, приводя к ложным, но одновременно точным со статистической точки зрения результатам.
• Парадокс недоношенности (англ.): низкий вес при рождении и курение матери приводят к большой смертности. Дети курящих родителей имеют более низкий вес при рождении, однако маловесящие дети курящих родителей имеют более низкую смертность, чем другие маловесящие дети.
• Парадокс пропавшего доллара (англ.): неправильная логика приводит к тому, что один доллар «пропадает».
• Парадокс корреляции: вполне возможно сделать ложные заключения из корреляции. К примеру, города с бо́льшим количеством церквей имеют больше преступлений, потому что оба фактора следуют из бо́льшего населения. Это называется ложной корреляцией.
• Триада отрицательных корреляций в парадоксе голосования (Парадокс Кондорсе/Arrow’s paradox(англ.)): избиратель 1 ранжирует троих кандидатов в порядке А, В, С; избиратель 2 — в порядке В, С, А; избиратель 3 — в порядке С, А, В. Таким образом, любые две трети избирателей согласны между собой в сравнительной оценке двух третей кандидатов. Но коэффициент ранговой корреляции Спирмена между предпочтениями любых двух избирателей из этой тройки отрицателен и равен −0,5. Отрицательные же корреляции между рангами предпочтений у разных людей характеризуют, по смыслу понятия корреляции, скорее несогласие между этими людьми, чем их согласие.
• Феномен Уилла Роджерса: математическое понятие среднего, определённое как среднее арифметическое или медиана (неважно), приводит к парадоксальному результату — например, возможно переместить статью из Википедии в Викицитатник так, чтобы средняя длина статьи увеличилась на обоих сайтах!
• Парадокс маляра: бесконечную по площади пластинку можно окрасить конечным количеством краски.
• Парадокс Паррондо: возможно выиграть, играя поочерёдно в две заведомо проигрышные игры.
• Парадокс ряда 1−1+1−… (Ряд Гранди): имеется бесконечный ряд 1−1+1−… Какова его сумма? Можно доказать, что она равна 0, 1 или 0,5.
• Существует несколько доказательств, что сумма всех натуральных чисел 1 + 2 + 3 + 4 + … = −¹⁄₁₂.

[править] Вероятностные

 → Теория вероятностей

См. также: Категория:Вероятностные парадоксы

• Парадокс Берксона: два независимых события становятся условно зависимыми при условии, что хотя бы одно из них произошло.
• Парадокс Бертрана: различные определения случайной величины, основанные на «здравом смысле», дают различные результаты.
• Парадокс дней рождения: какая вероятность того, что у двух учеников из одного класса день рождения совпадает? Оказывается — более 50 %, если учеников больше 23.

Загадка Монти Холла: в поисках автомобиля игрок выбирает дверь 1. Тогда ведущий открывает третью дверь, за которой находится коза, и предлагает игроку изменить свой выбор на дверь 2. Увеличиваются ли шансы игрока при выборе двери 2?

• Парадокс Бореля (англ.): плотность условной вероятности не инвариантна при преобразованиях координат.
• Пол второго ребёнка: если один из двух детей в семье — мальчик, какова вероятность того, что второй ребёнок — девочка?
• Парадокс Монти Холла: неочевидное следствие условной вероятности. По сути дела то же, что и задача трёх узников.
• Парадокс Симпсона: основные интересы подобщества могут оказаться совсем не основными во всём обществе. Поэтому если два ряда данных соответствуют одной определённой гипотезе, будучи объединёнными, они могут соответствовать противоположной гипотезе.
• Задача спящей красавицы: Вероятностная задача, которая может иметь в качестве ответа 1/2 или 1/3 в зависимости от того, с какой стороны рассматривать вопрос.
• Задача трёх карточек: истинная вероятность того, что обратная сторона случайно выбранной карты окажется того же цвета, что и верхняя, противоречит интуитивной оценке такой вероятности некоторыми людьми.
• Парадокс двух конвертов: вам дают два одинаковых конверта и говорят, что один из них содержит в два раза больше денег, чем другой. Вы должны открыть один из них, проверить содержимое, а затем, не открывая другой, решить, какой из конвертов взять.
• Парадокс пари: в некоторых ситуациях выгодно спорить обоим противникам, ибо оба имеют бо́льшие шансы на победу, чем на проигрыш.
• Парадокс Ходжсона (англ.): отношение двух распределённых гауссово случайных переменных не имеет ни математического ожидания, ни дисперсии
• Ошибка игрока (gambler’s fallacy) — (ложный вывод Монте-Карло) о том, что выгодно ставить на красное, если чёрное выпало 10 раз подряд.
• Санкт-Петербургский парадокс: люди вряд ли будут играть в эту игру, хотя математическое ожидание выигрыша в ней бесконечно велико.
• Парадокс закономерности: увидев явную закономерность в результатах серии испытаний (например, выпадение 10 000 раз подряд одного и того же варианта из двух возможных), мы будем склонны считать, что испытания не являются случайными. Однако появление любой другой последовательности из 10 000 значений в случайных испытаниях является настолько же маловероятным событием.

[править] Связанные с бесконечностью

[править] Геометрические или топологические

• Парадокс Банаха — Тарского: возможно разрезать шар на 5 частей, сложить их по-другому и получится два шара такого же радиуса, как и первоначальный.
• Квадратура круга Тарского: круг и квадрат равной площади равносоставлены при конечном разбиении.
• Рог Гавриила (англ.) или «труба Торричелли»: простое тело, имеющее конечный объём, но бесконечную площадь поверхности. Множество Мандельброта и различные другие фракталы имеют конечную площадь, но бесконечный периметр. Более того на границе множества Мандельброта не существует двух различных точек, между которыми конечное расстояние по периметру, что можно понять так: если Вы пойдёте вдоль границы этого множества, Вы нисколько не сдвинетесь из одной точки.
• Парадокс Хаусдорфа: существует счётное подмножество C на сфере S такое, что S\C можно разбить на две копии самого себя.
• Парадокс побережья (англ.): периметр континента не может быть корректно определён (не может быть сопоставлен конкретному числу)

Парадокс Смейла утверждает, что можно вывернуть (с самопересечениями, но без складок) сферу в трёхмерном пространстве. Одна из промежуточных конфигураций, Поверхность Морина (англ.), видна на рисунке.

• Парадокс Смейла: сфера топологически может быть вывернута наизнанку.
• Исчезновение клетки: при различных вариантах складывания одних и тех же элементов в одинаковую фигуру «исчезновение» элемента наглядно демонстрирует, что площади получаемых фигур различны. (Правда, можно заметить, что исходная и конечная фигуры различны — гипотенуза треугольников является не прямой линией, а разными ломанными. Этим и объясняется разница площадей, поэтому данный парадокс относится к визуальным иллюзиям.)

[править] Связанные с выбором

 → Теория принятия решений

• Парадокс Абилина: бывает, что люди принимают решения, основанные не на том, что они сами хотят, но на том, что они думают, что другие хотят. В результате получается, что каждый делает что-то, что никому на самом деле не нужно.
• Буриданов осёл: как можно совершить рациональный выбор между двумя вещами, имеющими одинаковую ценность?
• Парадокс контроля (англ.): человек не может быть свободен от контроля, ибо чтобы быть свободным от контроля, нужно контролировать себя.
• Вилка Мортона: выбор из двух плохих альтернатив («выбор из двух зол»).
• Загадка Кавки о яде (англ.): может ли человек быть намеренным выпить несмертельный яд, если намерение — единственная вещь, которая нужна для получения награды?
• Дилемма заключённого: при некоторых условиях оптимальная стратегия поведения каждого игрока, если каждый игрок исходит из эгоистичных соображений, оказывается проигрышной для группы в целом и для каждого игрока в отдельности.

Смотрите статью Парадоксы квантовой механики, Физические парадоксы (англ.).

[править] Из теории относительности и квантовой механики

• Парадокс Белла: разорвётся ли струна, соединяющая релятивистские объекты?
• Парадокс Эйнштейна-Подольского-Розена: могут ли далёкие друг от друга события влиять друг на друга (в квантовой механике)?
• ГЗК-парадокс: наблюдаемые высокоэнергетичные космические лучи, похоже, нарушают предел Грайзена-Зацепина-Кузьмина, который является следствием СТО.
• Парадокс шеста и сарая (Парадокс лестницы): Может ли шест за счёт релятивистского сокращения длины поместиться в меньший по размеру сарай?
• Кот Шрёдингера. Квантовый парадокс: кот жив или мёртв перед тем, как мы на него посмотрим? Связанный с ним парадокс друга Вигнера.
• Парадокс близнецов: когда близнец-путешественник вернулся, он стал моложе или старше, чем его брат, который оставался на Земле?
• Парадокс субмарины: сила Архимеда на релятивистский (англ.) объект (типа пули) изменяется при переходе от системы отсчёта, в которой покоится пуля, в систему отсчёта, в которой покоится жидкость.
• Парадокс Эренфеста о кинематике абсолютно твёрдого вращающегося диска.
• Исчезновение информации в чёрной дыре: чёрная дыра нарушает общепризнанную научную догму — что информация не уничтожается.

[править] Необычные явления, мысленные эксперименты и парадоксы квантовой механики

• Соотношение неопределённостей Гейзенберга. Соотношение неопределённости возникает между любыми квантовыми наблюдаемыми, определяемыми некоммутирующими операторами. Согласно соотношению неопределённостей, невозможно абсолютно точно определить одновременно координаты и импульс частицы. С повышением точности измерения координаты, максимальная точность измерения импульса уменьшается и наоборот.
• Корпускулярно-волновой дуализм — принцип, согласно которому любой физический объект может быть описан как с использованием математического аппарата, основанного на волновых уравнениях, так и с помощью формализма, основанного на представлении об объекте как о частице или как о системе частиц. В частности, волновое уравнение Шрёдингера не накладывает ограничений на массу описываемых им частиц, и следовательно, любой частице, как микро-, так и макро-, может быть поставлена в соответствие волна де Бройля.
• Дифракция электронов — процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет волновые свойства. Данное явление объясняется корпускулярно-волновым дуализмом, в том смысле, что частица вещества (в данном случае взаимодействующий с веществом электрон) может быть описана, как волна.
• Сверхтекучесть (Бозе-конденсат) — способность вещества в особом состоянии (квантовой жидкости), возникающем при понижении температуры к абсолютному нулю (термодинамическая фаза), протекать через узкие щели и капилляры без трения.
• Сверхпроводимость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура).
• Квантовая телепортация — передача квантового состояния на расстояние при помощи разъединённой в пространстве сцепленной (запутанной) пары и классического канала связи, при которой состояние разрушается в точке отправления при проведении измерения, после чего воссоздаётся в точке приёма.
• Квантовая запутанность (Квантовая нелокальность, «Квантовое Вуду») — квантовомеханическое явление, при котором квантовые состояния двух или большего числа объектов оказываются взаимозависимыми (например, можно получить пару фотонов, находящихся в запутанном состоянии, и тогда если при измерении спина первой частицы спиральность оказывается положительной, то спиральность второй всегда оказывается отрицательной, и наоборот).
• Парадокс Эйнштейна — Подольского — Розена: могут ли далёкие друг от друга события влиять друг на друга (в квантовой механике)?
• Парадокс Клейна возникает при рассмотрении задачи о туннелировании релятивистской частицы через высокий потенциальный барьер. При решении уравнения Дирака вероятность прохождения частицы через потенциальный барьер, высота которого больше, чем удвоенная энергия покоя частицы, стремится к единице, независимо от высоты барьера.
• Квантовый парадокс Зенона («Парадокс незакипающего чайника», связанный с аксиомой идеального измерения) — метрологический парадокс квантовой механики, заключающийся в том, что время распада метастабильного квантового состояния некоторой системы с дискретным энергетическим спектром прямо зависит от частоты событий измерения её состояния. В предельном случае нестабильная частица в условиях частого наблюдения за ней никогда не может распасться.
• Кот Шрёдингера. Квантовый парадокс: кот жив или мёртв перед тем, как мы на него посмотрим? Связанный с ним парадокс друга Вигнера.
• Надбарьерное отражение — этот термин употребляется, чтобы описать невозможное в классической физике явление отражения от потенциального барьера, высота которого меньше полной энергии частицы.
• Теорема о запрете клонирования — утверждение квантовой теории о невозможности создания идеальной копии произвольного неизвестного квантового состояния.
• Обменное взаимодействие взаимодействие тождественных частиц в квантовой механике, приводящее к зависимости значения энергии системы частиц от её полного спина. Представляет собой чисто квантовый эффект, исчезающий при предельном переходе к классической механике.

[править] Связанные с путешествиями во времени

• Парадокс происхождения ставит вопрос о происхождении объектов или информации при путешествиях в прошлое.
• Парадокс убитого дедушки: вы перемещаетесь в прошлое и убиваете своего дедушку до того, как он познакомился с Вашей бабушкой. Из-за этого Вы не сможете появиться на свет и, следовательно, не сможете убить своего дедушку.
• Парадокс предопределения: человек попадает в прошлое, имеет половую связь со своей прабабушкой и зачинает своего дедушку. В результате получается череда потомков, включая родителя этого человека и его самого. Следовательно, если бы он не путешествовал в прошлое, его бы вообще не существовало.
• Парадокс конечного прошлого и бесконечного будущего (англ.): парадокс о путешествии в прошлое. Бесконечное число путешественников в ограниченный отрезок времени прошлого. Если машина, на которой возможно перемещение в прошлое, всё-таки будет изобретена, количество путешественников из бесконечного будущего будет соответственно бесконечным, в конечный отрезок прошлого.

[править] Гидродинамические

[править] Термодинамические

• Тепловая смерть вселенной: в 1850 г. немецкий физик Р. Клаузиус «… пришёл к выводу, что в природе теплота переходит от тёплого тела к холодному… Состояние Вселенной должно всё больше изменяться в определённом направлении… Эти представления развил английский физик Уильям Томсон, согласно которому все физические процессы во Вселенной сопровождаются превращением световой энергии в теплоту». Следовательно, Вселенную ожидает «тепловая смерть», поэтому бесконечное существование Вселенной во времени невозможно.
• Парадокс теплообмена: две одинаковые массы воды имеют разную температуру. Можно ли путём теплообмена нагреть более холодную воду до более высокой температуры, чем конечная температура охлаждаемой воды? Ведь как известно, тепло может переходить только от более нагретого тела к более холодному.
• Парадокс Гиббса: в идеальном газе является ли энтропия экстенсивной (аддитивной) переменной?
• Парадокс Лошмидта: почему есть неизбежный рост энтропии, хотя физические законы инвариантны относительно инверсии времени?
• Парадокс перемешивания — относительно энтропии системы до и после перемешивания.
• Парадокс Мпембы: горячая вода (при некоторых условиях) может замёрзнуть быстрее, чем холодная. Хотя при этом она должна пройти температуру холодной воды в процессе замерзания.
• Демон Максвелла: при смешении холодного с горячим холодное станет холоднее, а горячее дополнительно нагреется.
• Парадокс Шмидта: — обнаруженное в 1917 году противоречие между наблюдаемым турбулентным потоком тепла в приземном слое и теорией теплопроводности в атмосфере.

[править] Другие

• Корпускулярно-волновой дуализм — свет может рассматриваться либо как электромагнитная волна, скорость распространения в вакууме которой постоянна, либо как поток фотонов — частиц, обладающих определённой энергией, импульсом, собственным моментом импульса и нулевой массой.
• Парадокс Браеса: устройство, добавляющее мощность сети, может уменьшить общую производительность.
• Парадокс Кэррола (англ.): момент инерции палочки должен быть равен нулю, но он не равен.
• Парадокс Денни: живущие на поверхности воды членистоногие, согласно расчётам, не могут двигаться по поверхности, что противоречит природе.
• Парадокс интернета: вероятность существования нужной информации в Интернете возрастает, а возможность её найти уменьшается.
• Парадокс Ферми: если многие другие разумные существа присутствуют во Вселенной, как это можно предположить, тогда где они? Почему они не дают о себе знать (намеренно или случайно, искусственными излучениями)?
• Фотометрический парадокс (Парадокс звёздного неба, Парадокс Шезо — Ольберса): почему ночное небо чёрное, хотя в нём бесконечное число звёзд?
• Апория Зенона «Ахиллес и черепаха»: быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса, так как пока он переместится в точку, где была черепаха, она успеет продвинуться хоть немного вперёд.

• Проблема курицы и яйца: что было раньше — курица или яйцо? С одной стороны, для появления курицы необходимо яйцо, с другой — для появления яйца нужна курица.
• Тотальная казнь, или парадокс смертной казни: убийство в некоторых странах карается смертной казнью. Но, исполняя приговор, государство (то есть все его жители) становятся убийцами и должны быть приговорены к смерти.
• Парадокс эпикурейцев, или Проблема зла: кажется, что существование зла несовместимо с существованием всемогущего и заботливого Бога.
• Парадокс Ньюкома — парадоксы всезнания:
  • Почему можно выиграть у противника, знающего всё?
• Парадокс Хаттона: если кто-то спрашивает себя: «Сплю ли я?», то это доказывает, что он спит, то что это доказывает во время бодрствования?
• Парадокс либеральности (англ.): «минимальная свобода» не является равновесной по Парето.
• Аддитивность счастья (англ.): что лучше: большая группа людей, живущая сносной жизнью, или небольшая, живущая счастливо?
• Парадокс Мура (англ.): «Идёт дождь, но я не верю в это».
• Парадокс нигилизма (англ.): если правды не существует, то утверждение «правды не существует» верно, что доказывает его неверность.
• Парадокс всемогущества: может ли всемогущее существо создать камень, который оно само не сможет поднять?
• Довольно близок к предыдущему Парадокс непреодолимой силы (англ.): что будет, если непреодолимая сила подействует на несдвигаемый объект? (Оба эти парадокса, после некоторого анализа, могут быть признаны парадоксами противоречивых посылок (англ.), либо в житейском смысле посылки будут уточнены как «непреодолимая ранее сила», воздействуя на «несдвигаемый ранее объект», даст невиданное ранее.)
• Стрела Зенона: летящая стрела каждый момент времени занимает определенное положение в пространстве. Когда же она перемещается из одного положения в другое?
• Дихотомия: «Вы никогда не попадёте из точки А в точку Б, так как вы должны будете пройти половину пути, потом половину оставшейся половины, и так бесконечное число раз».

[править] Экономические

См. также: Category:Economics paradoxes(англ.)

• Парадокс Алле: изменение возможного дохода, который разделён между несколькими альтернативами, влияет на выбор людей между этими альтернативами, что противоречит теории ожидаемой полезности.
• Парадокс Базермана (Феномен Базермана: как продать 20 долларов за 204?).
• Парадокс бережливости: если каждый будет экономить деньги во время экономического спада, то совокупный спрос упадёт и в результате уменьшатся суммарные накопления населения.
• Парадокс Бертрана — ситуация, когда два олигополиста, конкурируя между собой и достигнув равновесия Нэша, оказываются с нулевой прибылью.
• Парадокс Гибсона (англ.): почему процентные ставки и цены скоррелированы?
• Парадокс Коперника — Грешема: плохие деньги вытесняют хорошие, если они имеют одинаковую цену.
• Парадокс Гиффена: если цены на хлеб начнут повышаться, люди станут покупать его больше.
• Парадокс Джевонса: повышение эффективности ведёт к ещё бо́льшему повышению спроса.
• Парадокс Кондорсе — парадокс теории общественного выбора: правило простого большинства не в состоянии обеспечить транзитивность бинарного отношения общественного предпочтения среди выбираемых вариантов. В силу нетранзитивности результат может зависеть от порядка голосования, что даёт возможность манипуляции выбором большинства. Обобщён теоремой «о невозможности» Эрроу в 1951 г.
• Парадокс Леонтьева: некоторые страны экспортируют трудозатратные товары, а импортируют капиталозатратные, что является контрпримером к теории Хекшера — Олина.
• Парадокс продуктивности (англ.): продуктивность работника уменьшается, несмотря на улучшения в технологиях.
• Парадокс Триффина: для формирования долларовых резервов других стран необходимо, чтобы в США постоянно наблюдался дефицит платёжного баланса. Но дефицит платёжного баланса подрывает доверие к доллару и снижает его ценность в качестве резервного актива.
• Парадокс ценности: почему вода стоит дешевле алмазов, хотя потребность человека в ней гораздо больше, чем в алмазах?
• Парадокс Эджворта (англ.): может не существовать равновесия, если мощности производств ограничены.
• Парадокс Элсберга (англ.): люди предпочитают известный, хотя и бо́льший, риск неизвестному риску, что противоречит теории ожидаемой полезности.
• Информационный парадокс Эрроу(англ.)русск.: потенциальный потребитель хочет знать о приобретаемом товаре/услуге как можно больше достоверной информации, продавец же, владеющий интеллектуальной собственностью, не хочет безвозмездно раскрывать характеристики товара, и поэтому склонен обманывать покупателя, который в этом случае вынужден принимать решение на основе недостоверной информации.

[править] Психофизиологические

Список парадоксов — Традиция

Материал из свободной русской энциклопедии «Традиция»

Это список парадоксов, сгруппированных по темам.

Логические (кроме математических)[править]

Парадоксы самореференции (самоотносимости)[править]

Это хорошо известный (и хорошо изученный) класс противоречий, возникаемых из-за ссылки на самоё себя.

• Парадокс Берри: Фраза «наименьшее число, которое нельзя описать менее, чем десятью словами» описывает это число девятью словами.
• Парадокс Карри: «Если это предложение верно, то через неделю наступит конец света»
• Парадокс Эпименида: Критянин говорит: «Все критяне — лжецы»
• Парадокс исключений: «Если у каждого правила есть исключения, то каждое правило должно иметь хотя бы одно исключение, кроме этого» …а это не исключение к правилу, которое утверждает, что у каждого правила есть исключения?
• Парадокс Греллинга-Нельсона: Является ли слово «гетерологичный», означающее «неприменимый к самому себе», гетерологичным словом? (Близко к Парадоксу Рассела)
• Парадокс Гегеля (Гегель, Георг Вильгельм Фридрих): «История учит человека тому, что человек ничему не учится из истории»
• Парадокс лжеца: «Это предложение ложно»
• Комбинатор Y в λ-исчислении и комбинаторной логике был назван парадоксальным комбинатором так как он связан с самоотносимостью.
• Парадокс Петрония: «Ограничивайте себя во всех вещах, даже в ограничении»
• Парадокс Квина: «…влечёт за собой ложность, будучи добавленным к собственному цитированию» влечёт за собой ложность, будучи добавленным к собственному цитированию
• Парадокс Эватла (софизм Эватла): Протагор взял ученика Эватла при условии, что тот ему заплатит, когда выиграет первое дело. Случилось так, что Протагор подал иск на Эватла за то, что тот ему долго не платит. Должен ли Эватл заплатить, если он выиграет это дело (хотя выигрыш означает, что Эватл ничего не должен Протагору)?
• Парадокс Рассела: Содержит ли множество всех таких множеств, которые не содержат себя, самого себя? Рассел популяризовал его в форме парадокса брадобрея: «Брадобрей бреет всех людей, которые не бреются сами. Бреет ли он себя?»
• Парадокс Ричарда: Если сопоставить все свойства чисел с числами, то можно определить такое свойство, которому не будет соответствовать никакое число.
• Прикажите слуге не слушаться Вас. Не слушаясь Вас, он ослушается приказа, т.к. он исполняет его, не слушаясь Вас.
• Парадокс всемогущего безумного интеллекта: «непонимающий — думает по причине его непонимания, поэтому абсолютно всё понимающий — делает это абсолютно ничего не думая!»

Неопределённые[править]

• Корабль Тесея Если каждый элемент корабля был заменён хотя бы один раз, можно ли считать корабль прежним кораблём?
• Парадокс кучи: В какой момент куча перестанет быть кучей, если отнимать от неё по одной песчинке? Или, в какой конкретно день какой-либо человек становится лысым?

Математические и статистические[править]

См. также: Категория:Математические парадоксы

• Парадоксы пропорционального представительства в США (en): Некоторые системы представительства могут иметь последствия, идущие против интуиции:
• Парадокс голосования (Парадокс Кондорсе/Arrow’s paradox(англ.)) Нельзя совместить все требования к избирательной системе в одной системе.
• Закон Бенфорда (англ.): Во многих списках чисел из произвольных реальных источников, большинство чисел начинаются с цифры 1.
• Парадокс лифта: Лифты чаще всего ходят в одном направлении — от середины здания вниз к подвалу и вверх к чердаку
• Парадокс ожидания: Почему иногда приходится ждать автобус дольше, чем нужно. (пояснение смотрите в англ. статье Renewal theory)
• Парадокс интересных чисел. Первое неинтересное число интересно само по себе этим фактом. Поэтому неинтересных чисел не существует.
• Игра в нетранзитивные кости (англ.): существует набор из 3 костей А, В и С таких, что чаще всего на А выпадает бо́льшее число, чем на В; на В чаще выпадает бо́льшее число, чем на С; на С чаще выпадает бо́льшее число, чем на А.
• Парадокс Линдли (англ.): маленькие ошибки в нулевой гипотезе сильно возрастают, если анализируются большие массивы данных, приводя к ложным, но одновременно точным со статистической точки зрения результатам.
• Парадокс недоношенности: Низкий вес при рождении и курение матери приводят к большой смертности. Дети курящих родителей имеют более низкий вес при рождении, однако маловесящие дети курящих родителей имеют более низкую смертность, чем другие маловесящие дети.
• Парадокс пропавшего доллара: Неправильная логика приводит к тому, что один доллар «пропадает».
• Парадокс корреляции: Вполне возможно сделать ложные заключения из корреляции. К примеру, города с бо́льшим количеством церквей имеют больше преступлений, потому что оба фактора следуют из бо́льшего населения. Это называется ложной корреляцией.
• Феномен Уилла Роджерса (англ.): математическое понятие среднего, определённое как среднее арифметическое, или как медиана — неважно, приводит к парадоксальному результату — например, возможно переместить статью из Википедия в Викицитатник так, чтобы средняя длина статьи увеличилась на обоих сайтах!
• Парадокс Райта: Ребёнок стареет быстрее, чем старик, так как удвоение возраста — более частое явление в начале процесса, чем в конце.

Вероятностные[править]

См. также: Категория:Вероятностные парадоксы

• Парадокс Берксона (англ.): два независимых события становятся условно зависимыми при условии, что хотя бы одно из них произошло.
• Парадокс Бертрана (теория вероятности) (англ.): Различные определения случайной величины, основанные на «здравом смысле», дают различные результаты.
• Парадокс дней рождения : Какая вероятность того, что у двоих учеников из одного класса день рождения совпадает? Оказывается — больше половины, если учеников больше 23!
• Парадокс Бореля (англ.): Плотность условной вероятности не инвариантна при преобразованиях координат.
• Пол второго ребёнка (парадокс) (англ.): Если один из двух детей в семье — мальчик, какова вероятность того, что второй ребёнок — девочка?
• Парадокс Монти Холла: Неочевидное следствие условной вероятности. По сути дела то же, что и задача трёх узников (en).
• Парадокс Симпсона (англ.): Основные интересы подобщества могут оказаться совсем не основными во всём обществе. Поэтому если два ряда данных соответствуют одной определённой гипотезе, будучи объединёнными, они могут соответствовать противоположной гипотезе.
• Задача спящей красавицы (англ.): Вероятностная задача, которая может иметь в качестве ответа 1/2 или 1/3 в зависимости от того, с какой стороны рассматривать вопрос.
• Задача трёх карточек (англ.): Истинная вероятность того, что обратная сторона случайно выбранной карты окажется того же цвета, что и верхняя, противоречит интуитивной оценке такой вероятности некоторыми людьми.
• Парадокс двух конвертов (англ.): Вам дают два одинаковых конверта и говорят, что один из них содержит в два раза больше денег, чем другой. Вы должны открыть один из них, проверить содержимое, а затем, не открывая другой, решить, какой из конвертов взять.
• Парадокс пари (англ.). В некоторых ситуациях выгодно спорить обоим противникам, ибо оба имеют бо́льшие шансы на победу, чем на проигрыш.
• Парадокс Ходжсона (англ.): Отношение двух распределённых гауссово случайных переменных не имеет ни математического ожидания, ни дисперсии
• Парадокс де Мере
• Парадокс раздела ставки
• Парадокс независимости
• Парадокс бриджа и лотереи
• Парадокс раздачи подарков
• Санкт-Петербургский парадокс
• Парадокс смертности населения
• Парадокс де Муавра
• Парадокс транзитивности
• Парадокс страхования
• Парадокс смертной казни
• Парадокс психологических ценностей

Связанные со случайными процессами[править]

Связанные с бесконечностью[править]

Геометрические или топологические[править]

• Парадокс Банаха — Тарского: Возможно разрезать шар на 5 частей, сложить их по-другому и получится два шара такого же радиуса, как и первоначальный.
• Рог Гавриила (англ.) или «труба Торричелли»: Простое тело, имеющее конечный объём, но бесконечную площадь поверхности. Множество Мандельброта и различные другие фракталы имеют конечную площадь, но бесконечный периметр. Более того на границе множества Мандельброта не существует двух различных точек, между которыми конечное расстояние по периметру, что можно понять так: если Вы пойдёте вдоль границы этого множества, Вы нисколько не сдвинетесь из одной точки.
• Парадокс Хаусдорфа: Существует счётное подмножество C на сфере S такое, что S\C можно разбить на две копии самого себя.
• Парадокс побережья (англ.): периметр континента не может быть корректно определён (не может быть сопоставлен конкретному числу)

Связанные с выбором[править]

• Парадокс Абилина (англ.): Бывает, что люди принимают решения основанные не на том, что они сами хотят, но на том, что они думают, что другие хотят. В результате получается, что каждый делает что-то, что никому на самом деле не нужно.
• Буриданов осёл: Как можно совершить рациональный выбор между двумя вещами, имеющими одинаковую ценность?
• Парадокс контроля: Человек не может быть свободен от контроля, ибо чтобы быть свободным от контроля, нужно контролировать себя.
• «Вилка» Мортона (англ.): Выбор из двух плохих альтернатив («выбор из двух зол»).
• Загадка Кавки о яде (англ.): Может ли человек быть намеренным выпить смертельный яд, если намерение — единственная вещь, которая нужна для получения награды?

• SAR-парадокс (англ.): Исключения из правила, что малое изменение в молекуле влечёт за собой малое изменение в химическом поведении, часто очень глубоки по смыслу.
• Парадокс Левинталя (англ.): Промежуток времени, за который протеиновая цепочка приходит к своему скрученному состоянию, на много порядков меньше, чем оно могло бы быть, если она просто перебирала все возможные конфигурации.

Смотрите статью Физические парадоксы (англ.).

Из теории относительности и квантовой механики[править]

• Парадокс Архимеда. Огромный корабль может плавать в нескольких литрах воды.
• Парадокс космического корабля: Разорвётся ли струна, соединяющая релятивистские объекты?
• Парадокс Эйнштейна-Подольского-Розена: Могут ли далёкие друг от друга события влиять друг на друга (в квантовой механике)?
• ГЗК-парадокс: Наблюдаемые высокоэнергетичные космические лучи, похоже, нарушают предел Грайзена-Зацепина-Кузьмина (англ.), который является следствием СТО.
• Парадокс лестницы: Может ли лестница засчёт релятивистского сокращения длины поместиться в меньший по размеру гараж?
• Кот Шрёдингера. Квантовый парадокс: кот жив или мёртв перед тем, как мы на него посмотрим?
• Парадокс близнецов: Когда близнец-путешественник вернулся, он стал моложе или старше, чем его брат, который оставался на Земле?
• Парадокс подводной лодки: Сила Архимеда на релятивистский (англ.) объект (типа пули) изменяется при переходе от системы отсчёта, в которой покоится пуля, в систему отсчёта, в которой покоится жидкость.
• Парадокс Эренфеста о кинематике абсолютно твёрдого вращающегося диска.

Связанные с путешествиями во времени[править]

• Парадокс происхождения ставит вопрос о происхождении объектов или информации при путешествиях в прошлое.
• Парадокс дедушки: Вы перемещаетесь в прошлое и убиваете своего дедушку до того, как он познакомился с Вашей бабушкой. Из-за этого Вы не сможете появиться на свет и, следовательно, не сможете убить своего дедушку.
• Парадокс предопределения: Человек попадает в прошлое и брюхатит свою пра-пра-прабабушку. В результате получается череда потомков, включая родителя этого человека и его самого. Следовательно, если бы он не путешествовал в прошлое, его бы вообще не существовало.
• Парадокс разногласия прошлого и будущего времён: «говоря эти слова ровно десять секунд, я этим, по прошествии их, изменю своё будущее!» (Не понятно в какой момент, прошлое — становится настоящим, а настоящее — становится будущим, временем).
• Парадокс золотой рыбки: Мальчик поймал золотую рыбку исполняющую желания, и попросил её исполнить его желание — сделать так, что бы уже произошедшая поимка им этой рыбки, вообще бы не случилась, и не произошла!…
• Парадокс наполняющегося не наполняемого стакана: «пустой стакан начинает наполняться лишь только в тот момент, когда он ещё является пустым, иначе если бы это было не так, то он в момент начала наполнения его, уже не должен был бы быть пустым, но не являясь пустым, он не может начать наполняться!» (не понятно в какой момент покоящиеся относительно друг друга физические тела, начинают относительно друг друга своё движение)

Гидродинамические[править]

Другие[править]

• Исчезновение информации в чёрной дыре: Чёрная дыра нарушает общепризнанную научную догму — что информация не уничтожается.
• Парадокс Браеса: Устройство, добавляющее мощность сети, может уменьшить общую производительность.
• Парадокс Майкла Кэррола: Момент инерции палочки должен быть равен нулю, но он не равен.
• Парадокс Денни: Живущие на поверхности воды членистоногие, согласно расчётам, не могут двигаться по поверхности, что противоречит природе.
• Парадокс Ферми: Если многие другие разумные существа присутствуют во Вселенной, как это можно предположить, тогда где они? Почему они не дают о себе знать (намеренно или случайно, искусственными излучениями)?
• Парадокс Гиббса: В идеальном газе является ли энтропия экстенсивной (аддитивной) переменной?
• Парадокс Лошмидта: Почему есть неизбежный рост энтропии, хотя физические законы инвариантны относительно инверсии времени?
• Парадокс перемешивания — относительно энтропии системы до и после перемешивания.
• Парадокс Мпембы: Горячая вода (при некоторых условиях) может замёрзнуть быстрее, чем холодная. Хотя при этом она должна пройти температуру холодной воды в процессе замерзания.
• Фотометрический парадокс: Почему ночное небо — чёрное, хотя в нём бесконечное число звёзд?
• Парадокс велосипедиста: Велосипедист при его езде на велосипеде, и бегун при его беге, затрачивают на совершение ими полезной работы одинаковую их энергию, но велосипедист при этом, по сравнению с бегуном, совершает гораздо большую его полезную работу.

• Тотальная казнь, или парадокс смертной казни: Убийство в некоторых странах карается смертной казнью. Но совершая её, государство (то есть все его жители) становятся убийцами и должны быть приговорены к смерти.
• Парадокс эпикурейцев, или Проблема зла: Кажется, что существование зла несовместимо с существованием всемогущего и заботливого Бога.
• Парадокс Ньюкома — парадоксы всезнания:
  • Если существует знающее всё существо (Бог), то невозможно иметь свободную волю, так как это существо будет знать, что вы хотите предпринять, а значит вы не можете принять решение, потому что оно уже сделано до вас.
  • Почему можно выиграть у противника, знающего всё?
• Парадокс Хаттона: Если кто-то спрашивает себя «Сплю ли я?», то это доказывает, что он спит, то что это доказывает во время бодрствования?
• Парадокс либеральности (англ.): «Минимальная свобода» не является равновесной по Парето.
• Аддитивность счастья: Что лучше: большая группа людей, живущая сносной жизнью, или небольшая, живущая счастливо?
• Парадокс Мура: «Идёт дождь, но я не верю в это»
• (англ.): Если правда не существует, то утверждение «правда не существует» верно, что доказывает его неверность.
• Парадокс всемогущества: Может ли всемогущее существо создать камень, который оно само не сможет поднять?
• Довольно близок к предыдущему Парадокс непреодолимой силы: Что будет, если непреодолимая сила подействует на несдвигаемый объект? (Оба эти парадокса, после некоторого анализа, могут быть признаны парадоксами противоречивых посылок (англ.))
• Парадокс гедонизма: Когда человек занимается только своим счастьем, он несчастен; но, занимаясь другими вещами, он может быть счастливым.
• Апории Зенона: «Вы никогда не попадёте из точки А в точку Б, т.к. вы должны будете пройти половину пути, потом половину оставшейся половины, и так бесконечное число раз»

См. также: (англ.)

• Парадокс Бертрана — ситуация, когда два олигополиста, конкурируя между собой и достигнув равновесия Нэша, оказываются с нулевой прибылью.
• Парадокс Алле (англ.): Изменение возможного дохода, который разделён между несколькими альтернативами, влияет на выбор людей между этими альтернативами, что противоречит теории ожидаемой пользы (англ.).
• Парадокс ценности: Почему вода стоит дешевле алмазов, хотя потребность человека в ней гораздо больше, чем в алмазах?
• Парадокс Эджворта (англ.): Может не существовать равновесия, если мощности производств ограничены.
• Парадокс Элсберга: Люди предпочитают известный, хотя и бо́льший, риск неизвестному риску, что противоречит теории ожидаемой пользы (англ.).
• Парадокс Гибсона (англ.): Почему процентные ставки и цены скоррелированы?
• Парадокс Гиффена (англ.): Если цены на хлеб начнут повышаться, люди станут покупать его больше.
• Парадокс Джевонса (англ.): Повышение эффективности ведёт к ещё бо́льшему повышению спроса.
• Парадокс Леонтьева: Некоторые страны экспортируют трудозатратные товары, а импортируют капиталозатратные, что является контрпримером к теории Хекшера-Олина (англ.).
• Парадокс бережливости: Если каждый будет экономить деньги во время экономического спада, то совокупный спрос упадёт и в результате уменьшатся суммарные накопления населения.
• Парадокс Паррондо (англ.): Возможно выиграть, играя поочерёдно в две заведомо проигрышные игры.
• Парадокс продуктивности: Продуктивность работника уменьшается, несмотря на улучшения в технологиях.
• Парадокс Санкт-Петербурга: Люди вряд ли будут играть в эту игру, хотя математическое ожидание выигрыша в ней бесконечно велико.

Список парадоксов — Википедия

Это список парадоксов, сгруппированных по темам.

Парадо́кс (от др.-греч. παράδοξος — неожиданный, странный; от παρα-δοκέω — кажусь) — ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения. Следует различать парадокс и апорию: последняя, в отличие от парадокса, является вымышленной, логически верной ситуацией (высказыванием, утверждением, суждением или выводом), которая не может существовать в реальности.

Логические (кроме математических)[править]

Парадоксы самореференции (самоотносимости)[править]

Это хорошо известный (и хорошо изученный) класс противоречий, возникающих в высказываниях, которые содержат определение чего-либо, неявно ссылающееся на само себя.

• Парадокс Берри: фраза «наименьшее число, которое нельзя описать менее чем десятью словами» описывает это число девятью словами.
• Парадокс Карри: «Если это утверждение верно, то русалки существуют».
• Парадокс крокодила: Крокодил украл ребёнка и обещал матери отдать его, если она верно ответит, отдаст ли крокодил ей ребёнка.
• Парадокс Эпименида: критянин говорит: «Все критяне — лжецы».
• Парадокс исключений (англ.): «Если у каждого правила есть исключения, то каждое правило должно иметь хотя бы одно исключение, кроме этого» … а это не исключение к правилу, которое утверждает, что у каждого правила есть исключения?
• Парадокс Греллинга-Нельсона: является ли слово «гетерологичный», означающее «неприменимый к самому себе», гетерологичным словом? (Близко к Парадоксу Рассела.)
• Парадокс Гегеля: «История учит человека тому, что человек ничему не учится из истории».
• Y-комбинатор в лямбда-исчислении и комбинаторной логике был назван парадоксальным комбинатором так как он связан с самоотносимостью.
• Парадокс Петрония: «Ограничивайте себя во всех вещах, даже в ограничении».
• Парадокс Квина (англ.): «… влечёт за собой ложность, будучи добавленным к собственному цитированию» влечёт за собой ложность, будучи добавленным к собственному цитированию.
• «Парадокс Эватла» (софизм Эватла): Протагор взял ученика Эватла при условии, что тот ему заплатит, когда выиграет первое дело. Случилось так, что Протагор подал иск на Эватла за то, что тот ему долго не платит. Должен ли Эватл заплатить, если он выиграет это дело?
• Парадокс Рассела: содержит ли множество всех множеств, которые не содержат себя, само себя? Рассел популяризовал его в форме «парадокса брадобрея»: «Брадобрей бреет только тех людей, которые не бреются сами. Бреет ли он себя?»
• Парадокс Ришара: если сопоставить все свойства чисел с числами, то можно определить такое свойство, которому не будет соответствовать никакое число.
• Парадокс всемогущества: может ли всемогущее существо создать камень, который оно само не сможет поднять?

Парадоксы определений[править]

• Корабль Тесея: если каждый элемент корабля был заменён хотя бы один раз, можно ли считать корабль прежним кораблём?
• Парадокс кучи. В какой момент куча перестанет быть кучей, если отнимать от неё по одной песчинке?
• Парадокс лысого: если волосы с головы выпадают по одному, с какого момента человек становится лысым?
• Парадокс интересных чисел: наименьшее неинтересное натуральное число интересно само по себе этим фактом, но тогда оно не относится к неинтересным.

Математические и статистические[править]

См. также: Категория:Математические парадоксы

• Парадоксы пропорционального представительства в США (en): некоторые системы представительства могут иметь последствия, идущие против интуиции:
• Парадокс голосования (Парадокс Эрроу): нельзя совместить все требования к избирательной системе в одной системе.
• Закон Бенфорда: во многих списках чисел из произвольных реальных источников большинство чисел начинаются с цифры 1.
• Парадокс лифта: лифты чаще всего ходят в одном направлении — от середины здания вниз к подвалу и вверх к чердаку
• Парадокс ожидания: почему иногда приходится ждать автобус дольше, чем нужно. (пояснение смотрите в англ. статье Renewal theory)
• Игра в нетранзитивные кости: существует набор из 3 костей А, В и С таких, что чаще всего на А выпадает бо́льшее число, чем на В; на В чаще выпадает бо́льшее число, чем на С; на С чаще выпадает бо́льшее число, чем на А.
• Игра Пенни: нетранзитивный парадокс, разновидность игры в нетранзитивные кости.
• Парадокс Линдли (англ.): маленькие ошибки в нулевой гипотезе сильно возрастают, если анализируются большие массивы данных, приводя к ложным, но одновременно точным со статистической точки зрения результатам.
• Парадокс недоношенности (англ.): низкий вес при рождении и курение матери приводят к большой смертности. Дети курящих родителей имеют более низкий вес при рождении, однако маловесящие дети курящих родителей имеют более низкую смертность, чем другие маловесящие дети.
• Парадокс пропавшего доллара (англ.): неправильная логика приводит к тому, что один доллар «пропадает».
• Парадокс корреляции: вполне возможно сделать ложные заключения из корреляции. К примеру, города с бо́льшим количеством церквей имеют больше преступлений, потому что оба фактора следуют из бо́льшего населения. Это называется ложной корреляцией.
• Триада отрицательных корреляций в парадоксе голосования (Парадокс Кондорсе/Arrow’s paradox (англ.)): избиратель 1 ранжирует троих кандидатов в порядке А, В, С; избиратель 2 — в порядке В, С, А; избиратель 3 — в порядке С, А, В. Таким образом, любые две трети избирателей согласны между собой в сравнительной оценке двух третей кандидатов. Но коэффициент ранговой корреляции Спирмена между предпочтениями любых двух избирателей из этой тройки отрицателен и равен −0,5. Отрицательные же корреляции между рангами предпочтений у разных людей характеризуют, по смыслу понятия корреляции, скорее несогласие между этими людьми, чем их согласие.
• Феномен Уилла Роджерса: математическое понятие среднего, определённое как среднее арифметическое или медиана (неважно), приводит к парадоксальному результату — например, возможно переместить статью из Википедии в Викицитатник так, чтобы средняя длина статьи увеличилась на обоих сайтах!
• Парадокс маляра: бесконечную по площади пластинку можно окрасить конечным количеством краски.
• Парадокс Паррондо: возможно выиграть, играя поочерёдно в две заведомо проигрышные игры.
• Парадокс ряда 1−1+1−… (Ряд Гранди): имеется бесконечный ряд 1−1+1−… Какова его сумма? Можно доказать, что она равна 0, 1 или 0,5.
• Существует несколько доказательств, что сумма всех натуральных чисел 1 + 2 + 3 + 4 + … = −¹⁄₁₂.

Вероятностные[править]

См. также: Категория:Вероятностные парадоксы

• Парадокс Берксона: два независимых события становятся условно зависимыми при условии, что хотя бы одно из них произошло.
• Парадокс Бертрана: различные определения случайной величины, основанные на «здравом смысле», дают различные результаты.
• Парадокс дней рождения: какая вероятность того, что у двух учеников из одного класса день рождения совпадает? Оказывается — более 50 %, если учеников больше 23.

Загадка Монти Холла: в поисках автомобиля игрок выбирает дверь 1. Тогда ведущий открывает третью дверь, за которой находится коза, и предлагает игроку изменить свой выбор на дверь 2. Увеличиваются ли шансы игрока при выборе двери 2?

• Парадокс Бореля (англ.): плотность условной вероятности не инвариантна при преобразованиях координат.
• Пол второго ребёнка: если один из двух детей в семье — мальчик, какова вероятность того, что второй ребёнок — девочка?
• Парадокс Монти Холла: неочевидное следствие условной вероятности. По сути дела то же, что и задача трёх узников.
• Парадокс Симпсона: основные интересы подобщества могут оказаться совсем не основными во всём обществе. Поэтому если два ряда данных соответствуют одной определённой гипотезе, будучи объединёнными, они могут соответствовать противоположной гипотезе.
• Задача спящей красавицы: Вероятностная задача, которая может иметь в качестве ответа 1/2 или 1/3 в зависимости от того, с какой стороны рассматривать вопрос.
• Задача трёх карточек (англ.): истинная вероятность того, что обратная сторона случайно выбранной карты окажется того же цвета, что и верхняя, противоречит интуитивной оценке такой вероятности некоторыми людьми.
• Парадокс двух конвертов: вам дают два одинаковых конверта и говорят, что один из них содержит в два раза больше денег, чем другой. Вы должны открыть один из них, проверить содержимое, а затем, не открывая другой, решить, какой из конвертов взять.
• Парадокс пари: в некоторых ситуациях выгодно спорить обоим противникам, ибо оба имеют бо́льшие шансы на победу, чем на проигрыш.
• Парадокс Ходжсона (англ.): отношение двух распределённых гауссово случайных переменных не имеет ни математического ожидания, ни дисперсии
• Ошибка игрока (gambler’s fallacy) — (ложный вывод Монте-Карло) о том, что выгодно ставить на красное, если чёрное выпало 10 раз подряд.
• Санкт-Петербургский парадокс: люди вряд ли будут играть в эту игру, хотя математическое ожидание выигрыша в ней бесконечно велико.
• Парадокс закономерности: увидев явную закономерность в результатах серии испытаний (например, выпадение 10 000 раз подряд одного и того же варианта из двух возможных), мы будем склонны считать, что испытания не являются случайными. Однако появление любой другой последовательности из 10 000 значений в случайных испытаниях является настолько же маловероятным событием.

Связанные с бесконечностью[править]

Геометрические или топологические[править]

• Парадокс Банаха — Тарского: возможно разрезать шар на 5 частей, сложить их по-другому и получится два шара такого же радиуса, как и первоначальный.
• Квадратура круга Тарского: круг и квадрат равной площади равносоставлены при конечном разбиении.
• Рог Гавриила (англ.) или «труба Торричелли»: простое тело, имеющее конечный объём, но бесконечную площадь поверхности. Множество Мандельброта и различные другие фракталы имеют конечную площадь, но бесконечный периметр. Более того на границе множества Мандельброта не существует двух различных точек, между которыми конечное расстояние по периметру, что можно понять так: если Вы пойдёте вдоль границы этого множества, Вы нисколько не сдвинетесь из одной точки.
• Парадокс Хаусдорфа: существует счётное подмножество C на сфере S такое, что S\C можно разбить на две копии самого себя.
• Парадокс побережья (англ.): периметр континента не может быть корректно определён (не может быть сопоставлен конкретному числу)

Парадокс Смейла утверждает, что можно вывернуть (с самопересечениями, но без складок) сферу в трёхмерном пространстве. Одна из промежуточных конфигураций, Поверхность Морина (англ.), видна на рисунке.

• Парадокс Смейла: сфера топологически может быть вывернута наизнанку.
• Исчезновение клетки: при различных вариантах складывания одних и тех же элементов в одинаковую фигуру «исчезновение» элемента наглядно демонстрирует, что площади получаемых фигур различны. (Правда, можно заметить, что исходная и конечная фигуры различны — гипотенуза треугольников является не прямой линией, а разными ломанными. Этим и объясняется разница площадей, поэтому данный парадокс относится к визуальным иллюзиям.)

Связанные с выбором[править]

• Парадокс Абилина: бывает, что люди принимают решения, основанные не на том, что они сами хотят, но на том, что они думают, что другие хотят. В результате получается, что каждый делает что-то, что никому на самом деле не нужно.
• Буриданов осёл: как можно совершить рациональный выбор между двумя вещами, имеющими одинаковую ценность?
• Парадокс контроля (англ.): человек не может быть свободен от контроля, ибо чтобы быть свободным от контроля, нужно контролировать себя.
• Вилка Мортона: выбор из двух плохих альтернатив («выбор из двух зол»).
• Загадка Кавки о яде (англ.): может ли человек быть намеренным выпить несмертельный яд, если намерение — единственная вещь, которая нужна для получения награды?
• Дилемма заключённого: при некоторых условиях оптимальная стратегия поведения каждого игрока, если каждый игрок исходит из эгоистичных соображений, оказывается проигрышной для группы в целом и для каждого игрока в отдельности.

Смотрите статью Парадоксы квантовой механики, Физические парадоксы (англ.).

Из теории относительности и квантовой механики[править]

• Парадокс Белла: разорвётся ли струна, соединяющая релятивистские объекты?
• Парадокс Эйнштейна-Подольского-Розена: могут ли далёкие друг от друга события влиять друг на друга (в квантовой механике)?
• ГЗК-парадокс: наблюдаемые высокоэнергетичные космические лучи, похоже, нарушают предел Грайзена-Зацепина-Кузьмина, который является следствием СТО.
• Парадокс лестницы: Может ли лестница за счёт релятивистского сокращения длины поместиться в меньший по размеру гараж?
• Кот Шрёдингера. Квантовый парадокс: кот жив или мёртв перед тем, как мы на него посмотрим? Связанный с ним парадокс друга Вигнера.
• Парадокс близнецов: когда близнец-путешественник вернулся, он стал моложе или старше, чем его брат, который оставался на Земле?
• Парадокс субмарины: сила Архимеда на релятивистский (англ.) объект (типа пули) изменяется при переходе от системы отсчёта, в которой покоится пуля, в систему отсчёта, в которой покоится жидкость.
• Парадокс Эренфеста о кинематике абсолютно твёрдого вращающегося диска.
• Исчезновение информации в чёрной дыре: чёрная дыра нарушает общепризнанную научную догму — что информация не уничтожается.

Связанные с путешествиями во времени[править]

• Парадокс происхождения (англ.) ставит вопрос о происхождении объектов или информации при путешествиях в прошлое.
• Парадокс убитого дедушки: вы перемещаетесь в прошлое и убиваете своего дедушку до того, как он познакомился с Вашей бабушкой. Из-за этого Вы не сможете появиться на свет и, следовательно, не сможете убить своего дедушку.
• Парадокс предопределения (англ.): человек попадает в прошлое, имеет половую связь со своей прабабушкой и зачинает своего дедушку. В результате получается череда потомков, включая родителя этого человека и его самого. Следовательно, если бы он не путешествовал в прошлое, его бы вообще не существовало.
• Парадокс конечного прошлого и бесконечного будущего (англ.): парадокс о путешествии в прошлое. Бесконечное число путешественников в ограниченный отрезок времени прошлого. Если машина, на которой возможно перемещение в прошлое, всё-таки будет изобретена, количество путешественников из бесконечного будущего будет соответственно бесконечным, в конечный отрезок прошлого.

Гидродинамические[править]

Термодинамические[править]

• Тепловая смерть вселенной: в 1850 г. немецкий физик Р. Клаузиус «… пришёл к выводу, что в природе теплота переходит от тёплого тела к холодному… Состояние Вселенной должно всё больше изменяться в определённом направлении… Эти представления развил английский физик Уильям Томсон, согласно которому все физические процессы во Вселенной сопровождаются превращением световой энергии в теплоту». Следовательно, Вселенную ожидает «тепловая смерть», поэтому бесконечное существование Вселенной во времени невозможно.
• Парадокс теплообмена: две одинаковые массы воды имеют разную температуру. Можно ли путём теплообмена нагреть более холодную воду до более высокой температуры, чем конечная температура охлаждаемой воды? Ведь как известно, тепло может переходить только от более нагретого тела к более холодному.
• Парадокс Гиббса: в идеальном газе является ли энтропия экстенсивной (аддитивной) переменной?
• Парадокс Лошмидта (англ.): почему есть неизбежный рост энтропии, хотя физические законы инвариантны относительно инверсии времени?
• Парадокс перемешивания (англ.) — относительно энтропии системы до и после перемешивания.
• Парадокс Мпембы: горячая вода (при некоторых условиях) может замёрзнуть быстрее, чем холодная. Хотя при этом она должна пройти температуру холодной воды в процессе замерзания.
• Демон Максвелла: при смешении холодного с горячим холодное станет холоднее, а горячее дополнительно нагреется.
• Парадокс Шмидта: — обнаруженное в 1917 году противоречие между наблюдаемым турбулентным потоком тепла в приземном слое и теорией теплопроводности в атмосфере.

Другие[править]

• Корпускулярно-волновой дуализм — свет может рассматриваться либо как электромагнитная волна, скорость распространения в вакууме которой постоянна, либо как поток фотонов — частиц, обладающих определённой энергией, импульсом, собственным моментом импульса и нулевой массой.
• Парадокс Браеса: устройство, добавляющее мощность сети, может уменьшить общую производительность.
• Парадокс Кэррола (англ.): момент инерции палочки должен быть равен нулю, но он не равен.
• Парадокс Денни: живущие на поверхности воды членистоногие, согласно расчётам, не могут двигаться по поверхности, что противоречит природе.
• Парадокс интернета: вероятность существования нужной информации в Интернете возрастает, а возможность её найти уменьшается.
• Парадокс Ферми: если многие другие разумные существа присутствуют во Вселенной, как это можно предположить, тогда где они? Почему они не дают о себе знать (намеренно или случайно, искусственными излучениями)?
• Фотометрический парадокс (Парадокс звёздного неба, Парадокс Шезо — Ольберса): почему ночное небо чёрное, хотя в нём бесконечное число звёзд?
• Апория Зенона «Ахиллес и черепаха»: быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса, так как пока он переместится в точку, где была черепаха, она успеет продвинуться хоть немного вперёд.

• Проблема курицы и яйца: что было раньше — курица или яйцо? С одной стороны, для появления курицы необходимо яйцо, с другой — для появления яйца нужна курица.
• Тотальная казнь, или парадокс смертной казни: убийство в некоторых странах карается смертной казнью. Но, исполняя приговор, государство (то есть все его жители) становятся убийцами и должны быть приговорены к смерти.
• Парадокс эпикурейцев, или Проблема зла: кажется, что существование зла несовместимо с существованием всемогущего и заботливого Бога.
• Парадокс Ньюкома — парадоксы всезнания:
  • Почему можно выиграть у противника, знающего всё?
• Парадокс Хаттона (англ.): если кто-то спрашивает себя: «Сплю ли я?», то это доказывает, что он спит, то что это доказывает во время бодрствования?
• Парадокс либеральности (англ.): «минимальная свобода» не является равновесной по Парето.
• Аддитивность счастья (англ.): что лучше: большая группа людей, живущая сносной жизнью, или небольшая, живущая счастливо?
• Парадокс Мура (англ.): «Идёт дождь, но я не верю в это».
• Парадокс нигилизма (англ.): если правды не существует, то утверждение «правды не существует» верно, что доказывает его неверность.
• Парадокс всемогущества: может ли всемогущее существо создать камень, который оно само не сможет поднять?
• Довольно близок к предыдущему Парадокс непреодолимой силы (англ.): что будет, если непреодолимая сила подействует на несдвигаемый объект? (Оба эти парадокса, после некоторого анализа, могут быть признаны парадоксами противоречивых посылок (англ.), либо в житейском смысле посылки будут уточнены как «непреодолимая ранее сила», воздействуя на «несдвигаемый ранее объект», даст невиданное ранее.)
• Стрела Зенона: летящая стрела каждый момент времени занимает определенное положение в пространстве. Когда же она перемещается из одного положения в другое?
• Дихотомия: «Вы никогда не попадёте из точки А в точку Б, так как вы должны будете пройти половину пути, потом половину оставшейся половины, и так бесконечное число раз».

См. также: Category:Economics paradoxes (англ.)

• Парадокс Алле: изменение возможного дохода, который разделён между несколькими альтернативами, влияет на выбор людей между этими альтернативами, что противоречит теории ожидаемой полезности.
• Парадокс Базермана^[1].
• Парадокс бережливости: если каждый будет экономить деньги во время экономического спада, то совокупный спрос упадёт и в результате уменьшатся суммарные накопления населения.
• Парадокс Бертрана — ситуация, когда два олигополиста, конкурируя между собой и достигнув равновесия Нэша, оказываются с нулевой прибылью.
• Парадокс Гибсона (англ.): почему процентные ставки и цены скоррелированы?
• Парадокс Коперника — Грешема: плохие деньги вытесняют хорошие, если они имеют одинаковую цену.
• Парадокс Гиффена: если цены на хлеб начнут повышаться, люди станут покупать его больше.
• Парадокс Джевонса: повышение эффективности ведёт к ещё бо́льшему повышению спроса.
• Парадокс Кондорсе — парадокс теории общественного выбора: правило простого большинства не в состоянии обеспечить транзитивность бинарного отношения общественного предпочтения среди выбираемых вариантов. В силу нетранзитивности результат может зависеть от порядка голосования, что даёт возможность манипуляции выбором большинства. Обобщён теоремой «о невозможности» Эрроу в 1951 г.
• Парадокс Леонтьева: некоторые страны экспортируют трудозатратные товары, а импортируют капиталозатратные, что является контрпримером к теории Хекшера — Олина.
• Парадокс продуктивности (англ.): продуктивность работника уменьшается, несмотря на улучшения в технологиях.
• Парадокс Триффина: для формирования долларовых резервов других стран необходимо, чтобы в США постоянно наблюдался дефицит платёжного баланса. Но дефицит платёжного баланса подрывает доверие к доллару и снижает его ценность в качестве резервного актива.
• Парадокс ценности: почему вода стоит дешевле алмазов, хотя потребность человека в ней гораздо больше, чем в алмазах?
• Парадокс Эджворта (англ.): может не существовать равновесия, если мощности производств ограничены.
• Парадокс Элсберга (англ.): люди предпочитают известный, хотя и бо́льший, риск неизвестному риску, что противоречит теории ожидаемой полезности.
• Информационный парадокс Эрроу^[en]: потенциальный потребитель хочет знать о приобретаемом товаре/услуге как можно больше достоверной информации, продавец же, владеющий интеллектуальной собственностью, не хочет безвозмездно раскрывать характеристики товара, и поэтому склонен обманывать покупателя, который в этом случае вынужден принимать решение на основе недостоверной иноформации.

• Парадокс неподсудного договора: если существует процессуальное правило о том, что судья, рассматривающий дело, не должен быть заинтересован в исходе его рассмотрения, то дело, имеющее в себе договор, содержащий следующее условие: «Каждый судья, который будет рассматривать дело, в котором этот договор является доказательством, в случае признания его ничтожным имеет право получить от каждой из его сторон по 1 копейке», не может быть рассмотрено никаким судьёй.

Психофизиологические[править]

Список парадоксів — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Це список парадоксів, згрупованих за темами.

Парадо́кс (від дав.-гр. παράδοξος — несподіваний, дивний) — твердження, яке на перший погляд суперечить саме собі, але може бути вірним. Слід розрізняти парадокс і апорію, яка є логічно вірною, але не може існувати в реальності. Деякі логічні парадокси використовуються для розвитку критичного мислення.

Існують не тільки логічні парадокси. Прикладом філософського парадоксу є парадокс Тесея (який запитує, чи корабель, який лагодять і заміняють кожну його частину на нову, залишається тим самим кораблем). Відомі візуальні парадокси нідерландського художника Мауріца Ешера, на картинах якого зображені сходи, які піднімаються безкінечно, або стіни, які з інших точок зору є підлогами.

• Що Черепаха сказала Ахіллові. Відомий також як парадокс Льюїса Керрола, не плутати з однойменним фізичним парадоксом.
• Пастка-22: Ситуація коли хтось потребує чогось, що може бути отримано тільки без потреби.
• Парадокс імплікації: несумісні посилання роблять аргумент правильним.
• Парадокс воронів (або ворони Хемпеля): існування червоного яблука збільшує ймовірність того, що всі ворони чорні.
• Доведення однобарвності всіх коней^[en] методом математичної індукції.
• Парадокс раптової страти: якщо сказати засудженому до страти, що вона відбудеться в несподіваний для нього день цього тижня, то він логічно прийде до висновку, що вона не може відбутися ні в один з днів тижня. Тоді вона і буде сюрпризом.
• Принцип вибуху. Вихідні положення, що протирічать, роблять валідним будь-який аргумент.
• Парадокс сатанинської пляшки Стівенсона^[en] описується схожою логікою.
• Парадокс п’яниці^[en]: в будь-якому непорожньому закладі завжди існує людина, про яку можна сказати, що якщо вона п’є, то п’ють і всі інші відвідувачі.
• Парадокс лотереї^[en]: цілком очікувано, що цей конкретний квиток не виграє, адже вірогідність його виграшу дуже мала. Але не можна очікувати, що жоден квиток не виграє.

Парадокси автореференції[ред. | ред. код]

Це добре відомий (і добре вивчений) клас протиріч, що виникають у висловлюваннях, які містять визначення чогось, що неявно посилається саме на себе.

• Парадокс голяра^[en]. Голяр голить всіх, хто не голиться сам. Чи голить він самого себе?
• Парадокс Беррі: фраза «найменше число, яке неможливо описати менш ніж десятьма словами» описує це число дев’ятьма словами.
• Парадокс Каррі: «Якщо це твердження вірне, то русалки існують».
• Парадокс крокодила: Крокодил вкрав дитину і обіцяв матері її віддати, якщо вона відповість правильно, чи віддасть крокодил їй дитину?
• Парадокс Епіменіда: крітянин каже: «Всі крітяни — брехуни».
• Парадокс брехуна: «Ця пропозиція хибна».
• Парадокс Ґреллінґа — Нельсона: Чи є слово «гетерологічний», що означає «Непридатний до самого себе», гетерологічним словом? (Близький до Парадокса Рассела.)
• Парадокс Гегеля: «Історія вчить людину тому, що людина нічому не вчиться з історії».
• Y-комбінатор в лямбда-численні та комбінаторній логіці був названий парадоксальним комбінатором оскільки він пов’язаний з самовідносністю.
• Парадокс Петронія: «Обмежуйте себе у всіх речах, навіть в обмеженні».
• Парадокс Квіна^[en]: «… тягне за собою хибність, бувши доданим до власного цитування» тягне за собою хибність, бувши доданим до власного цитування.
• «Парадокс Еватла» (софізм Еватла) : Протагор взяв учня Еватла за умови, що той йому заплатить, коли виграє першу справу. Трапилося так, що Протагор подав позов на Еватла за те, що той йому довго не платить. Чи повинен Еватл заплатити, якщо він виграє цю справу?
• Парадокс Рассела: чи містить множина всіх множин, які не містять себе, саму себе? Рассел популяризував його у формі «Парадокса цирульника»: «Цирульник голить лише тих людей, які не голять себе самі. Чи голить він себе?»
• Парадокс Рішара^[en]: якщо зіставити всі властивості чисел з числами, то можна визначити таку властивість, якій не відповідатиме жодне число.
• Парадокс всемогутності: чи може всемогутня істота створити камінь, який вона сама не зможе підняти?

Парадокси визначень[ред. | ред. код]

• Корабель Тесея: якщо кожний елемент корабля замінили хоча б один раз, чи можна вважати корабель тим самим кораблем?
• Парадокс купи. В який момент купа перестане бути купою, якщо віднімати від неї по одній піщині?
• Парадокс лисого^[ru]: якщо волосся з голови випадає по одній волосині, з якого моменту людина стає лисою?
• Парадокс цікавих чисел^[en]: найменше нецікаве натуральне число є цікавим саме по собі завдяки цьому факту, але тоді воно не відноситься до нецікавих.

Математичні та статистичні[ред. | ред. код]

• Парадокси пропорційного представництва: деякі системи представництва можуть мати наслідки, що йдуть проти інтуїції:
• Парадокс голосування (Парадокс Ерроу): не можна поєднати всі вимоги до виборчої системи в одній системі.
• Закон Бенфорда: в багатьох списках чисел з довільних реальних джерел більшість чисел починаються з цифри 1.
• Парадокс ліфта: ліфти найчастіше ходять в одному напрямку — від середини будівлі вниз до підвалу та вгору до горища
• Парадокс очікування: чому іноді доводиться чекати на автобус довше, ніж потрібно. (пояснення дивіться в статті теорія відновлення)
• гра в нетранзитивні кубики: існує набір з 3 гральних кубиків А, В і С таких, що найчастіше на А випадає більше число, ніж на В; на В частіше випадає більше число, ніж на С; на С частіше випадає більше число, ніж на А.
• Гра Пенні^[en]: нетранзитивний парадокс, різновид гри в нетранзитивні кубики.
• Парадокс Ліндлі: маленькі помилки в нульовій гіпотезі сильно зростають, якщо аналізуються великі масиви даних, приводячи до помилкових, але одночасно точних зі статистичної точки зору результатів.
• Парадокс недоношеності^[en]: низька вага при народженні та куріння матері призводять до великої смертності. Діти курців мають нижчу вагу при народженні, однак низьковагові діти курців мають нижчу смертність, ніж інші низьковагові діти.
• Парадокс зниклого долара^[en]: неправильна логіка призводить до того, що один долар «пропадає».
• Парадокс кореляції: цілком можливо зробити помилкові висновки з кореляції. Наприклад, міста з великою кількістю церков мають більше злочинів, оскільки обидва чинники випливають з більшого населення. Це називається удаваною кореляцією.
• Тріада негативних кореляцій в парадоксі голосування (Парадокс Кондорсе/Arrow ‘s paradox(англ.)): виборець 1 ранжирує трьох кандидатів в порядку А, В, С; виборець 2 — в порядку В, С, А; виборець 3 — в порядку С, А, В. Таким чином, будь-які дві третини виборців згодні між собою в порівняльній оцінці двох третин кандидатів.
• Феномен Уілла Роджерса^[en]: математичне поняття середнього, визначене як середнє арифметичне або медіана (неважливо), призводить до парадоксального результату — наприклад, можна перемістити статтю з Вікіпедії в Вікіцитати так, щоб середня довжина статті збільшилася на обох сайтах!
• Парадокс маляра: нескінченну за площею платівку можна зафарбувати кінцевою кількістю фарби.
• Парадокс Паррондо: можливо виграти, граючи за чергою в дві наперед програшні ігри.
• Парадокс ряду 1-1 + 1-… (Ряд Гранді): наявний нескінченний ряд 1-1 + 1-… Чому він дорівнює? Можна довести, що він дорівнює 0, 1 або 0,5.
• Як не парадоксально, але при достатньо природних визначеннях можна показати, що 1 + 2 + 3 + 4 +… =-1/12.

Ймовірнісні[ред. | ред. код]

• Парадокс Берксона^[en]: дві незалежних події стають умовно залежними за умови, що хоча б одна з них відбулася.
• Парадокс Бертрана: різні визначення випадкової величини, засновані на «здоровому глузді», дають різні результати.
• Парадокс днів народження: яка імовірність того, що у двох учнів з одного класу день народження збігається? Виявляється — більш ніж 50%, якщо учнів більш ніж 23.

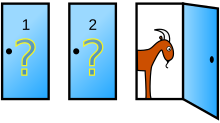Загадка Монті Холла: в пошуках автомобіля гравець вибирає двері 1. Тоді ведучий відкриває треті двері, за якими розташована коза, і пропонує гравцеві змінити свій вибір на двері 2. Чи збільшуються шанси гравця при виборі дверей 2?

• Парадокс Бореля^[en]: густина умовної ймовірності не інваріантна при перетвореннях координат.
• Стать другої дитини: якщо один з двох дітей у родині — хлопчик, яка ймовірність того, що друга дитина — дівчинка?
• Парадокс Монті Голла: неочевидний наслідок умовної ймовірності. Власне те саме, що і задача трьох в’язнів^[en].
• Парадокс Сімпсона: основні інтереси підсуспільства можуть виявитися зовсім не основними для всього суспільства. Тому якщо два ряди даних відповідають одній певній гіпотезі, бувши об’єднаними, вони можуть відповідати протилежній гіпотезі.
• Задача сплячої красуні: ймовірнісна задача, яка може мати як відповідь 1/2 або 1/3 в залежності від того, з якого боку розглядати питання.
• Задача трьох карток^[en]: істинна ймовірність того, що зворотній бік випадково вибраної карти виявиться того ж кольору, що й верхній, суперечить інтуїтивній оцінці такої ймовірності деякими людьми.
• Парадокс двох конвертів: вам дають два однакових конверти і кажуть, що один з них містить в два рази більше грошей, ніж інший. Ви повинні відкрити один з них, перевірити вміст, а потім, не відкриваючи іншого, вирішити, який з конвертів узяти.
• Парадокс парі^[ru]: в деяких ситуаціях вигідно сперечатися обом супротивникам, бо обидва мають більші шанси на перемогу, ніж на програш.
• Омана гравця — (помилковий висновок Монте-Карло) про те, що вигідно ставити на червоне, якщо чорне випало 10 разів підряд.
• Санкт-петербурзький парадокс: люди навряд чи будуть грати в цю гру, хоча математичне сподівання виграшу в ній нескінченно велике.
• Парадокс закономірності^[ru]: побачивши явну закономірність у результатах серії випробувань (наприклад, випадання 10 000 разів підряд одного і того самого варіанта з двох можливих), ми будемо схильні вважати, що випробування не є випадковими. Однак поява будь іншій послідовності з 10 000 значень у випадкових випробуваннях є настільки ж малоймовірною подією.

Пов’язані з нескінченністю[ред. | ред. код]

Геометричні або топологічні[ред. | ред. код]

• Парадокс Банаха — Тарського: можна розрізати кулю на 5 частин, скласти їх по-іншому і вийде дві кулі такого самого радіуса, як у початкової.
• Квадратура круга Тарського: круг і квадрат рівної площі рівноскладені при кінцевому розбитті.
• Ріг Гавриїла або «труба Торрічеллі»: просте тіло, що має кінцевий об’єм, але нескінченну площу поверхні. Множина Мандельброта та різні інші фрактали мають кінцеву площу, але нескінченний периметр. Більш того на межі множини Мандельброта не існує двох різних точок, між якими відстань по периметру була б кінцевою, що можна зрозуміти так: якщо Ви підете вздовж межі цієї множини, Ви анітрохи не зрушите з однієї точки.
• Парадокс Хаусдорфа: існує зліченна підмножина C на сфері S така, що S \\ C можна розбити на дві копії самого себе.
• Парадокс узбережжя: периметр континенту не може бути коректно визначеним (не може бути зіставленим з конкретним числом)

Парадокс Смейла стверджує, що можна вивернути (з самоперетинами, але без складок) сферу в тривимірному просторі. Одна з проміжних конфігурацій, Поверхні Моріна^[en], представлена на малюнку.

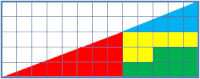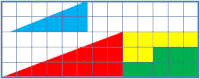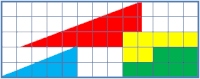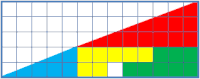
• Парадокс Смейла: сфера топологічно може бути вивернута навиворіт.
• Зникнення клітини: при різних варіанти складання одних і тих самих елементів в однакову фігуру. «Зникнення» елемента наочно демонструє, що площі одержуваних фігур різні. (При більш уважному розгляді, однак, можна помітити, що вихідна та кінцева фігури різні, цим і пояснюється різниця площ, тому цей парадокс відноситься до візуальних ілюзій.)

• Парадокс Абіліна: буває, що люди приймають рішення, засновані не на тому, що вони самі хочуть, але на тому, що вони думають, що інші хочуть. У результаті виходить, що кожний робить щось, що нікому насправді не потрібно.
• Буриданів осел: як можна зробити раціональний вибір між двома речами, що мають однакову цінність?
• Вилка Мортона: вибір з двох поганих альтернатив («вибір з двох зол»).
• Загадка Кавки про отруту^[en]: чи може людина мати намір випити смертельну отруту, якщо наявність наміру — єдина річ, яка потрібна для отримання нагороди?
• Дилема в’язня: за деяких умов оптимальна стратегія поведінки кожного гравця, якщо кожний гравець виходить з егоїстичних міркувань, виявляється програшною для групи в цілому і для кожного гравця окремо.

З теорії відносності та квантової механіки[ред. | ред. код]

• Парадокс Белла: чи розірветься струна, що з’єднує релятивістські об’єкти?
• Парадокс Ейнштейна — Подольського — Розена: чи можуть віддалені події впливати одна на одну (в квантовій механіці)?
• ГЗК-парадокс^[en]: спостережувані високоенергетичні космічні промені, схоже, порушують межу Грайзена-Зацепіна-Кузьміна^[en], яка є наслідком СТВ.
• Парадокс драбини: Чи може драбина за рахунок релятивістського скорочення довжини поміститися в менший за розміром гараж?
• Кіт Шредінгера. Квантовий парадокс: кіт живий чи мертвий перед тим, як ми на нього подивимося? Пов’язаний з ним парадокс друга Вігнера.
• Парадокс близнят: коли близнюк-мандрівник повернувся, він став молодшим або старшим, ніж його брат, який залишався на Землі?
• Парадокс субмарини: сила Архімеда на релятивістський об’єкт (типу кулі (для рушниці)) змінюється при переході від системи відліку, в якій покоїться куля, до системи відліку, в якій покоїться рідина.
• Парадокс Еренфеста про кінематику абсолютно твердого диска, що обертається.
• Зникнення інформації в чорній дірі^[en]: чорна діра порушує загальновизнану наукову догму — що інформація не знищується.

Пов’язані з подорожами в часі[ред. | ред. код]

• Парадокс походження^[en] ставить питання про походження об’єктів або інформації при подорожах у минуле.
• Парадокс убитого дідуся: ви переміщується в минуле та вбиваєте свого дідуся до того, як він познайомився з Вашою бабусею. Через це Ви не зможете з’явитися на світ і, отже, не зможете вбити свого дідуся.
• Парадокс приречення^[en]: людина потрапляє в минуле, має статевий зв’язок зі своєю прабабусею та зачинає свого дідуся. У результаті виходить низка нащадків, включаючи батька цієї людини і його самого. Отже, якби він не подорожував в минуле, його б взагалі не існувало.

Гідродинамічні[ред. | ред. код]

Термодинамічні[ред. | ред. код]

• Теплова смерть Всесвіту: 1850 року німецький фізик Р. Клаузіус «… Дійшов висновку, що в природі теплота переходить від теплого тіла до холодного… стан Всесвіту повинен все більше змінюватися в певному напрямку… Ці уявлення розвинув англійський фізик Вільям Томсон, згідно з яким всі фізичні процеси у Всесвіті супроводжуються перетворенням світлової енергії в теплоту». Отже, Всесвіт очікує «теплова смерть», тому нескінченне існування Всесвіту в часі неможливе.
• Парадокс теплообміну: дві однакові маси води мають різну температуру. Чи можна шляхом теплообміну нагріти більш холодну воду до вищої температури, ніж кінцева температура охолоджувальної води? Адже як відомо, тепло може переходити лише від більш нагрітого тіла до більш холодного.
• Парадокс Гіббса: чи є в ідеальному газі Ентропія екстенсивною (аддитивною) змінною?
• Парадокс Лошмідта^[en]: чому зростання ентропії є неминучим, хоча фізичні закони інваріантні щодо інверсії часу?
• Парадокс перемішування — щодо ентропії системи до і після перемішування.
• Парадокс Мпемби: гаряча вода (за деяких умов) може замерзнути швидше, ніж холодна. Хоча при цьому вона повинна пройти через температуру холодної води в процесі замерзання.
• Демон Максвелла: При змішуванні холодного з гарячим холодне стане холоднішим, а гаряче додатково нагріється.

Космологічні парадокси[ред. | ред. код]

Інші[ред. | ред. код]

• Корпускулярно-хвильовий дуалізм — світло може розглядатися або як електромагнітна хвиля, швидкість розповсюдження в вакуумі якої постійна, або як потік фотонів — частинок, що володіють певною енергією, імпульсом, власним моментом імпульсу та нульовою масою.
• Парадокс Бреса: пристрій, що збільшує потужність мережі, може зменшити загальну продуктивність.
• Парадокс Керрола^[en]: момент інерції палички повинен бути рівним нулю, але він не дорівнює.
• Парадокс Денні^[ru]: членистоногі які живуть на поверхні води, згідно з розрахунками, не можуть рухатися по поверхні, адже це суперечить природі.
• Парадокс інтернету: ймовірність існування потрібної інформації в Інтернеті зростає, а можливість її знайти зменшується.
• Апорія Зенона «Ахіллес і черепаха»: прудконогий Ахіллес ніколи не наздожене неквапливу черепаху, якщо на початку руху черепаха була попереду Ахіллеса, оскільки доки він переміститься в точку, де була черепаха, вона встигне просунутися хоч трохи вперед.
• Парадокс спостерігача пов’язаний із ситуацією, коли феномен, що піддається спостереженню, мимоволі підпадає під вплив через сам факт присутності спостерігача.

• Проблема курки та яйця: що було раніше — курка чи яйце? З одного боку, для появи курки необхідне яйце, з іншого — для появи яйця потрібна курка.
• Тотальна кара, або парадокс смертної кари: вбивство в деяких країнах карається стратою. Але виконуючи вирок, держава (тобто всі його жителі) стають вбивцями та повинні бути засуджені до смерті.
• Парадокс епікурейців, або Проблема зла: здається, що існування зла несумісне з існуванням всемогутнього та дбайливого Бога.
• Парадокс Ньюкома — парадокси всезнання:
  • Чому можна виграти у суперника, який знає все?
• Парадокс Хаттона^[en]: якщо хтось запитує себе: «Чи я сплю?», то це доводить, що він спить, то що це доводить під час неспання?
• Парадокс ліберальності^[en]: «мінімальна свобода» не є рівноважною згідно з Парето.
• Адитивність щастя^[en]: що краще: велика група людей, яка живе стерпним життям, або невелика, що живе щасливо?
• Парадокс Мура^[en]: «Йде дощ, але я не вірю в це».
• Парадокс нігілізму^[en]: якщо правди не існує, то твердження «правди не існує» правдиве, що доводить його неправдивість.
• Парадокс всемогутності: чи може всемогутня істота створити камінь, який вона сама не зможе підняти?
• Достатньо близький до попереднього Парадокс непереборної сили^[en]: що буде, якщо непереборна сила подіє на непорушний об’єкт? (Обидва ці парадокси, після деякого аналізу, можуть бути визнані парадоксами суперечливих посилань, або в життєвому сенсі посилки будуть уточнені як «непереборна раніше сила», впливаючи на «непорушний раніше об’єкт», дасть небачене раніше.)
• Стріла Зенона: стріла під час польоту в кожний момент часу займає певне положення в просторі. Коли ж вона переміщується з одного положення в інше?
• Дихотомія: «Ви ніколи не потрапите з точки А в точку Б, оскільки ви повинні будете пройти половину шляху, потім половину того що залишився, і так нескінченне число разів».

• Парадокс Аллі: зміна можливого прибутку, розподіленого між декількома альтернативами, впливає на вибір людей між цими альтернативами, що суперечить теорії очікуваної користі.
• Парадокс Базермана^[2].
• Парадокс ощадливості: якщо кожний буде економити гроші під час економічного спаду, то сукупний попит впаде і внаслідок зменшаться сумарні накопичення населення.
• Парадокс Бертрана — ситуація, коли два олігополісти, конкуруючи між собою та досягнувши рівноваги Неша, опиняються з нульовим прибутком.
• Парадокс Гібсона^[en]: чому процентні ставки і ціни скорельовані?
• Парадокс Коперника — Грешема: погані гроші витісняють хороші, якщо вони мають однакову ціну.
• Парадокс Гіффена: якщо ціни на хліб почнуть підвищуватися, люди стануть купувати його більше.
• Парадокс Джевонса: підвищення ефективності веде до ще більшого підвищення попиту.
• Парадокс Кондорсе — парадокс теорії суспільного вибору: правило простої більшості не в змозі забезпечити транзитивність бінарного відношення громадського переваги серед обираних варіантів. В силу нетранзитивності^[en] результат може залежати від порядку голосування, що дає можливість маніпуляції вибором більшості. Узагальнене теоремою «про неможливість» Ерроу 1951 р

парадокс — Paradox — qwe.wiki

Парадокс является утверждением , что, несмотря на по- видимому , действительное рассуждение из истинных посылок, приводит к , по- видимому, противоречивым или логически недопустимому заключению. Парадокс включает противоречивые-но-взаимосвязанные элементы , которые существуют одновременно , и сохраняются в течение долгого времени.

Некоторые логические парадоксы , как известно, недопустимые аргументы , но по — прежнему ценны в развитии критического мышления .

Некоторые парадоксы выявили ошибки в определениях , принятых быть строгими, и вызвали аксиомы математики и логики , которые будут пересмотрены. Одним из примеров является парадокс Рассела , который сомневается в том , «список всех списков , которые не содержат себя» будет включать себя, и показал , что попытки основать теории множеств на идентификации множеств с свойств или предикатами были ошибочными. Другие, такие как парадокс Карри , пока не решен.

Примеры вне логики включают корабль Тесея от философии (сомнение ли отремонтировать корабль с течением времени путем замены каждого и всех ее деревянных частей, по одному за раз, будет оставаться таким же корабль). Парадоксы могут также принимать форму изображений или других средств массовой информации. Например, Эшер признаки перспективных на основе парадоксов во многих из его рисунков, со стенами, которые рассматриваются как полы из других точек зрения, и лестничные клетками , которые появляются , чтобы подняться до бесконечности.

В обиходе слово «парадокс» часто ссылается на заявления , которые могут быть и истинным и ложным то ироническое или неожиданное, например , как «парадокс , что стоя является более утомительно , чем ходить».

логический парадокс

Общие темы в парадоксах включают самореференцию , бесконечный регресс , круговые определения и путаницу между различными уровнями абстракции .

Патрик Хьюз выделяет три законы парадокса:

Самоссылки

Примером может служить «Это утверждение ложно», это форма лжец парадокс . Оператор имеет в виду себя. Другим примером самоссылки является вопрос о том, является ли цирюльник бреет себя в парикмахерской парадокс . Еще одним примером может быть «ответ на этот вопрос„Нет“?»

Противоречие

«Это утверждение ложно»; утверждение не может быть ложным и истинным в то же время. Другой пример противоречия, если человек разговаривает с джином желает, чтобы желания не суждено было сбыться. Это противоречит самой себе, потому что, если джин предоставляет свое желание, он не удовлетворил его желание, и если он отказывается удовлетворить его желание, то он действительно удовлетворить его желание, поэтому делает его невозможно ни предоставлять или не предоставлять его желание, потому что его желание противоречит самому себе.

Vicious округлость, или бесконечный регресс

«Это утверждение ложно»; если утверждение верно, то утверждение ложно, что делает утверждение верно. Другой примером порочной округлости является следующей группой операторов:

«Следующее предложение истинно.»

«Предыдущее предложение ложно.»

Другие парадоксы связаны ложные высказывания ( «„невозможно“не слово в моем словаре», простой парадокс) или полуправды и полученные в результате предвзятых предположений. Эта форма распространена в перлов .

Например, рассмотрим ситуацию , в которой отец и сын его водите вниз по дороге. Автомобиль врезался в дерево и погибает отец. Мальчик доставлен в ближайшую больницу , где он готовится к экстренной операции . При входе в хирургии люкса, хирург говорит, «Я не могу работать на этом мальчике. Он мой сын.»

Кажущийся парадокс обусловлен поспешным обобщением , ибо если хирург отец мальчика, заявление не может быть правдой. Парадокс разрешается , если выясняется , что хирург мать женщины-мальчика.

Парадоксы , которые не основаны на скрытую ошибке обычно возникают на периферии контекста или языка , и требуют расширения контекста или языка для того , чтобы потерять их парадоксальное качество. Парадоксы , которые возникают из — видимому , вразумительных использования языка часто представляет интерес для логиков и философов . «Это предложение ложно» является примером хорошо известного лжеца парадокс : это предложение , которое не может быть последовательно интерпретировать как истинным или ложным, потому что если он , как известно, ложно, то известно , что оно должно быть истинным , и если известно , чтобы быть правдой, то известно , что оно должно быть ложным. Парадокс Рассела , который показывает , что понятие о множестве всех тех множеств , которые не содержат себя приводит к противоречию, сыграл важную роль в развитии современной логики и теории множеств.

Мысле-эксперименты могут дать интересные парадоксы. Дед парадокс , например, мог бы возникнуть , если время путешественник был убить свой собственный дед , прежде чем его мать или отец была задумана, тем самым предотвращая его собственное рождение. Это конкретный пример более общего наблюдения эффекта бабочки , или что взаимодействие путешественником во времени с прошлым, однако незначительное, повлечет за собой внесение изменений , которые, в свою очередь, изменить будущее , в котором путешествие во времени еще произойти, и, таким образом , изменить обстоятельства самого путешествия во времени.

Часто, казалось бы, парадоксальный вывод вытекает из противоречивого или по своей сути противоречивого определения исходной посылки. В случае такого очевидного парадокса времени путешественник убивает свой собственный дедушка, это несоответствие определения прошлого к которому он возвращается как-то отличается от того, которая приводит к будущему, с которого он начинает свою поездку, но также настаивает на том, что он должен прийти к этому прошлому из того же будущего, как тот, что ведет к.

Классификация Куайна

WV Куайн (1962) различие между тремя классами парадоксов:

• Правдивый парадокс дает результат , который появляется абсурдным , но демонстрируется , чтобы быть правдой , тем не менее. Таким образом, парадокс дня рождения Фредерика в Пираты Пензанс устанавливает тот удивительный факт , что двадцать один-летний имели бы только пять дней рождения , если он родился на високосный день . Кроме того, теорема Эрроу демонстрирует трудности в результатах голосования картографирования к воле народа. Парадокс Монти Холла показывает , что решение , которое имеет интуитивный 50-50 шанс на самом деле сильно смещена в сторону принятия решения , которое, учитывая интуитивное заключение, игрок будет вряд ли сделает. В науке двадцатого века, парадокс Гильберта о Grand Hotel и кошке Шредингера является лихом ярких примеров теории принимаются до логического конца , но парадоксального.
• Falsidical парадокс устанавливает результат , который не только появляется ложным , но на самом деле это неверно, из — за ошибочности в демонстрации. Различные недопустимые математические доказательства (например, что 1 = 2) являются классическими примерами, как правило , полагаются на скрытом деление на ноль . Другой примером является индуктивной формой лошади парадокса , который ложно обобщающим от истинных конкретных утверждений. Парадоксы Зенона являются «falsidical», заключая, например, что летящая стрела никогда не достигает своей цели , или что быстрый бегун не может догнать черепаху с небольшой головной старт.
• Парадокс , который ни в одном классе может быть антиномия , которая достигает противоречивую результат, правильно применяя принятые способы рассуждения. Например, парадокс Греллингом-Нельсон указывает подлинные проблемы в нашем понимании идеи истины и описания.

Четвертый вид иногда описывается так работы Куайна.

• Парадокс , который является одновременно истинным и ложным в то же время и в том же смысле , что называется dialetheia . В западных логик часто предполагается, следуя Аристотелю , что никакие dialetheia не существуют, но они иногда принимаются в восточных традициях (например , в моисты , в Gongsun Longzi , и в дзен ) и в паранепротиворечивых логик . Было бы просто двусмысленность или вопрос степени, к примеру, как утверждает , и отрицать , что «Джон здесь» , когда Джон находится на полпути через дверь , но она внутренне противоречиво одновременно утверждать и отрицать это событие.

В философии

Вкус к парадоксу занимает центральное место в философии Лаоцзы , Чжуан — цзы , Гераклита , Бхартрихари , Мейстер Экхарт , Гегель , Кьеркегор , Ницше и Г. К. Честертон , среди многих других. Серен Кьеркегор, например, пишет в философских фрагментов , которые

Но не надо думать плохо о парадоксе, ибо парадокс заключается страсть мысли, и мыслитель, не парадокс, как любовник без страсти: посредственного парень. Но в конечном итоге потенцирование всякой страсти всегда хотение свое собственное падение, и так же в конечном итоге страсть понимания того, будет столкновение, хотя в той или иной мере столкновения должно стать его падение. Это, то, в конечном итоге парадокс мысли: хочу, чтобы обнаружить то, что сама мысль не может думать.

В медицине

Парадоксальная реакция на препарат является противоположностью того , что можно было бы ожидать, например, становится волнуемым успокоительным или седативным по стимулятору . Некоторые из них являются общими и регулярно используются в медицине, например, использование стимуляторов , таких как Adderall и Риталин в лечении синдрома дефицита внимания с гиперактивностью (также известный как СДВГ) , а другие являются редкими и могут быть опасны , поскольку они не ожидали, такие как тяжелое волнении от бензодиазепинов .

Смотрите также

Рекомендации

Заметки

Список используемой литературы

• Марк Sainsbury, 1988, парадоксы, Кембридж: Cambridge University Press
• Уильям Poundstone, 1989, Лабиринты разума: Paradox, головоломки, и Frailty знаний, Якорь
• Рой Соренсен, 2005, Краткая история парадокса: Философия и Лабиринты разума, Oxford University Press
• Патрик Хьюз , 2011, Paradoxymoron: Глупая Мудрость в словах и картинках, Reverspective

внешняя ссылка

Wikiquote имеет цитаты , связанные с: Paradox

Посмотрите парадокс в Викисловарь, бесплатный словарь.

Этот звуковой файл был создан с пересмотром статьи « Paradox » от 2005-07-07, и не отражать последующие изменения к статье. ( Аудио помощь )

Список парадоксов — Википедия переиздана // WIKI 2

Это список парадоксов , сгруппированных по тематике. Группировка является приблизительной, поскольку парадоксы могут относиться более чем к одной категории. В этом списке собраны только сценарии, которые были названы парадоксом по крайней мере одним источником и имеют свою собственную статью в Википедии. Хотя они считаются парадоксами, некоторые из них просто основаны на ложных рассуждениях (фальсифицированных) или не интуитивном решении (достоверно).Неформально термин парадокс часто используется для описания противоречащего интуиции результата.

Однако некоторые из этих парадоксов подходят для того, чтобы соответствовать общепринятому восприятию парадокса, что является противоречивым результатом, полученным даже при правильном применении общепринятых способов рассуждения. Эти парадоксы, часто называемые антиномией, , указывают на подлинные проблемы в нашем понимании идей истины и описания.

Энциклопедия YouTube

• 1/5

  Просмотры:

  528125

  3 343 386

  12 886 854

  8 965 307

  3 684 698

• ✪ 25 САМЫХ БЕЗУМНЫХ парадоксов, поразивших вас

• ✪ 3 парадокса путешествий во времени !!

• ✪ Парадокс Ферми — Где все пришельцы? (1/2)

• ✪ Бесконечный парадокс отеля — Джефф Декофски

• ✪ Разъяснение парадокса береговой линии

Содержание

Логика

• Парадокс парикмахерской : Предположение о том, что «если одно из двух одновременных предположений приводит к противоречию, другое предположение также опровергается» приводит к парадоксальным последствиям.Не следует путать с парадоксом Барбера.
• Что Черепаха сказала Ахиллу : Если нужно сделать предположение, что конкретный результат может быть выведен из предпосылок, то результат никогда не может быть выведен. Также известен как парадокс Кэрролла , и его не следует путать с парадоксом «Ахилл и черепаха» Зенона Элейского.
• Catch-22 : Ситуация, в которой кто-то нуждается в чем-то, что можно получить, только если в этом не нуждаются.Солдат, который хочет, чтобы его объявили сумасшедшим, чтобы избежать боя, не считается сумасшедшим именно по этой причине и, следовательно, не будет объявлен сумасшедшим.
• Парадокс пьющего : В любом пабе есть такой покупатель, что если он пьет, то пьют все в пабе.
• Парадокс следствия : Несогласованные посылки всегда делают аргумент действительным.
• Парадокс лотереи : Если есть один выигрышный билет в большой лотерее, разумно полагать, что любой конкретный лотерейный билет не является выигрышным, но неразумно полагать, что ни один лотерейный билет не выиграет.
• Парадокс ворона : (или Вороны Хемпеля): наблюдение за зеленым яблоком увеличивает вероятность того, что все вороны будут черными.
• Парадокс Росса : Введение дизъюнкции создает проблему для императивного вывода, по-видимому, позволяя вывести произвольные императивы.
• Неожиданный парадокс повешения : День повешения будет сюрпризом, поэтому этого не может быть вообще, поэтому это будет сюрприз. Неожиданная проверка и парадокс бутылочного беса используют аналогичную логику.

Самостоятельная ссылка

Эти парадоксы имеют общее противоречие, возникающее либо из-за ссылки на себя, либо из-за циклической ссылки, в которой несколько утверждений относятся друг к другу таким образом, что следование некоторым ссылкам приводит к исходной точке.

• Парадокс парикмахера : парикмахер бреет всех и только тех мужчин, которые не бреют себя. Он бреется? (Популяризация Расселом его теоретико-множественного парадокса.)
• Парадокс Бхартрахари : Тезис о том, что есть некоторые вещи, которые не могут быть названы, противоречит представлению о том, что что-то называется безымянным.
• Ягодный парадокс : Фраза «первое число, которое нельзя назвать менее чем десятью словами», кажется, обозначает его девятью словами.
• Дилемма крокодила : Если крокодил крадет ребенка и обещает его вернуть, если отец может правильно угадать, что именно сделает крокодил, как крокодил должен отреагировать в случае, если отец догадывается, что ребенок не будет возвращен?
• Парадокс суда : Студент юридического факультета соглашается заплатить своему учителю после (и только после) победы в его первом деле.Затем учитель предъявляет иск ученику (который еще не выиграл дело) о выплате.
• Парадокс Карри : «Если это предложение верно, то Санта-Клаус существует».
• Парадокс Эпименида : Критянин говорит: «Все критяне лжецы». Этот парадокс работает в основном так же, как парадокс лжеца.
• Парадокс Греллинга-Нельсона : Является ли слово «гетерологический», означающее «неприменимый к самому себе», гетерологическим словом? (Близкий родственник парадокса Рассела.)
• Парадокс Гильберта-Бернейса : Если бы существовало имя для натурального числа, идентичное имени преемника этого числа, было бы натуральное число, равное его преемнику.
• Парадокс Клини – Россера : Формулировка эквивалента парадокса Ричарда показывает, что нетипизированное лямбда-исчисление непоследовательно.
• Парадокс знающего : «Это предложение неизвестно».
• Парадокс лжецов : «Это предложение неверно.«Это канонический парадокс самореференции. Также« Ответ на этот вопрос «нет»? »И« Я лгу ».
  • Парадокс карты : «Следующее утверждение верно. Предыдущее утверждение неверно». Вариант парадокса лжеца, в котором ни одно из предложений не использует (прямую) ссылку на себя, вместо этого это случай круговой ссылки.
  • Парадокс нет-нет : Два предложения, каждое из которых утверждает, что другое не соответствует действительности.
  • Парадокс Пиноккио : Что было бы, если бы Пиноккио сказал: «Мой нос теперь растет»? ^[1]
  • Парадокс Куайна : «При добавлении к его собственной цитате появляется ложь», когда добавляется к его собственной цитате, получается ложь.»Показывает, что предложение может быть парадоксальным, даже если оно не ссылается на самого себя и не использует указательные или указательные элементы.
  • Парадокс Ябло : Упорядоченная бесконечная последовательность предложений, каждое из которых говорит, что все последующие предложения ложны. Несмотря на то, что он построен таким образом, чтобы избегать ссылок на себя, нет единого мнения о том, полагается ли он на ссылки на себя или нет.
• Противоположный день : «Сегодня противоположный день». Следовательно, это не противоположный день, но если вы скажете, что это нормальный день, он будет считаться нормальным днем, что противоречит тому факту, что ранее было указано, что это противоположный день.
• Парадокс Ричарда : Похоже, мы можем использовать простой английский язык для определения десятичного разложения таким образом, чтобы это противоречило самому себе.
• Парадокс Рассела : Содержит ли набор всех тех множеств, которые не содержат самих себя?
• Парадокс Сократа : «Все, что я знаю, это то, что я ничего не знаю».

Неопределенность

• Корабль Тесея : Кажется, что можно заменить любой компонент корабля, и это все тот же корабль.Таким образом, они могут заменять их все по одному, и это все тот же корабль. Однако затем они могут взять все оригинальные части и собрать из них корабль. Это тоже тот же корабль, с которого они начали.

См. Также Список примеров кораблей Тесея

• Парадокс Сорита (также известный как парадокс кучи): если удалить одну песчинку из кучи, у них все равно останется куча. , Если они будут и дальше удалять отдельные зерна, кучка исчезнет.Может ли одна песчинка сделать разницу между кучей и не кучей?

Математика

• Все лошади одного цвета : Ошибочный аргумент индукции, который, кажется, доказывает, что все лошади одного цвета.
• Муравей на резиновой веревке : Муравей, ползающий по резиновой веревке, может дотянуться до конца, даже если веревка тянется намного быстрее, чем муравей может ползти.
• Парадокс Крамера : Количество точек пересечения двух кривых более высокого порядка может быть больше, чем количество произвольных точек, необходимых для определения одной такой кривой.
• Парадокс лифта : Может показаться, что лифты в основном движутся в одном направлении, как если бы они производились в центре здания и разбирались на крыше и в подвале.
• Парадокс интересных чисел : Первое число, которое можно считать «скучным», а не «интересным», становится интересным именно из-за этого.
• Картофельный парадокс : Если картофель, состоящий на 99% из воды, высыхает и на 98% состоит из воды, он теряет 50% своего веса.
• Парадокс Рассела : Содержит ли набор всех тех множеств, которые не содержат самих себя?

Статистика

• Парадокс Абельсона : Размер эффекта не может указывать на практическое значение.
• Парадокс точности : Прогностические модели с заданным уровнем точности могут иметь большую предсказательную силу, чем модели с более высокой точностью.
• Парадокс Берксона : усложняющий фактор, возникающий при статистических проверках пропорций.
• Парадокс Фридмана : Описывает проблему выбора модели, при которой переменные-предикторы, не имеющие объяснительной силы, могут казаться важными искусственно.
• Парадокс дружбы : Почти у всех друзей больше друзей, чем у них.
• Парадокс осмотра : Почему автобус ждут дольше, чем следует?
• Парадокс Линдли : Крошечные ошибки в нулевой гипотезе увеличиваются при анализе больших наборов данных, что приводит к ложным, но очень статистически значимым результатам.
• Парадокс низкой массы тела при рождении : Низкая масса тела при рождении и курящие матери способствуют более высокому уровню смертности. Младенцы курильщиков имеют более низкий средний вес при рождении, но дети с низким весом при рождении, рожденные от курильщиков, имеют более низкий уровень смертности, чем другие дети с низким весом при рождении. Это частный случай парадокса Симпсона.
• Парадокс Симпсона , или Эффект Юла – Симпсона : Тренд, который появляется в разных группах данных, исчезает при объединении этих групп, а для агрегированных данных появляется обратный тренд.
• Феномен Уилла Роджерса : Математическая концепция среднего, независимо от того, определяется ли оно как среднее или медианное, приводит к очевидно парадоксальным результатам — например, возможно, что перемещение статьи из энциклопедии в словарь увеличит среднюю длину статьи. на обе книг.

Вероятность

• Парадокс коробки Бертрана : Парадокс условной вероятности, тесно связанный с парадоксом мальчика или девочки.
• Парадокс Бертрана : Разные здравые определения случайности дают совершенно разные результаты.
• Задача о дне рождения : Какова вероятность того, что у двух человек в комнате один день рождения?
• Парадокс Бореля : Условные функции плотности вероятности не инвариантны относительно преобразований координат.
• Парадокс мальчика или девочки : В семье с двумя детьми есть хотя бы один мальчик. Какова вероятность, что у него есть девушка?
• Головоломка с дротиком: Если дротик гарантированно попадает в доску для дротика и вероятность попадания в определенную точку положительна, добавление бесконечного количества положительных шансов дает бесконечность, но вероятность попадания в мишень равна единице.Если вероятность попадания в каждую точку равна нулю, вероятность попадания в любую точку мишени равна нулю. ^[2]
• Ложноположительный парадокс : Тест, который в подавляющем большинстве случаев является точным, может показать, что у вас есть болезнь, но вероятность того, что она у вас действительно есть, все еще мала.
• Парадокс Грайса : показывает, что точное значение утверждений, включающих условные выражения и вероятности, более сложное, чем может быть очевидно при случайном рассмотрении.
• Задача Монти Холла : Неинтуитивное следствие условной вероятности.
• Парадокс галстука : Ставка между двумя людьми, кажется, выгодна им обоим. По сути, очень похоже на парадокс двух конвертов.
• Нетранзитивный кубик : у одного может быть три кубика, называемые A, B и C, так что A, вероятно, выиграет в броске против B, B, вероятно, выиграет в броске против C, и C, вероятно, выиграет в рулоне против A.
• Парадокс Пробстинга : Критерий Келли часто является оптимальной стратегией для максимизации прибыли в долгосрочной перспективе.Парадокс Пробстинга, по-видимому, показывает, что критерий Келли может привести к краху.
• Задача «Спящая красавица» : проблема вероятности, на которую можно правильно ответить как половину или одну треть в зависимости от того, как подойти к вопросу.
• Проблема с тремя картами : Когда вы вытаскиваете случайную карту, как вы определяете цвет нижней стороны?
• Задача о трех узниках : вариант задачи Монти Холла.
• Парадокс двух конвертов : Вам выдаются два неотличимых конверта, каждый из которых содержит положительную сумму денег.В одном конверте вдвое больше, чем в другом. Вы можете выбрать один конверт и оставить все, что в нем есть. Вы выбираете один конверт наугад, но перед тем, как открыть его, вы можете взять другой конверт.

Бесконечность и бесконечно малые

• Парадокс Бенардете : Судя по всему, человека можно «заставить оставаться там, где он есть, просто из-за невыполненных намерений богов».
• Парадокс мрачного жнеца : Бесконечное количество убийц может создать явное внутреннее противоречие, планируя свои убийства в определенное время.
• Серия Гранди : Сумма 1-1 + 1-1 + 1-1 … может быть единицей, нулем или половиной.
• Парадокс Росса – Литтлвуда : Сколько шаров остается после того, как поочередно добавлять и убирать шарики в вазу бесконечно часто?
• Лампа Томсона : После того, как лампа постоянно включается и выключается, включается она или выключается?

Геометрия и топология

• Парадокс Банаха – Тарского : Разрежьте шар на конечное количество частей и заново соберите части, чтобы получить два шара, каждый из которых имеет размер, равный первому.Парадокс фон Неймана — двумерный аналог.
  • Парадоксальный набор : Набор, который можно разделить на два набора, каждый из которых эквивалентен оригиналу.
• Парадокс береговой линии : периметр суши в целом плохо определен.
• Парадокс вращения монеты : монета, вращающаяся по краю идентичной монеты, сделает полный оборот, пройдя только половину окружности неподвижной монеты.
• Рог Габриэля : или Труба Торричелли : простой объект с конечным объемом, но с бесконечной площадью поверхности. Кроме того, множество Мандельброта и различные другие фракталы покрыты конечной площадью, но имеют бесконечный периметр (фактически, на границе множества Мандельброта нет двух различных точек, до которых можно добраться друг от друга, перемещаясь на конечное расстояние вдоль этой границы, что также подразумевает, что в некотором смысле вы не пойдете дальше, если пройдете «неправильным путем» вокруг набора, чтобы добраться до ближайшей точки).
• Парадокс Хаусдорфа : Существует счетное подмножество C сферы S такое, что S \ C равноразложимо с двумя копиями самого себя.
• Набор Никодима : Набор, содержащийся в и с той же мерой Лебега, что и единичный квадрат, но для каждой его точки существует прямая линия, пересекающая множество Никодима только в этой точке.
• Выворот сферы : Сфера топологически может быть вывернута наизнанку.

Теория принятия решений

• Парадокс Абилина : Люди могут принимать решения, основанные не на том, что они на самом деле хотят делать, а на том, что, по их мнению, хотят делать другие люди, в результате каждый решает сделать то, что на самом деле никто не хочет делать, но только то, что, как они думали, хотели делать все остальные.
• Парадокс распределения : Некоторые системы распределения представления могут давать неинтуитивные результаты из-за округления
• Парадокс Стрелка : При наличии более двух вариантов ни одна система не может обладать всеми атрибутами идеальной системы голосования одновременно.
• Буриданова задница : Как можно сделать рациональный выбор между двумя равноценными результатами?
• Парадокс сетевых магазинов : Даже те, кто лучше знает, играют в так называемую игру сетевых магазинов иррационально.
• Парадокс принятия решений : Выбор наилучшего метода принятия решений сам по себе является проблемой решения.
• Парадокс Эллсберга : Люди проявляют неприятие двусмысленности (в отличие от избегания риска), что противоречит теории ожидаемой полезности.
• Парадокс Фенно : Убеждение, что люди в целом не одобряют Конгресс Соединенных Штатов в целом, но поддерживают Конгрессмена из своего избирательного округа.
• Парадокс Фредкина : Чем больше схожих двух вариантов, тем больше времени агент, принимающий решения, тратит на принятие решения.
• Зеленый парадокс : Политика, направленная на сокращение будущих выбросов CO ₂ , может привести к увеличению выбросов в настоящее время.
• Дилемма ежа : или Парадокс любовника Несмотря на добрую волю, человеческая близость не может произойти без существенного взаимного вреда.
• Парадокс изобретателя : Легче решить более общую проблему, которая охватывает специфику искомого решения.
• Загадка с токсином Кавки : Может ли намереваться выпить несмертельный токсин, если для получения награды нужно только намерение?
• Теория скопления мотивации: Добавление стимулов к определенному поведению может иногда иметь неприятные последствия и фактически приводить к уменьшению такого поведения.
• Вилка Мортона : разновидность ложной дилеммы, в которой противоречивые наблюдения приводят к одному и тому же выводу.
• Парадокс навигации : Повышенная точность навигации может привести к увеличению риска столкновения.
• Парадокс Ньюкома : Как вести игру против всеведущего противника?
• Парадокс толерантности : Следует ли терпеть нетерпимость, если нетерпимость уничтожает возможность толерантности?
• Парадокс голосования : Также известен как парадокс Дауна.Для рационального, корыстного избирателя затраты на голосование обычно превышают ожидаемые выгоды, так почему же люди продолжают голосовать?
• Парадокс Паррондо : Можно сыграть две проигрышные партии поочередно, чтобы в конечном итоге выиграть.
• Профилактический парадокс : Для того, чтобы один человек получил пользу, многим людям необходимо изменить свое поведение, даже если они не получают выгоды или даже страдают от этого изменения.
• Дилемма заключенного : Два человека могут не сотрудничать, даже если это в их интересах.
• Парадокс голосования : Также известен как парадокс Кондорсе и парадокс голосования. Группа отдельно рациональных индивидов может иметь предпочтения, которые в совокупности иррациональны.
• Парадокс силы воли : Те, кто держит свой разум открытым, более целеустремленны и более мотивированы, чем те, кто заявляет о своих целях самим себе.

Физика

• Парадокс холодных тропиков : Противоречие между смоделированными оценками тропических температур в теплые, свободные ото льда периоды мелового периода и эоцена и более низкими температурами, которые предполагают наличие косвенных данных.
• Парадокс непреодолимой силы : Что произойдет, если непреодолимая сила поразит неподвижный объект?
• Парадокс места : Если все, что существует, имеет место, в этом месте должно быть место, и так до бесконечности.
• Парадокс проса : Когда просо падает, оно не издает звука, но когда падает тысяча зерен, они падают, поэтому многие из ничего становятся чем-то.
• Движущиеся строки : предположим, что две строки движутся за неподвижным рядом в противоположных направлениях.Если член движущегося ряда проходит мимо члена стационарного ряда в неделимый момент времени, он проходит мимо двух членов ряда, который движется в другом направлении в этот момент времени.

Астрофизика

Классическая механика

• Ахиллес и черепаха : Если черепаха опережает Ахилла, к тому времени, когда Ахиллес достигнет текущего положения черепахи, черепаха продвинется немного дальше вперед, что будет продолжаться бесконечно.
• Парадокс лучника : Чтобы поразить цель, стрелок должен целиться не прямо в нее, а немного в сторону. Не путать с парадоксом стрелы.
• Arrow paradox Если мы разделим время на дискретные срезы нулевой длительности, в каждом из них не происходит никакого движения, поэтому, взяв их все как единое целое, движение невозможно.
• Гидростатический парадокс : массивный линкор может плавать в нескольких литрах воды.
• Парадокс колеса Аристотеля : Катящиеся соединенные концентрические колеса, кажется, имеют одинаковое расстояние со своими окружностями, хотя окружности разные.
• Парадокс Кэрролла : угловой момент палки должен быть равен нулю, но это не так.
• Парадокс Даламбера : Течение невязкой жидкости не создает результирующей силы на твердое тело.
• Парадокс Кнудсена : Основываясь на уравнениях Навье – Стокса, можно было бы ожидать, что поток массы в канале будет уменьшаться с увеличением числа Кнудсена, но есть отчетливый минимум около числа Кнудсена 0,8.
• Парадокс Денни : Обитающие на поверхности членистоногие (например, водомер) не должны иметь возможности двигаться по горизонтали.
• Парадокс дихотомии : Чтобы достичь своей цели, воздушная стрела должна сначала достичь бесконечного числа средних точек между ее текущим положением и целью.
• Elevator paradox : Даже если ареометры используются для измерения плотности жидкости, ареометр не будет показывать изменения плотности жидкости, вызванные изменением атмосферного давления.
• Спринклер Фейнмана : В каком направлении разбрызгиватель вращается, когда он погружен в резервуар и заставлен всасывать окружающую жидкость?
• Купол Нортона : Существуют ли недетерминированные системы в механике Ньютона?
• Парадокс Пенлеве : Динамика твердого тела с контактом и трением несовместима.
• Парадокс чайных листьев : Когда чашка чая перемешивается, листья собираются в центре, хотя центробежная сила толкает их наружу.
• Загрязнение на верхнем уровне : Когда жидкость переливается из более высокого контейнера в более низкий, частицы могут подниматься вверх по падающей воде.

Космология

• Парадокс Бентли : В ньютоновской вселенной гравитация должна стягивать всю материю в одну точку.
• Мозг Больцмана : Если бы Вселенная, которую мы наблюдаем, возникла в результате случайных термодинамических флуктуаций, она с гораздо большей вероятностью была бы простой, чем наблюдаемая нами сложная.Самый простой случай — это просто мозг, плавающий в вакууме, обладающий вашими мыслями и ощущениями.
• Парадокс Ферми : Если, как предполагают различные аргументы, во Вселенной существует множество других разумных видов, то где они? Разве их присутствие не должно быть очевидным?
• Парадокс тепловой смерти : Если бы Вселенная была бесконечно старой, она была бы в термодинамическом равновесии, что противоречит тому, что мы наблюдаем.
• Парадокс Ольберса : Почему ночное небо темное, если есть бесконечное количество звезд, покрывающих каждую часть небесной сферы?

Электромагнетизм

• Парадокс Фарадея : Очевидное нарушение закона электромагнитной индукции Фарадея.

Квантовая механика

• Эффект Ааронова – Бома : На заряженную частицу действует электромагнитное поле, даже если она не имеет локального контакта с этим полем
• Теорема Белла : Почему измеренные квантовые частицы не удовлетворяют математической теории вероятностей?
• Эксперимент с двумя щелями : Материя и энергия могут действовать как волна или как частица в зависимости от эксперимента.
• Парадокс Эйнштейна – Подольского – Розена : Могут ли отдаленные события влиять друг на друга в квантовой механике?
• Парадокс экстинкции : В пределе малых длин волн полное сечение рассеяния непроницаемой сферы в два раза больше ее геометрической площади поперечного сечения (что является значением, полученным в классической механике). ^[3]
• Парадокс Харди : Как мы можем делать выводы о прошлых событиях, которых мы не наблюдали, и в то же время признавать, что их наблюдение влияет на реальность, о которой мы делаем выводы?
• Парадокс Клейна : Когда потенциал потенциального барьера становится подобным массе падающей частицы, он становится прозрачным.
• Задача Мотта : Сферически-симметричные волновые функции при наблюдении создают линейные треки частиц.
• Парадокс квантовой LC-цепи : Энергия, накопленная на емкости и индуктивности, не равна энергии основного состояния квантового осциллятора. ^{[ требуется ссылка ]}
• Квантовая псевдотелепатия : Два игрока, которые не могут общаться, выполняют задачи, которые, по-видимому, требуют прямого контакта.
• Квантовый эффект Зенона : ( парадокс Тьюринга ) повторяя парадокс Зенона, квантовая частица, которая постоянно наблюдается, не может изменить свое состояние
• Парадокс кота Шредингера : Согласно копенгагенской интерпретации квантовой механики, кошка может быть одновременно живой и мертвой, пока ее не наблюдают.
• Принцип неопределенности : Существует фундаментальный предел точности, с которой могут быть известны определенные пары физических свойств частицы, известные как дополнительные переменные, такие как положение и импульс. Это часто путают с аналогичным эффектом в физике, который называется эффектом наблюдателя

Относительность

Термодинамика

Биология

• Антарктический парадокс : В некоторых районах Мирового океана концентрации фитопланктона низкие, несмотря на то, что там явно достаточно питательных веществ.
• Загадка значения C : Размер генома не коррелирует со сложностью организма. Например, у некоторых одноклеточных организмов геномы намного больше, чем у человека.
• Парадокс Коула : Даже крошечное преимущество в плодовитости одного дополнительного потомства будет способствовать развитию семелпарности.
• Парадокс Грея : Несмотря на свою относительно небольшую мышечную массу, дельфины могут плавать с высокой скоростью и получать большие ускорения.
• Hormesis : Воздействие малых доз токсинов может иметь положительные эффекты.
• Парадокс Лека : Устойчивый выбор самками определенных ценностей мужских черт должен разрушить генетическую вариативность мужских черт и тем самым лишить возможности выбора, но выбор остается.
• Парадокс Ломбарда : При подъеме и вставании из положения сидя или сидя на корточках и подколенные сухожилия, и четырехглавые мышцы сокращаются одновременно, несмотря на то, что они являются антагонистами друг друга.
• Парадокс обогащения : Увеличение количества пищи, доступной для экосистемы, может привести к нестабильности и даже к исчезновению.
• Парадокс пестицидов : Применение пестицида к вредителю может увеличить численность вредителя.
• Парадокс планктона : Почему существует так много различных видов фитопланктона, хотя конкуренция за одни и те же ресурсы имеет тенденцию сокращать количество видов?
• Парадокс Шермана : Аномальный образец наследования при синдроме ломкой Х-хромосомы.
• Парадокс таксономических границ : В прошлом концепция таксона могла частично совпадать.
• Временной парадокс (палеонтология) : Когда жили предки птиц?

Здоровье и питание

• Французский парадокс : Наблюдение за тем, что французы страдают относительно низкой заболеваемостью ишемической болезнью сердца, несмотря на то, что их диета относительно богата насыщенными жирами, которые считаются основной причиной такого заболевания.
• Глюкозный парадокс : Большое количество гликогена в печени не может быть объяснено его малым поглощением глюкозы.
• Парадокс испаноязычных : Вывод о том, что латиноамериканцы в Соединенных Штатах, как правило, имеют значительно лучшее здоровье, чем среднее население, несмотря на то, что предсказывают их совокупные социально-экономические показатели.
• Израильский парадокс : Наблюдение за тем, что израильтяне страдают относительно высокой заболеваемостью ишемической болезнью сердца, несмотря на то, что в их рационе очень мало насыщенных жиров, которые считаются основной причиной такого заболевания в питании.
• Мексиканский парадокс : мексиканские дети обычно имеют более высокий вес при рождении

.

Список парадоксов

Это список парадоксов , сгруппированных по тематике. Обратите внимание на то, что многие из перечисленных парадоксов имеют четкое разрешение — см. Классификацию парадоксов Куайна.

Логический, нематематический

* Парадокс следствия: несовместимые посылки всегда делают аргумент действительным.
* Парадокс ворона (или вороны Хемпеля): наблюдение за зеленым яблоком увеличивает вероятность того, что все вороны будут черными.
* Парадокс лошади: все лошади одного цвета.
* Неожиданный парадокс повешения: день повешения будет сюрпризом, так что этого не может быть вообще, так что это будет сюрприз. Парадокс «Бутылочного беса» использует аналогичную логику.
* Парадокс пьющего: в любом пабе есть такой посетитель, что, если он или она пьет, то пьют все в пабе.
* Парадокс Кэрролла: «Все, что логика достаточно хороша, чтобы сказать мне, стоит« записать »…»
* Парадокс лотереи: философски оправдано верить, что каждый отдельный лотерейный билет не выиграет, но это не оправдано верить что ни один лотерейный билет не выиграет.

elf-referential

Эти парадоксы имеют общее противоречие, возникающее из-за самоотнесения.
* Парадокс Берри: фраза «первое число, которое нельзя назвать менее чем десятью словами», кажется, называет его девятью словами.
* Парадокс Карри: «Если это предложение верно, конец света наступит через неделю».
* Парадокс Эпименида: критянин говорит: «Все критяне лжецы».
* Парадокс исключений: «Если есть исключение для каждого правила, то каждое правило должно иметь по крайней мере одно исключение, исключение из этого состоит в том, что оно не имеет исключения.
* Парадокс Греллинга-Нельсона: является ли слово «гетерологический», означающее «неприменимый к самому себе», гетерологическим словом? (Другой близкий родственник парадокса Рассела.)
* Намеренно пустая страница: многие документы содержат страницы, на которых находится текст «Эта страница намеренно оставлена ​​пустой» печатается, что делает страницу не пустой.
* Парадокс лжеца: «Это предложение неверно». Это канонический парадокс самореференции. Также «Ответ на этот вопрос нет?»
* Комбинатор Y в лямбда-исчислении и комбинаторной логике был назван парадоксальным комбинатором, поскольку он связан с антиномиями самореференции.
* Парадокс Петрония: «Умеренность во всем, включая умеренность».
* Парадокс Куайна: «дает ложь, когда добавляется к его собственной цитате» дает ложь, когда добавляется к своей собственной цитате.
* Парадокс суда: студент юридического факультета соглашается заплатить своему учителю после победы в его первом деле. Затем учитель предъявляет иск ученику (который еще не выиграл дело) о выплате.
* Парадокс Рассела: содержит ли набор всех тех множеств, которые не содержат самих себя? Рассел популяризировал это парадоксом парикмахера: взрослый парикмахер-мужчина, который бреет всех мужчин, которые не бреются, и никого другого.
* Парадокс Ричарда: кажется, мы можем использовать простой английский язык для определения десятичного разложения таким образом, который противоречит сам себе.
* Статусный парадокс: Существование одновременно в двух противоположных состояниях бытия ex. «Курильщики бросают курить», что означает, что тот, кто курит, бросает курить, но если он бросает курить, это означает, что либо курение никогда не произойдет, либо курение прекратится. но после того, как «бросят» курить, они бросят курить. Это будет означать, что бросивший курить перейдет к курению, что сделает его курильщиком.

Неопределенность

* Корабль Тесея (он же старый топор Джорджа Вашингтона или Деда): похоже, что вы можете заменить любой компонент корабля, и это будет тот же корабль. Таким образом, вы можете заменить их все или по одному, и это будет тот же корабль. Но тогда вы можете взять все оригинальные части и собрать из них корабль. Это тоже тот же корабль, с которого вы начали.
* Парадокс Сорита: Одна песчинка — это не куча. Если у вас нет кучи, то добавление только одной песчинки не даст вам кучи.Тогда никакое количество песчинок не превратится в кучу. Точно так же один волос не может сделать разницу между тем, чтобы быть лысым или не быть лысым. Но тогда, если вы будете удалять по одному волосу за раз, вы никогда не станете лысым. Точно так же один доллар не сделает вас богатым, поэтому, если вы будете продолжать в том же духе, по доллару за раз, вы никогда не станете богатым, сколько бы вы ни заработали.

Математический

: «См. Также:»
* Парадокс распределения: некоторые системы распределения представления могут давать неинтуитивные результаты из-за округления
** Парадокс Алабамы: увеличение общего количества мест может привести к сокращению мест на один блок.
** Парадокс новых состояний: добавление нового состояния или блока голосования может увеличить количество голосов другого.
** Парадокс населения: быстрорастущий штат может потерять голоса в пользу медленно растущего штата.
* Арифметические парадоксы: доказательства очевидных противоречий; например, «доказательство» того, что 2 = 1, путем написания огромного выражения и деления на другое выражение, значение которого равно нулю.
* Парадокс Стрелка / Парадокс голосования: при наличии более двух вариантов ни одна система не может иметь все атрибуты идеальной системы голосования одновременно.
* Парадокс Кондорсе: группа отдельно рациональных индивидов может иметь предпочтения, которые в совокупности иррациональны.
* Парадокс лифта: может показаться, что лифты в основном движутся в одном направлении, как если бы они производились в центре здания и разбирались на крыше и в подвале.
* Парадокс интересного числа: первое число, которое можно считать «скучным», а не «интересным», становится интересным именно из-за этого.
* Непереходный кубик: у вас может быть три кубика, называемые A, B и C, так что A, скорее всего, выиграет в броске против B, B, скорее всего, выиграет в броске у C, а C, вероятно, выиграет в бросок против А.
* Парадокс низкой массы тела при рождении: Низкая масса тела при рождении и курящие матери способствуют более высокому уровню смертности. Младенцы курильщиков имеют более низкий средний вес при рождении, но дети с низким весом при рождении, рожденные от курильщиков, имеют более низкий уровень смертности, чем другие дети с низким весом при рождении. (Частный случай парадокса Симпсона.)
* Парадокс пропущенного доллара: неверная логика создает впечатление, будто пропал доллар из ресторанного счета. Не в том же классе, что и другие.
* Парадокс наименьшего числа описывает, как катящийся объект должен быть в состоянии достичь скорости наименьшего положительного числа.

tatistics

* Закон Бенфорда: в списках чисел из многих реальных источников данных первая цифра 1 встречается гораздо чаще, чем другие.
* Парадокс Берксона: усложняющий фактор, возникающий при статистических тестах пропорций
* Из корреляции вполне можно сделать неправильные выводы. Например, в городах с большим количеством церквей, как правило, выше уровень преступности, потому что оба они являются результатом более высокой численности населения. Однажды профессиональная организация обнаружила, что экономисты со степенью доктора философии.На самом деле у Д. была более низкая средняя зарплата, чем у людей со степенью бакалавра наук, но выяснилось, что это потому, что те, у кого есть докторская степень. работал в академических кругах, где зарплаты, как правило, ниже. Это также называется ложными отношениями.
* Парадокс осмотра: почему вы будете ждать этот автобус дольше, чем следовало бы.
* Парадокс Линдли: крошечные ошибки в нулевой гипотезе увеличиваются при анализе больших наборов данных, что приводит к ложным, но очень статистически значимым результатам
* Феномен Уилла Роджерса: математическая концепция среднего, определяемого как среднее или медианное, приводит к явно парадоксальным результатам — например, возможно, что перемещение статьи из энциклопедии в словарь увеличит среднюю длину статьи в «обеих» книгах.

Вероятность

: «См. Также:»
* Парадокс Бертрана (вероятность): Различные определения случайности, основанные на здравом смысле, дают совершенно разные результаты.
* Парадокс дня рождения: какова вероятность того, что у двух человек в комнате день рождения одинаковый?
* Парадокс Бореля: условные функции плотности вероятности не инвариантны относительно преобразований координат.
* Мальчик или девочка: В семье с двумя детьми есть как минимум один мальчик. Какова вероятность, что у него есть девушка?
* Проблема Монти Холла: неинтуитивное следствие условной вероятности.
* Парадокс галстука: Ставка между двумя людьми, кажется, выгодна им обоим. По сути, очень похоже на парадокс двух конвертов.
* Парадокс Симпсона: ассоциация субпопуляций в популяции может быть обратной. Похоже, что два набора данных по отдельности подтверждают определенную гипотезу, но при совместном рассмотрении они подтверждают противоположную гипотезу.
* Проблема «Спящей красавицы»: проблема вероятности, на которую можно правильно ответить как половину или одну треть, в зависимости от того, как подойти к вопросу.
* Проблема с тремя картами: Как определить цвет нижней стороны карты при вытягивании случайной карты?
* Парадокс двух конвертов: вам дают два неотличимых конверта и говорят, что в одном содержится вдвое больше денег, чем в другом. Вы можете открыть один конверт, изучить его содержимое, а затем, не открывая другой, выбрать, какой конверт взять.

Infinity и infinitestimals

* 0,999 … точно равно единице; многим людям трудно поверить в это.
* Парадокс Бурали-Форти: если бы порядковые числа образовали набор, это был бы порядковый номер, который меньше его самого.
* Парадокс Галилея: хотя большинство чисел не квадраты, чисел не больше, чем квадратов. (См. Также диагональный аргумент Кантора)
* Парадокс Гильберта о Гранд Отеле: если отель с бесконечно большим количеством номеров заполнен, он все равно может принять больше гостей.
* Парадокс Сколема: Счетно бесконечные модели теории множеств содержат несчетное бесконечное множество.
* Сверхзадачи могут приводить к парадоксам, таким как парадокс Росса-Литтлвуда и парадокс Бенардете.
* Парадоксы Зенона: «Вы никогда не достигнете точки B из точки A, так как вы всегда должны пройти туда половину пути, и половину половины, половину этой половины и так далее….»(Это тоже физический парадокс.)

Геометрия и топология

* Парадокс Банаха – Тарского: Разрежьте шар на 5 частей, соберите части заново, чтобы получить два шара, оба равных по размеру первому.
* Ден: Невозможно превратить правильный тетраэдр в параллелепипед, разрезав его на многогранные части.
* Рог Габриэля или труба Торричелли: простой объект с конечным объемом, но бесконечной площадью поверхности. Кроме того, множество Мандельброта и другие фракталы имеют конечную форму, но имеют бесконечный периметр (на самом деле нет двух различных точек на границе множества Мандельброта, в которые можно попасть друг от друга, перемещаясь на конечное расстояние вдоль этой границы, что также означает, что в некотором смысле, вы не пойдете дальше, если пройдете «не туда» по съемочной площадке, чтобы добраться до ближайшей точки).
* Парадокс Хаусдорфа: существует счетное подмножество C сферы S такое, что SC равноразложимо с двумя копиями самого себя.
* Парадокс береговой линии: периметр суши в целом нечеткий.

* Парадокс Смейла: сферу топологически можно вывернуть наизнанку.
* Пазл с отсутствующим квадратом: Две похожие фигуры, построенные из одних и тех же частей, имеют разные области.

Теория принятия решений

* Парадокс Абилина: люди могут принимать решения, основываясь не на том, что они на самом деле хотят делать, а на том, что, по их мнению, хотят делать другие люди, в результате каждый решает сделать то, что на самом деле никто хочет делать, но только то, что они думали, что все остальные хотят делать.
* Буриданова задница: Как сделать рациональный выбор между двумя равноценными результатами?
* Форк Мортона: выбор между неприятными альтернативами.
* Парадокс гедонизма: когда кто-то стремится к самому счастью, он несчастен; но когда человек преследует что-то еще, он достигает счастья.
* Парадокс Ньюкомба: как вести игру против всеведущего противника?
* Токсиновая загадка Кавки: Можно ли «намереваться» выпить несмертельный токсин, если намерение — единственное, что нужно для получения награды?

Химическая промышленность

* Парадокс SAR: исключения из принципа, согласно которому небольшое изменение в молекуле вызывает небольшое изменение ее химического поведения, часто бывают серьезными.
* Парадокс Левинталя: промежуток времени, в течение которого белковая цепь находит свое свернутое состояние, на много порядков меньше, чем было бы, если бы она свободно перебирала все возможные конфигурации.

Физический

* Парадокс Архимеда: массивный линкор может плавать в нескольких литрах воды.
* Парадокс космического корабля Белла: относительно теории относительности.
* Теорема Белла: Измеренные квантовые частицы не удовлетворяют математической теории вероятностей.
* Информационный парадокс черной дыры: Черные дыры нарушают общепринятый научный принцип — информацию нельзя уничтожить.
* Парадокс Браесса: иногда добавление дополнительной емкости в сеть может снизить общую производительность.
* Парадокс Кэрролла: угловой момент палки должен быть равен нулю, но это не так.
* Парадокс Даламбера: невязкая жидкость не вызывает сопротивления.
* Парадокс Денни: живущие на поверхности членистоногие (такие как водомер) не должны иметь возможности двигаться по горизонтали.
* Парадокс Эренфеста: Кинематика жесткого вращающегося диска.
* Парадокс Эйнштейна-Подольского-Розена: могут ли отдаленные события влиять друг на друга в квантовой механике?
* Парадокс Ферми: Если во Вселенной существует, как можно предположить, множество других разумных видов, то где они? Разве их присутствие не должно быть очевидным?
* Парадокс Гиббса: является ли энтропия экстенсивной переменной в идеальном газе?
* Парадокс ГЗК: наблюдались космические лучи высоких энергий, которые, кажется, нарушают предел Грейзена-Зацепина-Кузьмина, который является следствием специальной теории относительности.
* Парадокс непреодолимой силы: что случится, если непреодолимая сила ударит по неподвижному объекту?
* Лестничный парадокс: классическая проблема относительности.
* Парадокс Лошмидта: почему происходит неизбежное увеличение энтропии, если законы физики инвариантны относительно обращения времени? Симметрия физических законов относительно обращения времени, по-видимому, позволяет нарушить второй закон термодинамики.
* Парадокс Мпембы: Горячая вода может при определенных условиях замерзать быстрее, чем холодная, даже если она должна пройти более низкую температуру на пути к замерзанию.
* Парадокс Ольберса: почему ночное небо черное, если звезд бесконечное множество?
* Онтологический парадокс: может ли путешественник во времени посылать себе информацию без внешнего источника?
* Парадокс кошки Шредингера: квантовый парадокс. Кошка жива или мертва до того, как мы посмотрим?
* Парадокс Суппли: плавучесть релятивистского объекта (такого как пуля), по-видимому, изменяется, когда система отсчета изменяется с той, в которой пуля находится в состоянии покоя, на систему, в которой жидкость покоится.
* Временной парадокс (палеонтология): Когда жили предки птиц?
* Парадокс близнецов: загадочное следствие специальной теории относительности: путешествующий человек возвращается моложе своего однояйцевого близнеца, который остался на месте.

Философский

* Эпикурейский парадокс: существование зла кажется несовместимым с существованием всемогущего и заботливого Бога.
* Парадокс Фитча: если все истины познаваемы, то фактически должны быть известны все истины.
* Дедушка парадокс: вы путешествуете во времени и убиваете своего дедушку до того, как он встречает вашу бабушку, что исключает ваше собственное зачатие и, следовательно, вы не можете вернуться в прошлое и убить своего деда.
* Парадокс Хаттона: Если спросить себя: «Я сплю?» во сне доказывает, что есть, что доказывает в бодрствующей жизни?
* Либеральный парадокс: «Минимальная свобода» несовместима с оптимальностью Парето.
* Парадокс простого дополнения: неужели большая часть населения с трудом переносит жизнь лучше, чем маленькое счастливое население?
* Парадокс Мура: «Дождь идет, но я не верю, что он есть».
* Парадокс Ньюкома: Парадоксальная игра между двумя игроками, один из которых может предсказать действия другого.
* Нигилистический парадокс: если истины не существует, утверждение «истины не существует» является истиной, тем самым оказываясь неверным.
* Парадокс всемогущества: Может ли всемогущее существо создать камень, слишком тяжелый для поднятия?
* Парадокс гедонизма: в поисках счастья не найти счастья.
* Парадокс предопределения: человек путешествует во времени, чтобы выяснить причину знаменитого пожара. Находясь в здании, где начался пожар, он случайно опрокидывает керосиновый фонарь и вызывает пожар — тот самый огонь, который вдохновил его много лет спустя на путешествие во времени. С этим тесно связан онтологический парадокс, в котором в результате путешествия во времени информация или объекты, кажется, не имеют начала.
* Парадоксы Зенона: «Вы никогда не достигнете точки B из точки A, так как вы всегда должны пройти туда половину пути, половину половины, половину этой половины и так далее… «(Это тоже парадокс бесконечности)

Экономический

:» См. Также: «

* Парадокс Абилина: группе людей часто приходится принимать решения вопреки личным интересам или взглядам каждого члена группы.
* Парадокс Алле: изменение возможного исхода, которое разделяется различными альтернативами, влияет на выбор людей среди этих альтернатив, что противоречит теории ожидаемой полезности.
* Парадокс Бертрана: два игрока, достигнув состояния равновесия по Нэшу, оба оказываются без прибыли.
* Парадокс алмаз-вода (или парадокс ценности) Вода более полезна, чем алмазы, но при этом намного дешевле.
* Парадокс Эджворта: при ограниченных производственных мощностях равновесия может не быть.
* Парадокс Эллсберга: люди проявляют неприятие двусмысленности (в отличие от неприятия риска), что противоречит теории ожидаемой полезности.
* Парадокс Гибсона: почему процентные ставки и цены коррелировали?
* Парадокс Гиффена: повышение цен на хлеб заставляет бедняков есть его больше.
* Парадокс Джевонса: повышение эффективности ведет к еще большему увеличению спроса.
* Парадокс Леонтьева: некоторые страны экспортируют трудоемкие товары и импортируют капиталоемкие товары, что противоречит теории Хекшера-Олина.
* Парадокс бережливости: если каждый будет экономить больше денег во время рецессии, то совокупный спрос упадет и, в свою очередь, снизит общие сбережения населения.
* Парадокс Паррондо: можно поочередно сыграть две проигрышные партии, чтобы в конечном итоге выиграть.
* Парадокс производительности (также известный как компьютерный парадокс Солоу): производительность труда может снизиться, несмотря на технологические усовершенствования.
* Санкт-Петербург: парадокс: люди предлагают скромную плату за вознаграждение бесконечной ожидаемой ценности.

ee также

* Парадокс брекетинга
* Парадокс масляной кошки, юмористический пример парадокса из противоречащих народным сказкам
* Этика
* Невозможный объект
* Доказательство того, что 0,999 … равно 1
* Логическая ошибка
* Головоломка

Фонд Викимедиа.
2010.

.

10 поразительных парадоксов

Парадокс — это утверждение или проблема, которые либо приводят к двум совершенно противоположным (но возможным) результатам, либо предоставляют доказательство того, что идет вразрез с тем, что мы интуитивно ожидаем. Парадоксы были центральной частью философского мышления на протяжении веков и всегда готовы бросить вызов нашей интерпретации в остальном простых ситуаций, перевернув с ног на голову то, что мы могли бы считать истиной, и представить нам доказуемо правдоподобные ситуации, которые на самом деле столь же доказуемы. невозможно.Смущенный? Вы должны быть.

1. АХИЛЛ И ЧЕРЕПАХА

Парадокс Ахилла и черепахи — одно из ряда теоретических рассуждений о движении, выдвинутых греческим философом Зеноном Элейским в 5 веке до нашей эры. Он начинается с того, что великий герой Ахиллес бросает вызов черепахе на беговую дорожку. Для справедливости он соглашается дать черепахе фору, скажем, на 500 метров. Когда начинается гонка, Ахилл, что неудивительно, начинает бежать со скоростью, намного превышающей скорость черепахи, так что к тому времени, когда он достиг отметки 500 метров, черепаха прошла всего на 50 метров дальше его.Но к тому времени, когда Ахилл достиг отметки 550 метров, черепаха прошла еще 5 метров. И к тому времени, когда черепаха достигла отметки 555 м, она прошла еще 0,5 м, затем 0,25 м, затем 0,125 м и так далее. Этот процесс продолжается снова и снова на бесконечной серии все меньших и меньших расстояний, при этом черепаха всегда движется вперед на , а Ахиллес всегда догоняет.

Логически это, кажется, доказывает, что Ахиллес никогда не сможет догнать черепаху — когда бы он ни достиг того места, где была черепаха, у него всегда будет оставшееся расстояние, каким бы маленьким оно ни было.За исключением, конечно, интуитивного знания, что он может обогнать черепаху. Уловка здесь заключается не в том, чтобы думать о парадоксе Ахилла Зенона в терминах расстояний и рас, а скорее как в качестве примера того, как любое конечное значение всегда можно разделить бесконечное количество раз, независимо от того, насколько маленькими могут стать его деления.

2. ПАРАДОКС BOOTSTRAP

The Bootstrap Paradox — это парадокс путешествия во времени, который ставит под сомнение то, как то, что взято из будущего и помещено в прошлое, могло вообще когда-либо возникнуть.Это обычный образ, используемый писателями-фантастами и вдохновляющий сюжеты во всем, от Доктора Кто до Билла и Теда фильмов, но один из самых запоминающихся и простых примеров — профессор Дэвид Туми из Массачусетского университета и использовал в своей книге Новые путешественники во времени — включает автора и его рукопись.

Представьте, что путешественник во времени покупает копию Гамлета в книжном магазине, путешествует во времени в елизаветинский Лондон и передает книгу Шекспиру, который затем копирует ее и заявляет, что это его собственная работа.В течение последующих столетий книга Гамлет переиздавалась и воспроизводилась бесчисленное количество раз, пока, наконец, ее копия не оказалась в том же книжном магазине, где путешественник во времени находит ее, покупает и отнесет Шекспиру. Кто же тогда написал Гамлет ?

3. ПАРАДОКС МАЛЬЧИКА ИЛИ ДЕВОЧКИ

Представьте себе, что в семье двое детей, один из которых, как мы знаем, мальчик. Какова же тогда вероятность того, что второй ребенок — мальчик? Очевидный ответ — сказать, что вероятность составляет 1/2 — в конце концов, другой ребенок может быть только или мальчик или девочка, и шансы, что ребенок родится мальчиком или девочкой, равны (по сути ) равный.Однако в семье с двумя детьми существует четыре возможных комбинации детей: два мальчика (MM), две девочки (FF), старший мальчик и младшая девочка (MF), а также старшая девочка и младший мальчик ( FM). Мы уже знаем, что один из детей — мальчик, то есть мы можем исключить комбинацию FF, но это оставляет нам три равновозможных комбинации детей, в которых по крайней мере один — мальчик, а именно MM, MF и FM. Это означает, что вероятность того, что другой ребенок будет мальчиком — ММ — должна быть 1/3, а не 1/2.

4. КАРТОЧНЫЙ ПАРАДОКС

Представьте, что вы держите в руке открытку, на одной стороне которой написано: «Утверждение на другой стороне этой открытки верно». Мы назовем это Утверждение А. Переверните карточку, и на противоположной стороне будет написано: «Утверждение на другой стороне этой карточки ложно» (Утверждение Б). Однако попытка приписать какую-либо истину утверждению A или B приводит к парадоксу: если A истинно, то B также должно быть истинным, но для того, чтобы B было истинным, A должно быть ложным.Напротив, если A ложно, то B тоже должно быть ложным, что в конечном итоге должно сделать A истинным.

Карточный парадокс, изобретенный британским логиком Филипом Журденом в начале 1900-х годов, представляет собой простую вариацию так называемого «парадокса лжеца», в котором присвоение значений истинности утверждениям, которые претендуют на то, чтобы быть истинными или ложными, приводит к противоречию. Следующая запись в нашем списке — , еще более сложная вариация парадокса лжеца.

5. ПАРАДОКС КРОКОДИЛОВ

Крокодил хватает мальчика с берега реки.Его мать умоляет крокодила вернуть его, на что крокодил отвечает, что он вернет мальчика благополучно, только если мать сможет правильно угадать, действительно ли он вернет мальчика. Нет проблем, если мать угадает, что крокодил вернет его — если она права, он возвращается; если она ошибается, крокодил удерживает его. Если она ответит, что крокодил , а не вернет его, однако, мы приходим к парадоксу: если она права и крокодил никогда не собирался возвращать ее ребенка, то крокодил должен вернуть его, но при этом ломает его слово и противоречит ответу матери.С другой стороны, если она ошибается и крокодил действительно намеревался вернуть мальчика, крокодил должен затем удержать его, даже если он намеревался этого не делать, тем самым также нарушив свое слово.

Парадокс крокодила — это такая древняя и устойчивая логическая проблема, что в средние века слово «крокодил» стало использоваться для обозначения любой аналогичной сложной дилеммы, когда вы допускаете то, что позже используется против вас, в то время как «крокодил» столь же древнее слово для придирчивого или ошибочного рассуждения.

6.ПАРАДОКС ДИХОТОМИИ

Представьте, что вы собираетесь идти по улице. Чтобы добраться до другого конца, вам сначала нужно пройти половину пути. И чтобы пройти половину пути, вам придется сначала пройти четверть пути. И чтобы пройти там четверть пути, вам придется сначала пройти восьмую часть пути. А перед этим шестнадцатая часть пути туда, затем тридцать вторая пути туда, шестьдесят четвертая часть пути туда и так далее.

В конечном итоге, чтобы выполнить даже простейшую задачу, например, пройтись по улице, вам придется выполнять бесконечное количество более мелких задач — что по определению совершенно невозможно.Не только это, но независимо от того, насколько малой будет первая часть пути, ее всегда можно сократить вдвое, чтобы создать новую задачу; Единственный способ, которым не может быть уменьшено вдвое, — это считать, что первая часть путешествия проходит абсолютно без какого-либо расстояния, и для выполнения задачи по отсутствию какого-либо расстояния вы не можете даже начать свое путешествие в первую очередь.

7. ПАРАДОКС ФЛЕТЧЕРА

Представьте, что флетчер (то есть стрелочник) выпустил одну из своих стрел в воздух.Чтобы стрелка считалась движущейся, она должна постоянно перемещаться с того места, где она сейчас находится, в любое место, где в настоящее время ее нет. Однако парадокс Флетчера гласит, что на протяжении всей своей траектории стрела на самом деле вообще не движется. В любой момент, не имеющий реальной продолжительности (другими словами, моментальный снимок во времени) во время полета, стрелка не может переместиться туда, где она не находится, потому что у нее нет времени для этого. И он не может переместиться туда, где находится сейчас, потому что он уже там.Итак, в данный момент стрелка должна быть неподвижной. Но поскольку все время целиком состоит из мгновений — в каждом из которых стрелка также должна быть неподвижной, — то стрелка фактически должна быть неподвижной все время. За исключением, конечно, нет.

8. ПАРАДОКС БЕСКОНЕЧНОСТИ ГАЛИЛЕЯ

В своей последней письменной работе « Рассуждения и математические демонстрации, относящиеся к двум новым наукам (1638)» легендарный итальянский эрудит Галилео Галилей предложил математический парадокс, основанный на отношениях между различными наборами чисел.С одной стороны, предположил он, есть квадратные числа, такие как 1, 4, 9, 16, 25, 36 и так далее. С другой стороны, есть числа, которые представляют собой , а не квадратов, например 2, 3, 5, 6, 7, 8, 10 и так далее. Сложите эти две группы вместе, и, конечно же, чисел в целом должно быть больше, чем , всего лишь квадратных чисел — или, говоря другими словами, общее количество квадратных чисел должно быть меньше, чем общее количество квадратов и неквадратных чисел вместе. Однако, поскольку каждое положительное число должно иметь соответствующий квадрат, а каждое квадратное число должно иметь положительное число в качестве квадратного корня, не может быть больше одного, чем другого.

Запутались? Ты не единственный. При обсуждении своего парадокса Галилею не оставалось ничего другого, как сделать вывод, что числовые концепции, такие как больше , меньше или меньше , могут применяться только к конечным наборам чисел, а поскольку существует бесконечное количество чисел квадратные и неквадратные числа, эти понятия просто не могут использоваться в этом контексте.

9. КАРТОФЕЛЬНЫЙ ПАРАДОКС

Представьте, что у фермера есть мешок, в котором лежит 100 фунтов картофеля.Он обнаруживает, что картофель на 99% состоит из воды и на 1% твердых веществ, поэтому он оставляет его на солнце на день, чтобы количество воды в нем уменьшилось до 98%. Но когда он возвращается к ним на следующий день, он обнаруживает, что его 100-фунтовый мешок теперь весит всего 50 фунтов. Как это может быть правдой? Что ж, если 99% 100 фунтов картофеля — это вода, то вода должна весить 99 фунтов. 1% твердых веществ должен в конечном итоге весить всего 1 фунт, что дает соотношение твердых веществ и жидкостей 1:99. Но если картофелю дать возможность обезвожиться до 98% воды, твердые вещества теперь должны составлять 2% от веса — соотношение 2:98 или 1:49 — хотя твердые вещества все еще должны весить всего 1 фунт.Вода, в конечном счете, теперь должна весить 49 фунтов, что дает общий вес 50 фунтов, несмотря на снижение содержания воды всего на 1%. Или надо?

Хотя парадоксальный картофельный парадокс и не является истинным парадоксом в строгом смысле слова, он является известным примером того, что известно как достоверный парадокс, в котором основная теория доводится до логического, но очевидно абсурдного заключения.

10. ПАРАДОКС ВОРОНА

Парадокс Ворона, также известный как парадокс Гемпеля, по мнению немецкого логика, предложившего его в середине 1940-х годов, начинается с явно прямого и полностью верного утверждения, что «все вороны черные.Этому соответствует «логически противоположное» (т. Е. Отрицательное и противоречивое) утверждение о том, что «все, что является , а не черным, является , а не вороном» — что, несмотря на то, что кажется совершенно ненужным замечанием, также верно, учитывая что мы знаем, что «все вороны черные». Хемпель утверждает, что всякий раз, когда мы видим черного ворона, это служит подтверждением первого утверждения. Но, в более широком смысле, всякий раз, когда мы видим что-то, что является , а не черным, например яблоко, это тоже следует рассматривать как доказательство, подтверждающее второе утверждение — в конце концов, яблоко не черное и не ворон.

Парадокс здесь в том, что Хемпель очевидно доказал, что вид яблока дает нам свидетельство, каким бы несвязанным оно ни казалось, что вороны черные. Это то же самое, что сказать, что вы живете в Нью-Йорке, — это свидетельство того, что вы не живете в Лос-Анджелесе, или то, что вам 30 лет, — это свидетельство того, что вам не 29. В любом случае, сколько информации может означать одно утверждение?

,

определение парадоксов от The Free Dictionary

Правда, не обойтись без некоторых пропагандистов парадоксов, которые утверждают, что нет необходимой связи между геометрической и моральной неправильностью. Их моральные эксцентричности, такие как их странности в одежде, их дикие теории и парадоксы, были развлечением, которое ее позабавило. но не оказал ни малейшего влияния на ее убеждения. Это универсальный язык Марса, с помощью которого высшие и низшие животные этого мира парадоксов могут общаться в большей или меньшей степени, в зависимости от интеллектуальной сферы их жизни. вид и развитие человека.Хотя не они виноваты, но простаки превозносят их, и глупцы в них верят; и если бы я был верной дуэной, которой должен был быть, его несвежие тщеславия никогда бы не тронули меня, и я бы не поддался таким фразам, как «в смерти я живу», «во льду я горю», «в огне я дрожь »,« безнадежно, надеюсь »,« Я ухожу и остаюсь »и парадоксы того рода, которыми полны их сочинения. Платон наиболее верен характеру своего хозяина, когда он описывает его как« не из этого мира.«И с этим представлением о нем идеальное государство и другие парадоксы республики вполне соответствуют, хотя нельзя показать, что они были спекуляциями Сократа. Я допускаю, что рефлексивное свойство бесконечности иногда подрывает определенные парадоксы лжеца. из конечного списка с n истинами и n-1 ложью. Они подразумевали, что если бы мы действительно могли взяться за вопросы, а не просто говорить о них, мы бы обнаружили «скрытые переменные». Мы бы обнаружили вещи, которые разрешили парадоксы, которые вдохновило датское видение небытия, и реальность снова станет твердой и надежной.Чанг, вице-президент по биометрии в AMAG Pharmaceuticals, предлагает исчерпывающий учебник, который может также служить справочником парадоксов, встречающихся в научных и математических рассуждениях. В каждой главе исследуются парадоксы, присущие определенному аспекту или аспектам самонадеянности текстового потомства. Глобальный маркетинг и реклама: понимание культурных парадоксов, 5-е издание Анекдоты, рассказанные Бергером в тридцатиминутном монологе, являются адаптацией хорошо известных парадоксов: парадоксов движения Зенона и парадокса теории множеств Бертрана Рассела, который касается невозможности существования множества, содержащего самого себя. — Отсюда название выставки: «Не принадлежать себе.Монолог Бергера, написанный Гарсией Торресом совместно с комиком и продюсером Эдуардо Донжуаном, переносит эти интеллектуальные игры в повседневную жизнь, где они порождают абсурдные ситуации. Конечным результатом этих парадоксов в жизни миллениалов стало изменение их счастья как такового. по сравнению с бэби-бумерами.
,