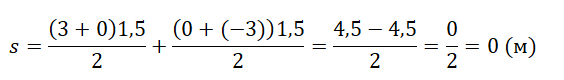Примеры перемещения: Перемещение. Видеоурок. Физика 9 Класс

Перемещение и путь

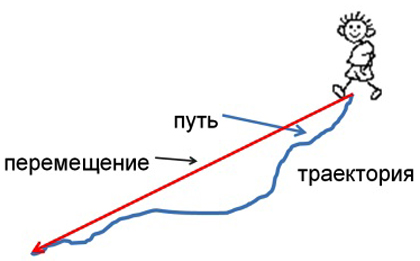
В этой статье я хочу четко разграничить два понятия: путь и перемещение. Тело может переместиться из пункта в пункт по-разному. Путь – это длина траектории, то есть линии, по которой тело двигалось. А перемещение – это результат проделанного пути, то есть кратчайшее расстояние между начальной и конечной точками. Пример: вам надо оказаться на другой стороне реки шириной 100 метров, но мост находится в 10 км. Тогда, чтобы оказаться в нужной точке, придется пилить до моста, через мост и снова 10 километров в обратном направлении. Путь – более 20 км, а перемещение – 100 м! Подумайте, за что мы платим, когда покупаем билет на самолет? Правильно, за перемещение. А ведь самолет может лететь и не по прямой линии, а, например, по кривой, в обход грозовых фронтов. А вот в такси мы платим именно за путь: за конкретную длину дороги, по которой нам пришлось ехать.

Задача 1. В момент времени с тело находилось в точке пространства с координатами  м; м. К моменту времени с тело переместилось в точку с координатами  м; м. Найти время движения тела. Чему равна проекция перемещения на ось ? На ось ? Чему равен модуль перемещения тела?

Первый вопрос задачи, наверное, для первоклассников: очевидно, что тело двигалось 2 с.

Проекция перемещения на ось – это расстояние, которое тело прошло именно по этой оси. Если оно сначала находилось в точке с координатой (-2), а потом достигло точки с координатой (3), то понятно, что искомая проекция равна 5:

Точно так же найдем проекцию перемещения на ось :

Модуль перемещения можно найти, зная проекции:

Заметим, что путь из данных задачи определить нельзя: ведь неизвестно, каким путем тело пришло из первой точки во вторую, можно ведь и в Москву летать через Камчатку…

Задача 2. На рисунке показана траектория движения материальной точки. Ее начальное положение – А, конечное – С. Найти проекции перемещения точки на оси и , модуль перемещения и путь, пройденный точкой.

Задача 2

Тело начало движение из точки , координата которой по оси – 2. А координата точки по той же оси – 8. Поскольку тело после этого не перемещалось по оси , то проекция перемещения на ось равна:

Затем тело двигалось только по оси . Координата точки по оси – 2. Координата точки по оси – 10. Тогда перемещение тела по оси равно:

Путь, пройденный точкой, равен (показан синим цветом):

А модуль перемещения (показан красным):

Механическое движение — материалы для подготовки к ЕГЭ по Физике

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.

Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.

Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.

Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.

Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат . Начало координат является телом отсчёта.

Рисунок 1.

Вектор называется радиус-вектором точки . Координаты точки являются в то же время координатами её радиус-вектора .
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени: .
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.

К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.

Траектория, путь, перемещение.

В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.

Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора .
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке (рис. 2). Тогда путь, пройденный телом, это длина траектории . Перемещение тела — это вектор .

Рисунок 2.

Скорость и ускорение.

Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).

Рисунок 3.

Пусть в момент времени тело находилось в точке с радиус-вектором

Спустя малый промежуток времени тело оказалось в точке с
радиус-вектором

Перемещение тела:

(1)

Мгновенная скорость в момент времени — это предел отношения перемещения к интервалу времени , когда величина этого интервала стремится к нулю; иными словами, скорость точки — это производная её радиус-вектора:

(2)

Из (2) и (1) получаем:

Коэффициенты при базисных векторах в пределе дают производные:

(Производная по времени традиционно обозначается точкой над буквой.) Итак,

Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:

Когда стремится к нулю, точка приближается к точке и вектор перемещения разворачивается в направлении касательной. Оказывается, что в пределе вектор направлен точно по касательной к траектории в точке . Это и показано на рис. 3.

Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна , а спустя малый интервал скорость стала равна .
Ускорение — это предел отношения изменения скорости к интервалу , когда этот интервал стремится к нулю; иначе говоря, ускорение — это производная скорости:

Ускорение, таким образом, есть «cкорость изменения скорости». Имеем:

Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):

Закон сложения скоростей.

Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим и будем называть неподвижной.
Вторая система отсчёта, обозначаемая , связана с телом отсчёта , которое движется относительно тела со скоростью . Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы перемещаются параллельно самим себе (нет вращения системы координат), так что вектор можно считать скоростью движущейся системы относительно неподвижной.

Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью , это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта .

Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью . Муха переносится вагоном, и потому скорость движущейся системы относительно неподвижной называется переносной скоростью.

Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе ) обозначается и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
— радиус-вектор точки в неподвижной системе ;
— радиус-вектор точки в движущейся системе ;
— радиус-вектор тела отсчёта в неподвижной системе .

Рисунок 4.

Как видно из рисунка,

Дифференцируя это равенство, получим:

(3)

(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки в системе , то есть абсолютная скорость:

.

Аналогично, производная есть скорость точки в системе , то есть относительная скорость:

А что такое ? Это скорость точки в неподвижной системе, то есть — переносная скорость движущейся системы относительно неподвижной:

В результате из (3) получаем:

Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.

Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!

Виды механического движения.

Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).

Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.

А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.

В терминах вектора скорости можно дать более короткие определения данным типам движения:

• равномерное движение
• прямолинейное движение
• равномерное прямолинейное движение

Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:

• равноускоренное движение

Наряду с материальной точкой в механике рассматривается ещё одна идеализация — твёрдое тело.
Твёрдое тело — это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.

Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).

Рисунок 5.

Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.

На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.

Рисунок 6.

Перемещение и путь при равноускоренном прямолинейном движении 🐲 СПАДИЛО.РУ

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

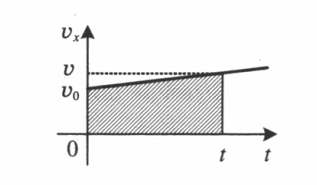
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения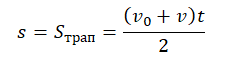

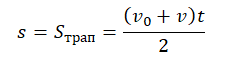
Пример №1. По графику определить перемещение тела в момент времени t=3 с.

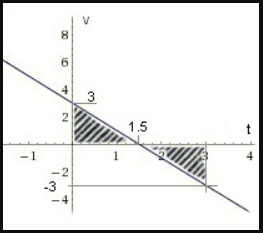
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

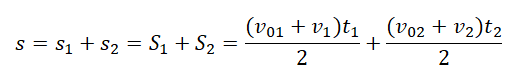
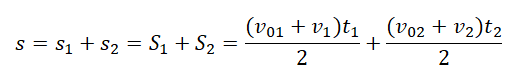
Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀ ± at

В итоге получается формула:

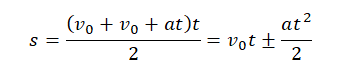
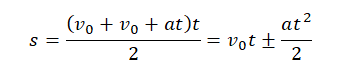
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

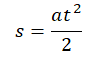
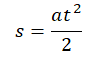
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

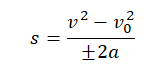
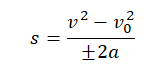
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

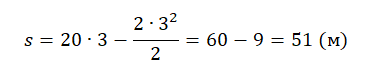
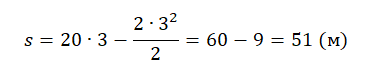
Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

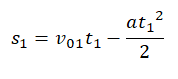
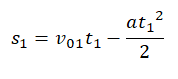
Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

v = at₂

При разгоне перемещение s₂ равно:

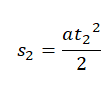
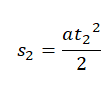
При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

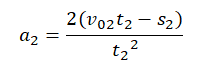
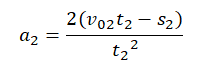
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁ = 0)

Подставляем выраженные величины в формулу:

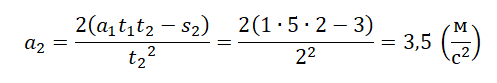
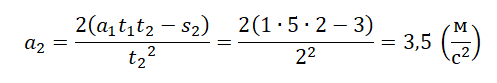
Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

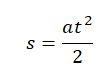
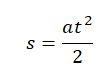
За первую секунду тело переместится на расстояние, равное:

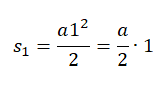
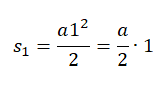
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

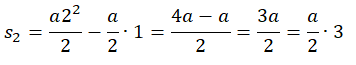
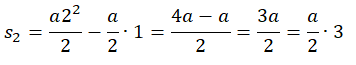
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

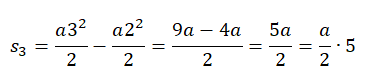
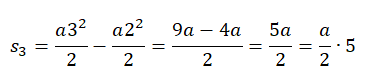
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду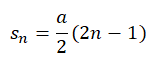

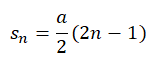
Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

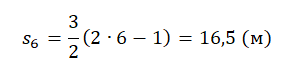
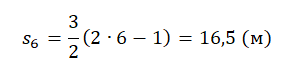
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

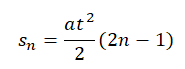
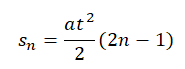
где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

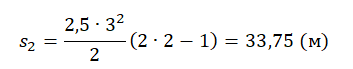
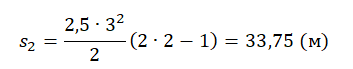
Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

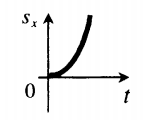
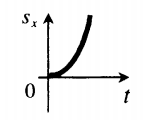
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

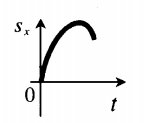
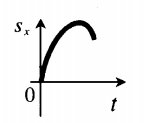
Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

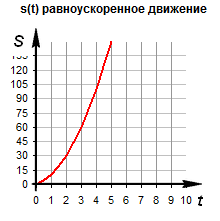
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

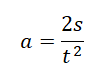
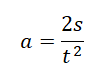
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

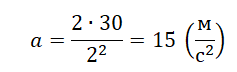
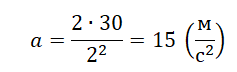
График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

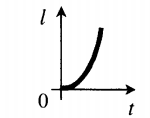
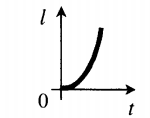
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

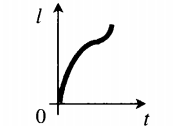
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

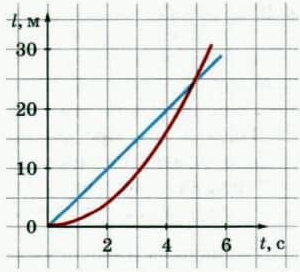
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

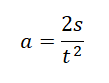
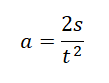
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

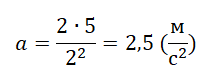
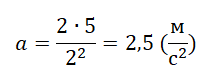Задание EF18831 На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t₁=20 с до t₂=50 с.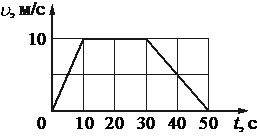

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

Исходные данные:

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s = s₁ + s₂

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

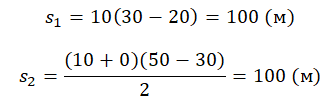
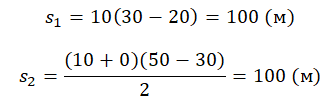
s₁+ s₂= 100 + 100 = 200 (м)

Ответ: 200

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18774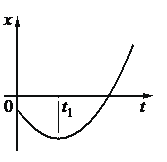

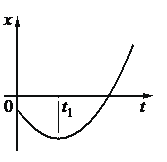
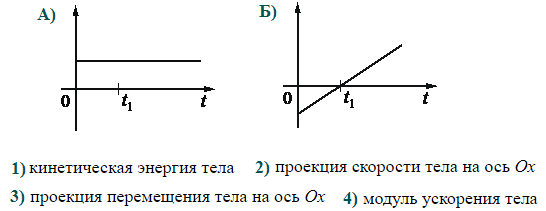
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

• перемещение и путь;
• скорость;
• ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор | оценить

Механическое движение и его характеристики 🐲 СПАДИЛО.РУ

Определения

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

• Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
• Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
• Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.

По типу линии, вдоль которой движется тело, выделяют два вида движения:

• Прямолинейное — тело движется по прямой линии.
• Криволинейное — тело движется по кривой линии, в том числе замкнутой.

По скорости выделяют два вида движения:

• Равномерное — скорость движущегося тела остается неизменной.
• Неравномерное — скорость движущегося тела с течением времени меняется.

По ускорению выделяют три вида движения:

• Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
• Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
• Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

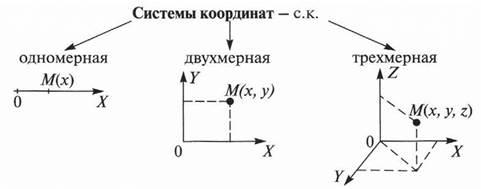
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

• Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
• Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
• Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.

Способы описания механического движения

Описать механическое движение можно двумя способами:

1. координатным
2. векторным

Координатный способ

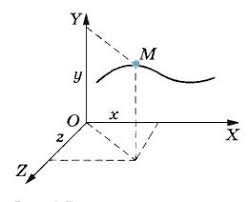
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

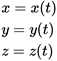
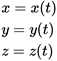
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

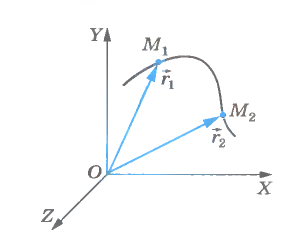
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

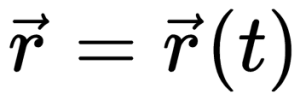
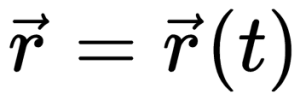
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

1. перемещение
2. скорость
3. ускорение

Перемещение

Определение

Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S.

Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δr. С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:

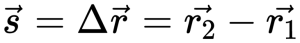
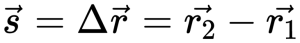
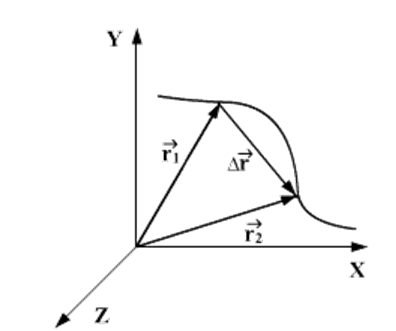
Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

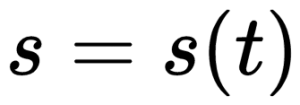
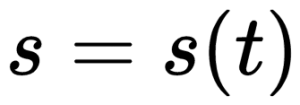
Модуль перемещения — длина вектора перемещения. Обозначается как |Δr|. Единица измерения — метры (м).

Внимание!

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

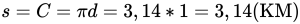
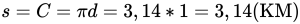
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

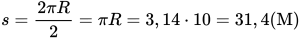
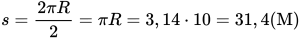
Скорость

Определение

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

В физике скорость обозначается V. Математически скорость определяется формулой:

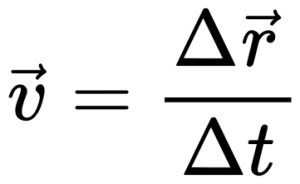
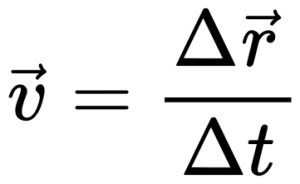
Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

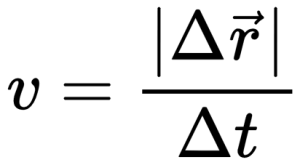
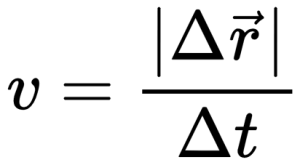
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

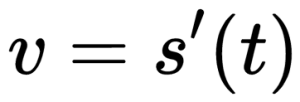
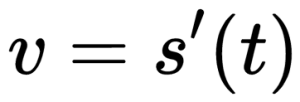
Ускорение

Определение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

В физике ускорение обозначается a. Математически оно определяется формулой:

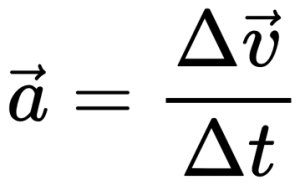
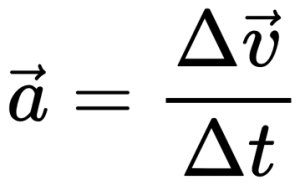
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с²).

Математическое определение модуля скорости:

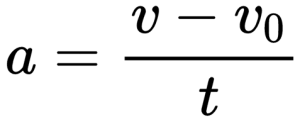
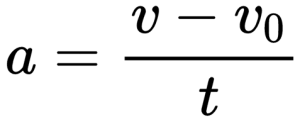v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

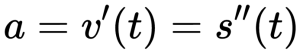
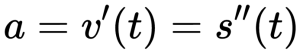
Проекция вектора перемещения на ось координат

Определение

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

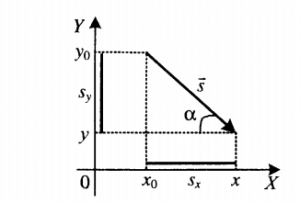
Проекция вектора на ось OX:

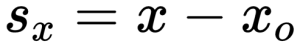
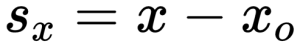
Проекция вектора на ось OY:

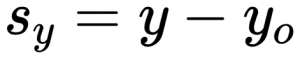
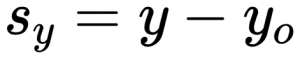
Знаки проекций перемещения

• Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
• Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.

Внимание!

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

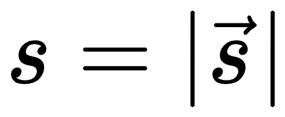
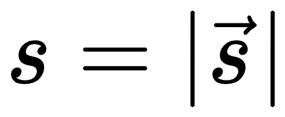
Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

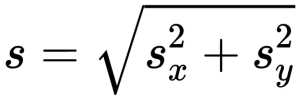
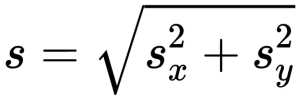
Выразив проекции вектора перемещения через координаты, эта формула примет вид:

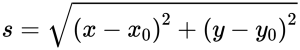
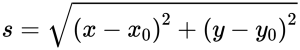
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

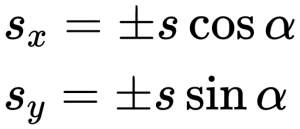
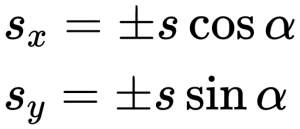
Общий вид уравнений координат:

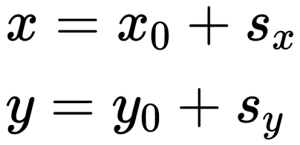
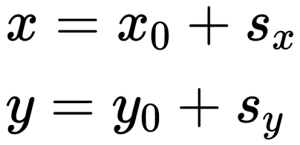
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

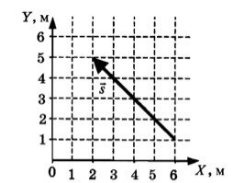
Определяем координаты начальной точки вектора:

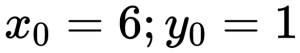
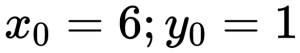
Определяем координаты конечной точки вектора:

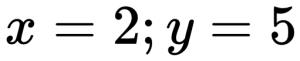
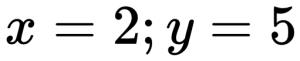
Проекция вектора перемещения на ось OX:

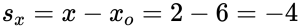
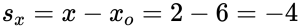
Проекция вектора перемещения на ось OY:

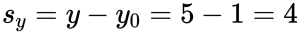
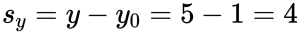
Применяем формулу для вычисления модуля вектора перемещения:

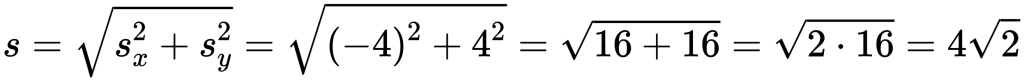
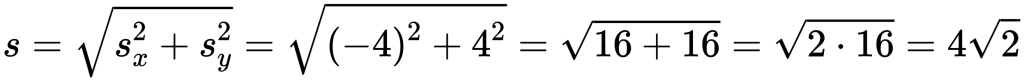
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

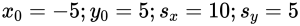
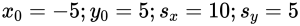
Для определения координаты точки В понадобятся формулы:

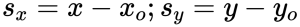
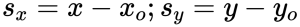
Выразим из них координаты конечного положения точки:

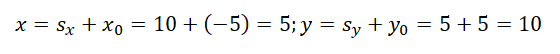
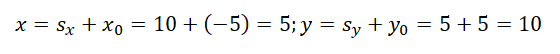
Точка В имеет координаты (5; 10).

Задание EF17612 Тело начинает двигаться из состояния покоя с ускорением 4 м/с². Через 2 с его скорость будет равна…

Алгоритм решения

1. Записать исходные данные в определенной системе отсчета.
2. Записать формулу ускорения.
3. Выразить из формулы ускорения скорость.
4. Найти искомую величину.

Решение

Записываем исходные данные:

• Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v₀ = 0 м/с.
• Ускорение, с которым тело начинает движение, равно: a = 4 м/с².
• Время движения согласно условию задачи равно: t = 2 c.

Записываем формулу ускорения:

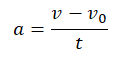
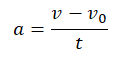
Так как начальная скорость равна 0, эта формула принимает вид:

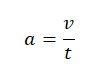
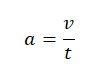
Отсюда скорость равна:

v = at

Подставляем имеющиеся данные и вычисляем:

v = 4∙2 = 8 (м/с)

Ответ: 8

pазбирался: Алиса Никитина | обсудить разбор | оценить

Возможные перемещения — Лекции и примеры решения задач технической механики

Возможными (виртуальными) перемещениями несвободной механической системы называются воображаемые, бесконечно малые перемещения точек системы, допускаемые наложенными на систему связями.

Возможные перемещения – это величины первого порядка малости, величинами высших порядков малости пренебрегаем, поэтому криволинейные перемещения точек заменяются прямолинейными отрезками, откладываемыми в направлении касательной к траектории каждой точки.

Возможные перемещения обозначаются символом «δ». Например, δφ, δS (рисунок 2.1), для точки A:

δS_A = AA’ = OAδφ.

Рисунок 2.1

Все силы, действующие на точки несвободной механической системы, могут быть разделены на задаваемые силы и реакции связей. Задаваемые силы выражают действие на механическую систему тел, не входящих в данную систему. Реакции связей выражают действие связей, ограничивающих движение системы (рисунок 2.2).

Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называют идеальными, т.е.

∑R_i ⋅ δS_i ⋅ cosα_i= 0.

Рисунок 2.2

На рисунке 2.2 при перемещении тела на величину δS (возможное перемещение) работа реакции для гладкой поверхности связи:

δA=N⋅ δS⋅ cos90^o =0

т.е. эта связь идеальна. В случае шероховатой поверхности появляется сила трения и полная реакция такой поверхности будет

R = N + F_ТР

Работа этих двух сил уже не равна нулю.

δA = F_ТР⋅ δS⋅ cos180^o.

Чтобы выведенные в механике принципы можно было применять в реальных задачах, нужно неидеальные связи искусственно сделать идеальными, отнеся силы трения к разряду задаваемых сил.

Принцип виртуальных перемещений >>

Путь и перемещение: что это и чем они отличаются?

Если брать во внимание физические процессы в бытовой сфере, то многие из них кажутся очень погожими. Поэтому понятия путь и перемещение воспринимаются как одно и то же, разница заключается только в том, что первое – это описание действия, а второе – это результат действия. Но если обратиться за уточнением к информационным источникам можно будет сразу же найти существенную разницу между данными операциями.

Что собой представляет путь?

Путь – это движение в результате, которого происходит изменение места расположения предмета или человека. Эта величина относится к скалярным, поэтому не имеет направления, но с её помощью можно определить пройденное расстояние.

Путь может выполняться следующими образами:

• По прямой линии.
• Криволинейно.
• По кругу.
• Возможны другие способы (например, зигзагообразная траектория).

Путь никогда не может быть отрицательным и убывать в течение времени. Измерение пути осуществляется в метрах. Чаще всего, в физике для обозначения пути используется буква S, в редких случаях используют букву L. С помощью пути нельзя предвидеть, где будет находиться нужный нам предмет в определённый момент времени.

Особенности перемещения

Перемещение – это разность между начальной и конечной точкой расположения человека или предмета в пространстве после того как был преодолён какой-то путь.

Значение перемещения всегда является положительным, а также имеет чёткое направление.

Совпадение между перемещением и путём возможно только в том случае если путь был осуществлён по прямой линии, а направление при этом не изменялось.

С помощью перемещения можно рассчитать, где находился человек или предмет в определённый этап времени.

Для обозначения перемещения используют букву S, но поскольку перемещение является векторной величиной то над данной буквой ставится стрелочка →, которая и указывает на то, что перемещение – это вектор. К сожалению, увеличивает путаницу между путём и перемещением ещё тот факт, что оба понятия также можно обозначить буквой L.

Что общего между понятиями путь и перемещение?

Несмотря на то что путь и перемещение – это абсолютно разные понятия существуют определённые элементы, которые способствуют тому, что понятия путают:

1. Путь и перемещение всегда могут быть только положительными величинами.
2. Для обозначения пути и перемещения может использоваться одна и та самая буква L.

Даже учитывая факт, что у этих понятий имеется только два общих элемента их значение настолько велико, что заставляет путаться многих людей. Особенно возникают проблемы у школьников во время изучения физики.

Основные отличия между понятиями путь и перемещение?

У данных понятий имеется ряд отличий, которые всегда помогут определить, какая величина находиться перед вами, путь или перемещение:

1. Путь – это первичное понятие, а перемещение вторичное. К примеру, перемещение определяет разницу между начальной и конечной точкой расположения человека в пространстве после преодоления какого-то пути. Соответственно, нельзя получить величину перемещения не использовав изначально путь.
2. Для пути играет огромную роль начало движения, а для определения перемещения начало движения абсолютно не нужно.
3. Основная разница между данными величинами заключается в том, что путь не имеет направления, а у перемещения оно имеется. К примеру, путь осуществляется только прямо – вперёд, а перемещение допускает и движение назад.
4. Кроме того, понятия отличаются по виду. Путь относится к скалярной величине, а перемещение к векторной.
5. Метод исчисления. К примеру, путь исчисляют с помощью общего пройденного отрезка, а перемещение, в свою очередь, исчисляется с помощью изменения места расположения объекта в пространстве.
6. Путь никогда не может быть равен нулю, а в перемещении допускается значение равное нулю.

Изучив эти отличия, можно сразу же понять в чём заключается разница между понятиями путь и перемещение, и уже больше никогда их не путать.

Разница между путём и перемещением на примерах

Для того чтобы быстрее понять разницу между путём и перемещением можно использовать определённые примеры:

1. Машиной было совершено движение на 2 метра вперёд и на 2 метра назад. Путь – это сумма всего пройденного расстояния, соответственно она составляет 4 метра. А перемещение – это начальная и конечная точка, поэтому в данном случае оно равно нулю.
2. К тому же разницу между путём и перемещением можно рассмотреть на собственном опыте. Необходимо встать на старт 400-метровой беговой дорожки и пробежать два круга (второй круг закончится в начальной точке). В результате получается, что путь составил 800 метров (400+400), а перемещение равно 0, поскольку начальная и конечная точки совпадают.
3. Брошенный вверх мячик достиг высоты в 15 метров, а затем упал на Землю. В данном случае путь будет равен 30 метров, поскольку плюсуются 15 метров вверх и 15 метров вниз. А перемещение будет равно 0, из-за того, что мячик вернулся в исходное положение.

Проанализировав эти примеры, даже люди с гуманитарным складом ума смогут без проблем понять разницу между данными величинами, а при необходимости даже решать задачи, связанные с ними.

Главное, никогда не забывать, что путь и перемещение – это абсолютно разные вещи, даже, несмотря на схожее обозначение. У данных наблюдается такое количество отличий, что перепутать их очень сложно.

Равномерное прямолинейное движение – FIZI4KA

1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.

Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.

2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.

Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.

Если за время ​\( t \)​ тело совершило перемещение ​\( \vec{s} \)​, то скорость его движения ​\( \vec{v} \)​ равна ​\( \vec{v}=\frac{\vec{s}}{t} \)​.

Единица скорости: \( [\,v\,]=\frac{[\,s\,]}{[\,t\,]} \); \( [\,v\,]=\frac{1\,м}{1\,с}=1\frac{м}{с} \). За единицу скорости принимается 1 м/с — скорость такого равномерного движения, при котором тело за 1 с совершает перемещение 1 м.

Зная скорость равномерного движения, можно найти перемещение за любой промежуток времени: \( \vec{s}=\vec{v}t \). Вектор скорости и вектор перемещения направлены в одну сторону — в сторону движения тела.

3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.

Пусть \( \vec{s} \) — перемещение тела (рис. 11). Направим координатную ось ОХ по направлению перемещения. Найдем проекцию перемещения на координатную ось ОХ. На рисунке ​\( x_0 \)​ — координата начальной точки перемещения, ​\( x \)​ — координата конечной точки перемещения. Проекция перемещения равна разности координат конечной и начальной точек: ​\( \vec{s}_x=x-x_0 \)​. С другой стороны, проекция перемещения равна проекции скорости, умноженной на время, т.е. \( \vec{s}_x=\vec{v}_xt \). Откуда ​\( x-x_0=\vec{v}_xt \)​ или \( x=x_0+\vec{v}_xt \). Если начальная координата ​\( x_0 \)​ = 0, то ​\( x=\vec{v}_xt \)​.

Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.

Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае ​\( x>x_0 \)​. Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае \( x<x_0 \).

4. Зависимость координаты от времени можно представить графически.

Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: ​\( x \)​ = 4 м/с · ​\( t \)​. Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).

Для того чтобы её построить, необходимо иметь две точки: одна из них ​\( t \)​ = 0 и ​\( x \)​ = 0, а другая ​\( t \)​ = 1 с, ​\( x \)​ = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.

Если в начальный момент времени координата тела ​\( x_0 \)​ = 2 м, а проекция его скорости ​\( v_x \)​ = 4 м/с, то уравнение движения имеет вид: ​\( x \)​ = 2 м + 4 м/с · ​\( t \)​. Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой ​\( t \)​ = 0, ​\( x \)​ = 2 м (рис. 14).

В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \)​ = 2 м – 4 м/с · ​\( t \)​. График зависимости координаты такого движения от времени представлен на рисунке 15.

Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.

График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.

5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.

Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.

При решении задачи целесообразно придерживаться следующей последовательности действий:

1. Кратко записать условие задачи.
2. Проанализировать ситуацию, описанную в условии задачи:
   — выяснить, можно ли принять движущиеся тела за материальные точки;
   — сделать рисунок, изобразив на нём векторы скорости;
   — выбрать систему отсчёта — тело отсчёта, направления координатных осей, начало отсчёта координат, начало отсчёта времени; записать начальные условия (значения координат в начальный момент времени) для каждого тела.
3. Записать в общем виде уравнение движения в векторной форме и для проекций на координатные оси.
4. Записать уравнение движения для каждого тела с учётом начальных условий и знаков проекций скорости.
5. Решить задачу в общем виде.
6. Подставить в формулу значения величин и выполнить вычисления.
7. Проанализировать ответ.

Применим эту последовательность действий к приведённой выше задаче.

Дано: ​\( v_1 \)​ = 15 м/с  ​\( v_2 \) ​= 12 м/с  ​\( l \) ​= 270 м. Найти: ​\( t \)​ – ?   \( x\)​ – ?

Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь

Система отсчёта связана с Землёй, ось ​\( Ox \)​ направлена в сторону движения первого тела, начало отсчёта координаты — т. ​\( O \)​ — положение первого тела в начальный момент времени.

Начальные условия: ​\( t \)​ = 0; ​\( x_{01} \)​ = 0; \( x_{02} \) = 270.

Уравнение в общем виде: ​\( \vec{s}=\vec{v}t \)​; ​\( x=x_0+v_xt \).

Уравнения для каждого тела с учётом начальных условий: ​\( x_1=v_1t \)​; ​\( x_2=l-v_2t \)​. В месте встречи тел ​\( x_1=x_2 \); следовательно: ​\( v_1t=l-v_2t \)​. Откуда ​\( t=\frac{l}{v_1+v_2}\cdot t \)​. Подставив значение времени в уравнение для координаты первого автомобиля, получим значение координаты места встречи автомобилей: ​\( x \)​ = 150 м.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ​\( v_1 \)​ и скорости «Пежо» — \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ​\( v_1 \)​ и \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м
2) 40 м
3) 80 м
4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​\( v_1 \)​, \( v_2 \) и \( v_3 \) движения этих тел.

1) ​\( v_1=v_2=v_3 \)​
2) \( v_1>v_2>v_3 \)​
3) \( v_1<v_2<v_3 \)​
4) ​\( v_1=v_2 \), \( v_3<v_1 \)

8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​\( x=1t \)​ (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Ответы

Равномерное прямолинейное движение

4.5 (90%) 4 votes

Лучшие способы справиться с небольшим движением

Не каждый ход — большой шаг. Например, тем, кто переезжает в общежитие колледжа или просто на улицу, может не понадобиться помощь грузчиков с полным спектром услуг. Если вы перевозите небольшую партию вещей, возможно, вам удастся уйти, используя собственный автомобиль или службу доставки для перевозки предметов. Чтобы узнать, как справиться с небольшим ходом, ознакомьтесь с нашими советами ниже.

Какие несколько примеров малого хода?

• Переезд в общежитие колледжа — Хотя уход из дома в первый раз, безусловно, может быть огромным, количество вещей на буксире не должно быть слишком большим.На самом деле переезд в комнату в общежитии колледжа — прекрасный пример небольшого переезда. В большинстве комнат общежития колледжа есть кровать, письменный стол, книжная полка и кухонная техника, а это значит, что вам не придется беспокоиться об упаковке и доставке крупногабаритной мебели. Вместо этого вам нужно будет принести только небольшие предметы, такие как постельное белье, школьные принадлежности, туалетные принадлежности и одежду. Вот список того, что взять с собой в колледж.
• Переезд студии или квартиры с одной спальней — Если вы переезжаете в студию или квартиру с одной спальней, то ваш переезд обычно считается небольшим.Это особенно актуально, если вы планируете приобрести мебель и доставить ее после переезда. Переехать в небольшую квартиру означает перевезти только небольшой грузовик с ящиками и мебелью. Обычно это можно сделать, просто арендовав грузовик или грузовой фургон.
• Переезд, не связанный с переездом в новый район — Переезд по улице? Даже если вы планируете привезти с собой домашнее имущество, вы можете считать переезд «небольшим» из-за легкости и удобства передвижения поблизости.Это особенно актуально при перемещении в пределах одного района. Слово мудрым: эти небольшие локальные переезды часто требуют больше времени для завершения. Причина? Домовладельцы, как правило, перемещают вещи отдельными этапами в течение длительного периода времени, что увеличивает продолжительность переезда. Самый эффективный способ совершить небольшой локальный ход — это сразу все вырубить.
• Перемещение только специальных предметов — Маленькие перемещения часто включают удаление одного или двух больших предметов из дома.Примеры предметов, которые обычно отправляются отдельно от других, включают пианино, бильярдный стол, бытовую технику, ценные произведения искусства и ванну — и это лишь некоторые из них. Часто эти предметы может перевезти только транспортная компания, которая специализируется на упаковке и перемещении предметов. Например, в США есть несколько транспортных компаний, занимающихся перемещением пианино (и только пианино). Если вы решили самостоятельно перевезти особый предмет, обязательно прочтите инструкции и внимательно следуйте им.

5 способов справиться с небольшим ходом

1. Наем транспортной компании, специализирующейся на небольших переездах
   

   Самый простой (хотя и самый дорогой) способ справиться с небольшим переездом — это нанять профессиональных грузчиков, которые сделают за вас тяжелую работу.Местные переезды, переезд студий и небольших квартир, а также переезды по специальности — все это происходит более эффективно, если задействована профессиональная транспортная компания. Если вам кажется, что для вашего небольшого переезда нет необходимости в найме транспортной компании с полным спектром услуг, но вы все равно хотите нанять помощников, попробуйте привлечь только рабочих, которые помогут с подъемом. Если вам нужна помощь в перемещении только одного или двух крупных предметов, наймите специализированную транспортную компанию, которая занимается исключительно перемещением вашего конкретного предмета (например, пианино, электроприборов и т. Д.). Вы также можете найти грузчиков, которые специализируются только на небольших движениях.

2. Аренда подвижного контейнера
   

   Аренда небольшого движущегося контейнера — один из лучших способов справиться с небольшим переездом. Если вы перемещаете вещи в небольшую квартиру, перемещаемый контейнер стандартного размера должен быть достаточно большим, чтобы вместить все предметы. Эти движущиеся контейнеры также могут быть особенно полезны для тех, кто переезжает в городскую среду, где места мало и требуется хранение. Поскольку движущиеся контейнеры служат также в качестве единиц хранения, их можно использовать в течение нескольких месяцев для хранения вещей при уменьшении размера до меньшего размера.Чтобы получить помощь в поиске движущегося контейнера, который соответствует вашим потребностям и бюджету, проверьте здесь.

3. Самостоятельное передвижение на автомобиле
   

   Часто переезд в общежитие колледжа означает перемещение только вагона (или двух) вещей. Если небольшой шаг можно сделать, просто загрузив предметы в машину, мы рекомендуем сначала попробовать этот метод. Это не только самый дешевый способ передвижения, но и дает вам максимальную гибкость при выборе графика движения.Используя для передвижения собственный автомобиль, вы полностью контролируете процесс движения от начала до конца и можете двигаться по своему собственному графику.

4. Перемещение на арендованном небольшом грузовике, грузовом фургоне или прицепе
   

   Небольшие переезды обычно можно выполнить с помощью арендованного небольшого грузовика, грузового фургона или прицепа. Аренда небольших грузовиков обычно позволяет переехать с одной или двумя спальнями. Аренда трейлеров и грузовых фургонов идеально подходит для переезда в студию или общежитие колледжа, которые обычно не связаны с крупными предметами мебели.При аренде грузовика, фургона или прицепа обычно также можно арендовать движущееся оборудование (например, тележку или движущиеся ремни). Так что, если вам нужна аренда движущегося оборудования, то аренда движущегося грузовика может убить двух зайцев одним выстрелом. Для получения дополнительной информации и скидок в различных компаниях по аренде грузовиков, таких как Penske, U-Pack и Budget, посетите центр аренды грузовиков Moving.com.

5. Отправления по отдельности
   

   Переезжаете на большие расстояния? Часто лучший способ справиться с небольшим переездом — просто доставить мебель и коробки в новый дом.Если вы решили отправить небольшой груз, есть несколько способов сделать это. Для более крупных товаров рекомендуется обратиться к партнерам по доставке на uShip.com. Веб-сайт позволяет легко найти поставщика услуг, который может организовать для вас доставку специальных товаров. Что касается коробок и других различных предметов, рассмотрите возможность доставки их через USPS, UPS или FedEx. Имейте в виду, что эти почтовые службы часто имеют определенные правила и ограничения по размеру и весу отправлений, которые могут быть отправлены.

Что следует учитывать при перемещении небольшого груза

Перед тем, как выбрать способ перемещения ваших предметов, необходимо учесть несколько важных моментов.К ним относятся:

• Состояние ваших вещей — Планируете ли вы перевезти хрупкие фужеры, зеркала или телевизоры? Потребуются ли ваши вещи при перемещении? Если это так, то, вероятно, бросать какие-то предметы в заднюю часть машины не удастся. Вместо этого рассмотрите возможность найма профессионалов, которые помогут с процессом упаковки и погрузки. Если вы решили переехать самостоятельно, арендуйте грузовик с соответствующими креплениями, чтобы предметы не смещались во время транспортировки.
• Ваш график движения — У вас есть все время в мире, чтобы двигаться? Даже небольшой переезд может занять недели, если не месяцы.Если у вас достаточно времени, чтобы завершить переезд, и вы предпочитаете делать это поэтапно, то использование собственного автомобиля или арендованного фургона имеет смысл. Однако, если вам нужно, чтобы переезд был завершен за один день или в выходные, возможно, имеет смысл нанять профессионалов, которые сделают это.
• Расстояние движения — Как далеко вы двигаетесь? При перемещении на большие расстояния имеет смысл либо отправить вещи в новый дом, либо нанять профессиональных грузчиков, чтобы они отвезли вещи к месту назначения.Если вы двигаетесь поблизости, вы можете передвигаться на автомобиле или арендованном грузовике.
• Ваши потребности в хранении — Вам нужно место для хранения вещей до, во время или после переезда? Аренда небольшого движущегося контейнера, вероятно, является лучшим вариантом для успешного переезда. Эти контейнеры служат также в качестве единиц хранения, поэтому вам не придется беспокоиться о поиске места для самостоятельного хранения при переезде в новый дом.
• Ваше время и энергия — У вас есть время и энергия, чтобы справиться с небольшим переездом без помощи профессионалов? Если вы способны справиться с тяжелой работой самостоятельно, тогда неплохая идея — сделать самодельный переезд, взяв напрокат грузовик или личный автомобиль.Если, с другой стороны, у вас нет времени или энергии, чтобы справиться с переездом, то правильным выбором может быть найм профессионалов.
• Ваш бюджет — В конечном итоге, то, как вы переедете, будет во многом зависеть от того, что вы можете себе позволить. Тем, у кого ограниченный бюджет, стоит подумать об использовании собственного автомобиля или аренды грузовика на день. Те, у кого более гибкий бюджет, могут подумать о найме специалиста или аренде движущегося контейнера.

Предпочитаете нанять профессиональных грузчиков, чтобы справиться с вашим небольшим переездом?

Не у всех есть время и силы, чтобы совершить переезд, даже самый маленький.К счастью, существует множество профессиональных транспортных компаний, которые могут справиться с этой задачей за вас. Чтобы найти лучшую транспортную компанию для перевозки ваших вещей, проверьте обширную сеть надежных и уважаемых перевозчиков Moving.com. Все компании по переезду в нашей сети имеют лицензии и застрахованы, поэтому вы можете быть уверены, что ваш небольшой переезд будет в надежных руках. Удачи и счастливого переезда!

.

определение движения по The Free Dictionary

В течение последних двух ходов как для игроков, так и для зрителей было очевидно, что Гахан двигался прямо через поле во вражескую страну в поисках личного сражения с Оранжевым вождем — что он делал ставку на свою веру в превосходство своей власти. владеть фехтованием, поскольку, если два вождя вступают в бой, исход игры решает.

Если вы не можете указать это движение слева направо, двигаясь в нем, то я умоляю вас описать его мне словами.

Другими словами, вместо того, чтобы всегда двигаться в направлении одной из своих конечностей, вы никогда не испытываете желания двигаться в направлении, так сказать, своей стороны?

Они движутся, чтобы есть, чтобы двигаться дальше. Вот и все: они не устают и не пропускают шаг, не падают в ряд и не опускаются на обочину, чтобы их оставили созерцать движущуюся процессию. Несвицкий оглянулся и увидел в пятнадцати шагах от них, но разделенных живой массой. из движущейся пехоты Васька Денисов, рыжий и косматый, в фуражке на затылке и в плаще, беспечно свисающем через плечо.«Думаю, что да», — пробормотал мэр провинции; и, нахмурив брови, он впал в интроспективное состояние, его губы шевелились, как у человека, повторяющего мистические слова. Ни для вас, ни для кого-либо другого нет ничего, что великие огни парламентского неба не помогли в этом деле за несколько лет. чтобы показать вам пример движения вперед. «Господи!» он сказал себе — и снова это было так, как если бы кто-то высказал свою мысль, — «если эти люди такие, какими я их принимаю, мы проиграли битву, и они продвигаются к Нэшвиллу!» Подобный сюрприз может быть сделан перемещать вещи, когда группа спешит и не может остаться, чтобы сознательно обдумать, что перемещается.Опустив голову перед собой и борясь с ветром, который стремился сорвать с него покрывало, Левин подходил к рощице и только что увидел что-то белое за дубом, как вдруг вспыхнула вспышка: вся земля казалась в огне, и небесный свод, казалось, рушился над головой. Сделав это и привязав его к железной корке в передней части саней, где он был раньше, он обошел конюшню, чтобы положить затвор и накрыть его тряпкой, но в этот момент он заметил, что в санях что-то движется, и голова Никиты поднялась из снега, покрывшего ее..

Пример сглаживания скользящей средней | solver

В этом примере показано, как использовать метод сглаживания скользящих средних XLMiner для выявления тенденций во временных рядах, содержащих сезонность. На ленте XLMiner на вкладке Применение вашей модели выберите Справка — Примеры , затем Примеры прогнозирования / анализа данных и откройте набор данных в качестве примера, Airpass.xlsx . Этот набор данных содержит ежемесячное количество пассажиров международных авиакомпаний за 1949-1960 годы.

После открытия набора данных примера щелкните ячейку в наборе данных, затем на ленте XLMiner на вкладке Time Series выберите Partition , чтобы открыть диалоговое окно Time Series Partition Data .

Выберите месяц в качестве переменной времени и пассажиров в качестве переменных в данных раздела . Щелкните OK , чтобы разделить данные на наборы для обучения и проверки. (Разбиение на разделы необязательно. Методы сглаживания могут выполняться для полных неразмеченных наборов данных.)

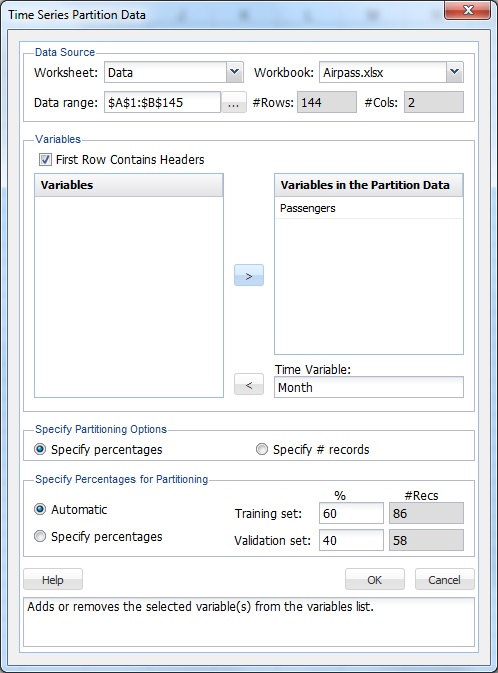
Щелкните рабочий лист Data_PartitionTS, , затем на ленте XLMiner на вкладке Временной ряд выберите Сглаживание — скользящее среднее , чтобы открыть диалоговое окно Сглаживание скользящего среднего .

Месяц уже выбран в качестве переменной времени. Выберите «Пассажиры» в качестве выбранной переменной. Поскольку ожидается, что этот набор данных будет включать некоторую сезонность (т. Е. Количество пассажиров авиакомпаний увеличивается в праздничные и летние месяцы), значение параметра Interval — weight должно быть длиной одного сезонного цикла (т.э., 12 месяцев). В результате введите 12 в поле «Интервал» и выберите «Производить прогноз при проверке».

Щелкните OK , чтобы применить метод сглаживания к секционированному набору данных.

Два листа, MASmoothingOutput и MASmoothing_Stored , вставляются сразу справа от рабочего листа Data_PartitionTS . Дополнительные сведения о листе MASmoothing_Stored см. В разделе «Применение модели — оценка новых данных».

Щелкните рабочий лист MASmoothingOutput . График фактического и реального времени. Диаграммы прогноза (данные обучения) и (данные проверки) показывают, что метод сглаживания скользящего среднего не дает хорошего соответствия, поскольку модель не эффективно отражает сезонность в наборе данных. Летние месяцы, когда количество авиапассажиров обычно велико, по всей видимости, занижены, а в месяцы, когда количество авиапассажиров невелико, модель дает слишком высокий прогноз.Прогноз скользящего среднего никогда не следует использовать, если набор данных включает сезонность. Альтернативой может быть выполнение регрессии модели, а затем применение этого метода к остаткам.

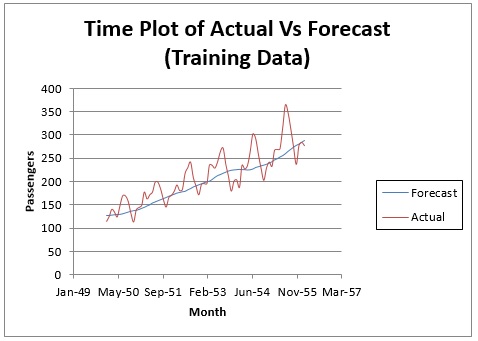
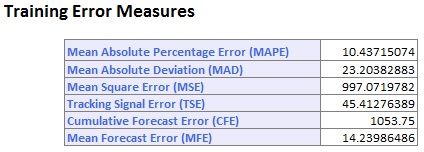
Следующий пример не учитывает сезонность. На ленте XLMiner на вкладке Применение модели выберите Справка — Примеры , затем выберите Примеры прогнозирования / интеллектуального анализа данных и откройте пример набора данных Доход.xlsx . Этот набор данных содержит средний доход налогоплательщиков по штатам. Сначала разделите набор данных на наборы для обучения и проверки, используя год в качестве переменной времени и CA в качестве переменных в данных раздела.

Щелкните OK , чтобы принять значения по умолчанию для разделения и создать наборы для обучения и проверки. Рабочий лист Data_PartitionTS вставляется сразу справа от рабочего листа Income .

Щелкните рабочий лист Data_PartitionTS , затем на ленте XLMiner на вкладке Time Series выберите Smoothing — Moving Average , чтобы открыть диалоговое окно Moving Average Smoothing .Год был автоматически выбран в качестве переменной времени. Выберите CA в качестве выбранной переменной и в разделе «Параметры вывода» выберите «Создать прогноз».

Щелкните OK , чтобы запустить метод сглаживания скользящего среднего. Два листа, MASmoothingOutput и MASmoothing_Stored , вставлены справа от рабочего листа Data_PartitionTS . Для получения дополнительной информации о рабочем листе MASmoothing_Stored см. Раздел Применение вашей модели — Оценка новых данных.

Результаты метода сглаживания скользящей средней на этом наборе данных показывают гораздо лучшее соответствие.

.

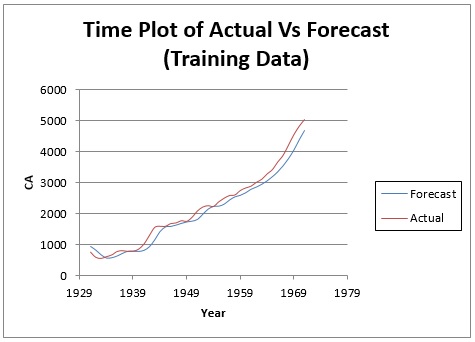
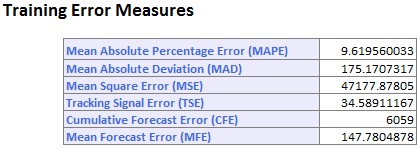
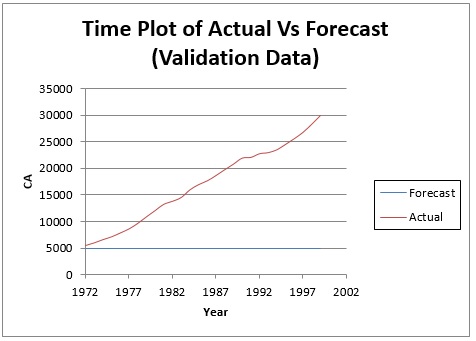
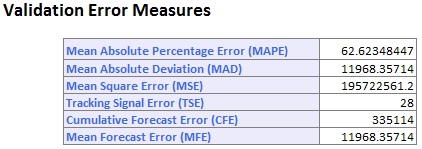
Примеры конвекции

Конвекция возникает, когда тепло передается через газ или жидкость более горячим материалом, движущимся в более прохладную зону.

• В метеорологии это передача тепла и других атмосферных свойств за счет движения масс воздуха, особенно в восходящем направлении.

Конвекция в метеорологии и геологии

• Мантийная конвекция — скалистая мантия Земли движется медленно из-за конвективных токов, которые переносят тепло из недр Земли на поверхность.Это причина того, что тектонические плиты постепенно перемещаются вокруг Земли. Горячий материал добавляется к растущим краям тарелки, а затем охлаждается. На краях потребления материал становится плотным из-за сжатия под воздействием тепла и опускается в Землю в океанической впадине. Это вызывает образование вулканов.

• Океанская циркуляция — теплая вода вокруг экватора циркулирует к полюсам, а более холодная вода на полюсах движется к экватору.

• Эффект стека — также называемый эффектом дымохода, это движение воздуха внутрь и наружу из зданий, дымоходов или других объектов из-за плавучести.В этом случае плавучесть относится к разной плотности воздуха между воздухом внутри и воздухом снаружи. Сила плавучести увеличивается из-за большей высоты конструкции и большей разницы между уровнем тепла внутреннего и внешнего воздуха.

• Конвекция звезды — звезда имеет зону конвекции, в которой энергия перемещается за счет конвекции. За пределами активной зоны находится зона излучения, в которой движется плазма. Конвекционный ток образуется, когда плазма поднимается, а остывшая плазма опускается.

• Гравитационная конвекция — показывает, когда сухая соль диффундирует вниз во влажную почву, потому что пресная вода в соленой воде обладает плавучестью.

Вот примеры:

• Кондиционирование воздуха

• Центральное отопление

• Паровые турбины

• Теплообменники

• Аэродинамический обогрев

с использованием пропеллеров

автомобиля

• жидкость

• Кровообращение у теплых окровавленных животных

• Ударные волны, исходящие от взрыва

• Конвекционная печь

Эти различные примеры конвекции показывают, как конвекция возникает во многих различных искусственных и природных места где.

Примеры конвекции.