Метод изображений — Карта знаний
- Метод изображений (метод зеркальных отображений) — один из методов математической физики, применяемый для решения краевых задач для уравнения Гельмгольца, уравнения Пуассона, волнового уравнения и некоторых других.
Суть метода изображений состоит в том, что исходная задача отыскания поля заданных (сторонних) источников в присутствии граничных поверхностей сводится к расчёту поля тех же и некоторых добавочных (фиктивных) источников в безграничной среде, которые помещаются вне области отыскания поля исходной задачи. Эти добавочные источники называются источниками-изображениями. Правила их построения полностью аналогичны тем, по которым строятся изображения точечных источников в оптике в системе зеркал (здесь зеркала повторяют форму граничных поверхностей). Величины источников-изображений определяются граничными условиями на поверхностях, а также требованиями одинаковости поля, создаваемого реальной системой источников и поверхностей, и системой, составленной из действительных источников и фиктивных источников-изображений в пространстве вблизи действительных источников.
С помощью метода изображений обычно решаются задачи, в которых каждому заданному точечному источнику можно сопоставить конечную систему (иногда бесконечный дискретный ряд) однотипных точечных источников-изображений. Поэтому наибольшее распространение метод изображений получил в электростатике. Также метод изображений можно распространить на более широкий класс границ и граничных условий в рамках метода геометрической оптики при достаточно малой длине волны и некоторых уточняющих его коротковолновых приближений. В этом случае он сводится к построению картины лучей и геометрооптических изображений.
Справедливость метода зеркальных отображений доказывается с помощью теоремы единственности решения соответствующего дифференциального уравнения (уравнения Пуассона в случае электростатики) при определённых граничных условиях.
В электростатике метод позволяет легко рассчитать распределение электрического поля в объёме между совокупностью электрических зарядов и проводящими поверхностями определённой формы, а также между электрическими зарядами и диэлектрическими поверхностями. В простейшем случае, когда электрический заряд расположен над проводящей плоскостью (рис. 1), электрическое поле между зарядом и поверхностью является идентичным полю между этим зарядом и его противоположно заряженным зеркальным отображением. Обоснованность такой замены вытекает из условия отсутствия тангенциальной составляющей вектора напряжённости электрического поля на поверхности проводника, или, другими словами, вытекает из того, что потенциал поля одинаков в любой точке проводящей поверхности. Отсюда также очевидно, что сила взаимодействия между зарядом и плоскостью равна силе взаимодействия между фактическим зарядом и его зеркальным отображением, а также то, что эта сила взаимодействия является силой притяжения.
Аналогично метод зеркальных отображений позволяет рассчитать магнитное поле постоянных токов, находящихся над проводящей или диэлектрической плоскостью.
Кроме того, в магнитостатике метод позволяет рассчитать магнитное поле в объёме между совокупностью магнитных диполей (или каким-либо источником внешнего магнитного поля) и поверхностью идеального сверхпроводника (см. эффект Мейснера). Здесь, в простейшем случае магнитного диполя над сверхпроводящей плоскостью (рис. 2), поле от экранированных сверхпроводящих токов вне сверхпроводника является эквивалентным полю отражённого диполя. Обоснованность вытекает из условия отсутствия нормальной составляющей магнитного поля на поверхности сверхпроводника. Сила взаимодействия между магнитом и идеальным сверхпроводником является отталкивающей. Существует также обобщение метода — метод застывших зеркальных изображений, который применим также и к сверхпроводникам с сильным пинингом.
Метод часто используют для расчёта других полей, например потоков жидкости или тепла.
Источник: Википедия
Связанные понятия
Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил её (см. ниже). Уравнение, представляющее собой содержание теоремы в этом обобщённом виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей — то есть в принципе в магнитостатике — верна теорема в первоначальном виде, сформулированном…
Магнитоста́тика — раздел классической электродинамики, изучающий взаимодействие постоянных токов посредством создаваемого ими постоянного магнитного поля и способы расчета магнитного поля в этом случае. Под случаем магнитостатики или приближением магнитостатики понимают выполнение этих условий (постоянства токов и полей — или достаточно медленное их изменение со временем), чтобы можно было пользоваться методами магнитостатики в качестве практически точных или хотя бы приближенных. Магнитостатика…
Бетатронные колебания — быстрые поперечные колебания, совершаемые частицей в фокусирующих магнитных полях ускорителя. Бетатронные колебания — основной предмет изучения электронной оптики, раздела физики ускорителей.
Электростатика (др. -греч. ήλεκτρον — янтарь) — раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов.
Сфера Лоренца — метод вычисления локального поля в микроскопической теории диэлектриков. Позволяет найти диэлектрическую проницаемость материала, если известна дипольная поляризуемость частиц материала. Широкую известность получил после выхода в свет классического труда Хендрика Антона Лоренца «Теория электронов и её применение к явлениям света и теплового излучения».
Мультипо́ли (от лат. multum — много и греч. πόλος — полюс) — определённые конфигурации точечных источников (зарядов). Простейшими примерами мультиполя служат точечный заряд — мультиполь нулевого порядка; два противоположных по знаку заряда, равных по абсолютной величине — диполь, или мультиполь 1-го порядка; 4 одинаковых по абсолютной величине заряда, размещённых в вершинах параллелограмма, так что каждая его сторона соединяет заряды противоположного знака (или два одинаковых, но противоположно направленных…
Подробнее: Мультиполь
Дипо́ль — идеализированная система, служащая для приближённого описания поля, создаваемого более сложными системами зарядов, а также для приближенного описания действия внешнего поля на такие системы. Дипольное приближение, выполнение которого обычно подразумевается, когда говорится о поле диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка. Полученные функции будут эффективно…
Ковариа́нтный метод — подход в теоретической физике, разработанный Ф. И. Фёдоровым на основе линейной алгебры и прямого тензорного исчисления. Получил распространение в приложении к описанию оптических явлений и, частично, в физике элементарных частиц.
Диакоптика, или метод Крона (англ. diakoptics, греческий dia-через, усиливает слово, стоящее за ним и может интерпретировано как «система» + kopto-разрыв) — один из методов расчленения при исследовании сложных систем, которые могут быть представлены в виде блок-схемы или графа с использованием граф-топологического портрета системы как нового источника информацииТермин диакоптика использовал Крон в серии статей «Diakoptics — The Piecewise Solution of Large-Scale Systems», опубликованных между 7 июня…
Фотоны, которые мигрируют в биологических тканях могут быть описаны при помощи численного моделирования методом Монте Карло или аналитическим уравнением переноса излучения (УПИ). Однако, УПИ трудно решается без применения упрощений (приближений). Стандартным методом упрощения УПИ является диффузионное приближение. Общее решение уравнения диффузии для фотонов получается быстрее, но менее точно чем методом Монте Карло.
Подробнее: Диффузионное приближение УПИ в тканях
Соотноше́ния Кра́мерса — Кро́нига — интегральная связь между действительной и мнимой частями любой комплексной функции, аналитичной в верхней полуплоскости. Часто используются в физике для описания связи действительной и мнимой частей функции отклика физической системы, поскольку аналитичность функции отклика подразумевает, что система удовлетворяет принципу причинности, и наоборот . В частности, соотношения Крамерса — Кронига выражают связь между действительной и мнимой частями диэлектрической проницаемости…
Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость…
Подробнее: Силовые линии векторного поля
Главным образом, интерес к вопросу распространения волн в случайно-неоднородных средах (какой является, например, атмосфера) можно объяснить бурным развитием спутниковых технологий. В этом случае становится важной задача расчета характеристик (например, амплитуды) волны прошедшей через среду и установления их связей с параметром неоднородности среды. Важную роль здесь и играет функция Грина для случайно-неоднородной среды, зная которую можно определить эти характеристики. Рассматривается прохождение…
Подробнее: Функция Грина для случайно-неоднородной среды
Физические свойства графена проистекают из электронных свойств атомов углерода и поэтому часто имеют нечто общее с остальными аллотропными модификациями углерода, которые были известны до него, такими как графит, алмаз, углеродные нанотрубки. Конечно, схожести больше с графитом, так как он состоит из графеновых слоёв, но без новых уникальных физических явлений и исследований других материалов и наработок физических методов анализа и теоретических подходов графен не привлёк бы специалистов из таких…
Фазовое пространство в математике и физике — пространство, каждая точка которого соответствует одному и только одному состоянию из множества всех возможных состояний системы. Точка пространства, соответствующая состоянию системы называется «изображающей» или «представляющей» для него. Таким образом, изменению состояний системы, — т.е. её динамике — можно сопоставить движение изображающей точки; траекторию этой точки называют фазовой траекторией (следует отметить, что она не тождествлена действительной…
Оптико-механическая аналогия — аналогия между описаниями движения материальных частиц в стационарном потенциальном поле в классической механике и распространения движения световых лучей в изотропной оптически неоднородной среде. Была установлена Гамильтоном в 1834 г. В 1926 г. была использована при создании квантовой механики де Бройлем и Шредингером для описания наличия у материальных объектов одновременно корпускулярных и волновых свойств.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке.
Функции Бриллюэна и Ланжевена представляют собой пару специальных функций , которые появляются при изучении идеализированного парамагнитного материала в статистической механике.
В теории поля представление системы зарядов в виде некоторых квадрупо́лей, аналогично представлению её в виде системы диполей, используется для приближённого расчёта создаваемого ей поля и излучения. Более общим представлением является разложение системы на мультиполи, соответствующее разложению потенциалов в ряд Тейлора по некоторым переменным. Квадруполь — частный случай мультиполя. Квадрупольное рассмотрение системы оказывается особенно важным в том случае, когда её дипольный момент и заряд равны…
Подробнее: Квадруполь
Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела.
Ве́кторная диагра́мма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.
Электромагни́тное взаимоде́йствие — одно из четырёх фундаментальных взаимодействий. Электромагнитное взаимодействие существует между частицами, обладающими электрическим зарядом. С современной точки зрения электромагнитное взаимодействие между заряженными частицами осуществляется не прямо, а только посредством электромагнитного поля.
Теория Линдхард — метод расчета эффекта экранировки электрического поля электронами в твердом теле. Он базируется на квантовой механике (первый порядок теории возмущений) в пpиближении случайной фазы.
Квантова́ние Дира́ка — эвристический аргумент, предложенный П. Дираком и показывающий, что однозначность предсказаний квантовой механики с электрическими зарядами может быть сохранена в теории, включающей магнитные монополи, лишь при условии совместного квантования магнитного и электрического зарядов.
Теория потенциала — раздел математики и математической физики, посвящённый изучению свойств дифференциальных уравнений в частных производных в областях с достаточно гладкой границей посредством введения специальных видов интегралов, зависящих от определённых параметров, называемых потенциалами.
Радиационное трение, реакция излучения, лучистое трение, торможение излучением — сила, действующая на заряженную точечную частицу (например, электрон), со стороны её собственного электромагнитного излучения, вызываемого неравномерностью движения этой частицы.
Магни́тный монопо́ль — гипотетическая элементарная частица, обладающая ненулевым магнитным зарядом — точечный источник радиального магнитного поля. Магнитный заряд является источником статического магнитного поля совершенно так же, как электрический заряд является источником статического электрического поля.
Тео́рия упру́гости — раздел механики сплошных сред, изучающий деформации упругих твёрдых тел, их поведение при статических и динамических нагрузках.
Вращательная диффузия — процесс, при котором устанавливается или поддерживается равновесное статистическое распределение энергии по вращательным степеням свободы ансамбля частиц или молекул. Вращательная диффузия (диффузия вращения) является аналогом обычной (трансляционной) диффузии.
Спин-орбитальное взаимодействие — в квантовой физике взаимодействие между движущейся частицей и её собственным магнитным моментом, обусловленным спином частицы. Наиболее часто встречающимся примером такого взаимодействия является взаимодействие электрона, находящегося на одной из орбит в атоме, с собственным спином. Такое взаимодействие, в частности, приводит к возникновению так называемой тонкой структуры энергетического спектра электрона и расщеплению спектроскопических линий атома.
Теоре́ма И́рншоу — теорема об электростатическом поле, сформулирована в XIX веке английским физиком Ирншоу в 1842 году.
То́чечный заря́д — идеализация, вводимая для упрощения описания поля заряженного тела или системы тел. Иногда также определяется как электрически заряженная материальная точка.
Эффе́кт Шта́рка — смещение и расщепление электронных термов атомов во внешнем электрическом поле.
Метод ренормализационной группы (также часто называемый методом ренормгруппы, методом РГ) в квантовой теории поля — итеративный метод перенормировки, в котором переход от областей с меньшей энергией к областям с большей вызван изменением масштаба рассмотрения системы.
Подробнее: Ренормализационная группа
Магнитосопротивление (магниторезистивный эффект) — изменение электрического сопротивления материала в магнитном поле. Впервые эффект был обнаружен в 1856 Уильямом Томсоном. В общем случае можно говорить о любом изменении тока через образец при том же приложенном напряжении и изменении магнитного поля. Все вещества в той или иной мере обладают магнетосопротивлением. Для сверхпроводников, способных без сопротивления проводить электрический ток, существует критическое магнитное поле, которое разрушает…
Подробнее: Магнетосопротивление
Атом гелия — это атом химического элемента гелия. Гелий состоит из двух электронов привязанных электромагнитной силой к ядру, которое содержит два протона вместе с одним или двумя нейтронами, в зависимости от изотопа, удерживаемые вместе сильным взаимодействием. В отличие от водорода, замкнутой формы решения уравнения Шредингера для атома гелия не найдено. Однако, различные приближения, такие, как метод Хартри–Фока, можно использованы для оценки энергии основного состояния и волновой функции атома…
Ква́нтовая тео́рия по́ля (КТП) — раздел физики, изучающий поведение квантовых систем с бесконечно большим числом степеней свободы — квантовых (или квантованных) полей; является теоретической основой описания микрочастиц, их взаимодействий и превращений. Именно на квантовой теории поля базируется вся физика высоких энергий, физика элементарных частиц и физика конденсированного состояния. Квантовая теория поля в виде Стандартной модели (с добавкой масс нейтрино) сейчас является единственной экспериментально…
Критическая динамика — раздел теории критического поведения и статистической физики, описывающий динамические свойства физической системы в или вблизи критической точки. Является продолжением и обобщением критической статики, позволяя описывать величины и характеристики системы, которые нельзя выразить лишь через одновременны́е равновесные функции распределения. Такими величинами являются, например, коэффициенты переноса, скорости релаксации, разновременны́е корреляционные функции, функции отклика…
Квантовая теория рассеяния — раздел квантовой механики, описывающий рассеяние частиц на изолированном рассеивающем центре. В простейшем случае, этот центр характеризуется потенциалом. Обычно предполагается, что потенциал стремится к нулю по мере удаления от рассеивающего центра.
Магнети́зм — форма взаимодействия движущихся электрических зарядов, осуществляемая на расстоянии посредством магнитного поля. Наряду с электричеством, магнетизм — одно из проявлений электромагнитного взаимодействия. С точки зрения квантовой теории поля электромагнитное взаимодействие переносится бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля).
Уравнение синус-Гордона — это нелинейное гиперболическое уравнение в частных производных в 1 + 1 измерениях, включающее в себя оператор Даламбера и синус неизвестной функции. Изначально оно было рассмотрено в XIX веке в связи с изучением поверхностей постоянной отрицательной кривизны. Это уравнение привлекло много внимания в 1970-х из-за наличия у него солитонных решений.
Уровни Ландау — энергетические уровни заряженной частицы в магнитном поле. Впервые получены как решение уравнения Шрёдингера для заряженной частицы в магнитном поле Л. Д. Ландау в 1930 году. Решением этой задачи являются волновые функции электрона в гармоническом потенциале. Уровни Ландау играют существенную роль во всех кинетических явлениях в присутствии магнитного поля.
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917-го года.
Квадрупо́льная ли́нза — устройство для фокусировки пучков заряженных частиц с помощью магнитного или реже электрического поля квадрупольной конфигурации.
В квантовой механике, частица в одномерном периодическом потенциале — это идеализированная задача, которая может быть решена точно (при некоторых специального вида потенциалах), без упрощений. Предполагается, что потенциал бесконечен и периодичен, то есть обладает трансляционной симметрией, что, вообще говоря, не выполняется для реальных кристаллов, и всегда существует как минимум один дефект — поверхность (это приводит к другой задаче о поверхностных состояниях или таммовских уровнях).
Обменное взаимодействие — взаимодействие тождественных частиц в квантовой механике, приводящее к зависимости значения энергии системы частиц от её полного спина. Представляет собой чисто квантовый эффект, исчезающий при предельном переходе к классической механике.
Блочный Гамильтониан — гамильтониан, описывающий критическое поведение магнетика вблизи точки фазового перехода второго рода.
Ниже приведены примеры уравнений непрерывности, которые выражают одинаковую идею непрерывного изменения некоторой величины. Уравнения непрерывности — (сильная) локальная форма законов сохранения.
Подробнее: Уравнение непрерывности
Ква́нтовый эффе́кт Хо́лла в графене или необы́чный ква́нтовый эффе́кт Хо́лла — эффект квантования холловского сопротивления или проводимости двумерного электронного газа или двумерного дырочного газа в сильных магнитных полях в графене. Этот эффект был предсказан теоретически и подтверждён экспериментально в 2005 году.
Метод изображений — это… Что такое Метод изображений?
Метод изображений (метод зеркальных отображений) — один из методов математической физики, применяемый для решения краевых задач для уравнения Гельмгольца, уравнения Пуассона, волнового уравнения и некоторых других.
Суть метода изображений состоит в том, что исходная задача отыскания поля заданных (сторонних) источников в присутствии граничных поверхностей сводится к расчёту поля тех же и некоторых добавочных (фиктивных) источников в безграничной среде, которые помещаются вне области отыскания поля исходной задачи. Эти добавочные источники называются источниками-изображениями. Правила их построения полностью аналогичны тем, по которым строятся изображения точечных источников в оптике в системе зеркал (здесь зеркала повторяют форму граничных поверхностей). Величины источников-изображений определяются граничными условиями на поверхностях, а также требованиями одинаковости поля, создаваемого реальной системой источников и поверхностей, и системой, составленной из действительных источников и фиктивных источников-изображений в пространстве вблизи действительных источников.
С помощью метода изображений обычно решаются задачи, в которых каждому заданному точечному источнику можно сопоставить конечную систему (иногда бесконечный дискретный ряд) однотипных точечных источников-изображений. Поэтому наибольшее распространение метод изображений получил в электростатике. Также метод изображений можно распространить на более широкий класс границ и граничных условий в рамках метода геометрической оптики при достаточно малой длине волны и некоторых уточняющих его коротковолновых приближений. В этом случае он сводится к построению картины лучей и геометрооптических изображений.
Пример 1: Точечный заряд и проводящая плоскость
Пусть точечный заряд расположен на расстоянии от проводящей плоскости. Требуется определить силу, с которой плоскость действует на заряд.
Введём равный и противоположный по знаку заряд-изображение с другой стороны плоскости на том же расстоянии. Сила притяжения между реальным зарядом зарядом-изображением определяется по закону Кулона:
Пример 2: Точечный заряд вблизи границы раздела двух диэлектриков
Справедливость метода зеркальных отображений доказывается с помощью теоремы единственности решения соответствующего дифференциального уравнения (уравнения Пуассона в случае электростатики) при определённых граничных условиях.
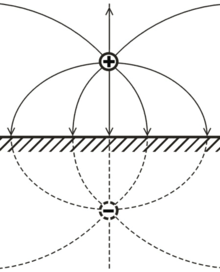
Рис. 1. Положительный заряд над проводящей плоскостью и его отображение. Показаны лини электрического поля.
В электростатике метод позволяет легко рассчитать распределение электрического поля в объёме между совокупностью электрических зарядов и проводящими поверхностями определённой формы, а также между электрическими зарядами и диэлектрическими поверхностями. В простейшем случае, когда электрический заряд расположен над проводящей плоскостью (Рис. 1), электрическое поле между зарядом и поверхностью является идентичным полю между этим зарядом и его противоположно заряженным зеркальным отображением. Обоснованность такой замены вытекает из условия отсутствия тангенциальной составляющей вектора напряжённости электрического поля на поверхности проводника, или, другими словами, вытекает из того, что потенциал поля одинаков в любой точке проводящей поверхности[1]. Отсюда также очевидно, что сила взаимодействия между зарядом и плоскостью равна силе взаимодействия между фактическим зарядом и его зеркальным отображением, а также то, что эта сила взаимодействия является силой притяжения.
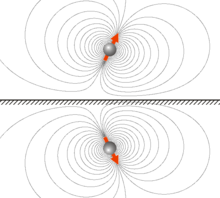
Рис. 2. Магнитный диполь над поверхностью идеального сверхпроводника и его отображение. Показаны линии индуцированного ими магнитного поля.
Аналогично метод зеркальных отображений позволяет рассчитать магнитное поле постоянных токов, находящихся над проводящей или диэлектрической плоскостью.
Кроме того, в магнитостатике метод позволяет рассчитать магнитное поле в объёме между совокупностью магнитных диполей (или каким-либо источником внешнего магнитного поля) и поверхностью идеального сверхпроводника (см. эффект Мейснера). Здесь, в простейшем случае магнитного диполя над сверхпроводящей плоскостью (Рис. 2), поле от экранированных сверхпроводящих токов вне сверхпроводника является эквивалентным полю отражённого диполя. Обоснованность вытекает из условия отсутствия нормальной составляющей магнитного поля на поверхности сверхпроводника. Сила взаимодействия между магнитом и идеальным сверхпроводником является отталкивающей. Существует также обобщение метода — метод застывших зеркальных отображений (англ.), который применим также и к сверхпроводникам с сильным пинингом.
Метод часто используют для расчёта других полей, например потоков жидкости или тепла.[2]
Ссылки
Литература
- Купалян С. Д. Теоретические основы электротехники, ч. 3, Электромагнитное поле. М., 1970.
- Бессонов Л. А. Теоретические основы электротехники, Изд-во «Высшая школа», 1967.
Примечания
- ↑ Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 5: Электричество и магнетизм. Перевод с английского (издание 3). — Эдиториал УРСС. — ISBN 5-354-00703-8
- ↑ AllPhysics.ru: Электростатические аналогии
§ 10. Метод электростатических изображений
В теории электромагнетизма доказано, что решение корректно поставленных задач единственно. Существует наглядный метод нахождения поля, удовлетворяющего условиям задачи, называемый методом изображений.
Его суть состоит в следующем. Поле точечного заряда хорошо известно. Стараются подобрать такую систему точечных зарядов, суммарное поле которых удовлетворяет всем условиям задачи. Из теоремы об единственности решения заключаем, что это поле дает искомое решение. Математически задача сводиться к нахождению потенциала, удовлетворяющего условиям задачи. Напряженность Е направлена перпендикулярно эквипотенциальным поверхностям и вычисляется как взятый с обратным знаком градиент от потенциала. Получить форму эквипотенциальных поверхностей системы точечных зарядов в принципе легко.
Фактически сказанное означает, что если нарисовать картину силовых линий поля, создаваемого системой заряженных объектов, и она совпадает с картиной силовых линий поля, создаваемого системой точечных зарядов, то это означает, что эти поля одинаковы. И сложный расчет поля в первом случае изменяется на довольно простой во втором. Еще раз отметим, что в графической интерпретации это означает, что у этих полей одинаковая картина силовых линий.
Пример 1.
Дана проводящая бесконечная плоскость и заряд q > 0 на расстоянии r от плоскости. Найти поле в точке М.

 На плоскости будут индуцироваться заряды с плотностью
На плоскости будут индуцироваться заряды с плотностью 
 М, согласно принципу суперпозиции, равен
М, согласно принципу суперпозиции, равен
 . (10.1)
. (10.1)
Отметим, что сам потенциал проведенной плоскости будет равен 0.
Если строго решать эту задачу, необходимо найти закон распределения

 и вычислить
и вычислить 
 в точке М, а затем воспользоваться принципом суперпозиции (10.1).
в точке М, а затем воспользоваться принципом суперпозиции (10.1).
Рассмотрим поле, создаваемое двумя точечными зарядами +q и –q, расположенными на расстоянии 2r друг от друга.


Если провести плоскость, перпендикулярную линии 2R, то это будет эквипотенциальная поверхность, как легко видеть, с потенциалом, равным 0.
Картина силовых линий справа на двух рисунках одинакова. Значит «действие» бесконечной отрицательно заряженной плоскости совместно с положительным точечным зарядом +q справа от эквипотенциальной поверхности может быть заменено на «действие», обусловленное двумя точечными зарядами +q и –q, находящимися на расстоянии 2R. В этом случае можно считать, что поле в первом случае создается зарядом q и его «изображением» –q, «как в зеркале».
Следовательно, можно заключить, что потенциал поля в точке М во втором случае

 . Но тогда этой же формулой можно представить потенциал поля в точке М в первом случае, если ввести понятие изображения заряда q в плоскости, как в зеркале, т. е. заряд –q – фиктивный заряд, который называется изображением заряда q в плоскости. Не нужно решать никакую сложную задачу, а поле в точке М находится как суперпозиция полей заряд q и его изображения –q.
. Но тогда этой же формулой можно представить потенциал поля в точке М в первом случае, если ввести понятие изображения заряда q в плоскости, как в зеркале, т. е. заряд –q – фиктивный заряд, который называется изображением заряда q в плоскости. Не нужно решать никакую сложную задачу, а поле в точке М находится как суперпозиция полей заряд q и его изображения –q.
Сила взаимодействия между зарядом q и бесконечной проводящей плоскостью будет равна силе взаимодействия заряда q м его изображения, т. е.

 .
.
Пример 2.
Даны 2 перпендикулярные проводящие полуплоскости и заряд +q. Найти

 .
.
Метод изображений позволяет зразу вычислить поле в точке М. Найдем изображение q в этих плоскостях. Если оптически построить изображение точки +q в двух перпендикулярных зеркалах, то изображений будет три: q1, q2 и q3 – третье изображение из-за переотражений в зеркалах. Очевидно, что q1

 =–q; q
=–q; q
 2=–q, а q
2=–q, а q
 3=–(–q)= q. И тогда потенциал поля в точке М Можно найти как суперпозицию полей заряда q и трех его «изображений». Естественно, количество таких ситуаций ограничено.
3=–(–q)= q. И тогда потенциал поля в точке М Можно найти как суперпозицию полей заряда q и трех его «изображений». Естественно, количество таких ситуаций ограничено.
Метод изображений, конечно, не сводится во всех случаях в буквальном смысле к нахождению зеркального изображения зарядов. В курсе уравнений математической физики метод изображений, например, используется для построения функции точечного источника (функции Грина) I краевой задачи для уравнения Лапласа. Там же мы встречаем изображение на круге, изображение на сфере.
В заключение рассмотрим еще один пример.
Пример 3.

 Определим силу взаимодействия между проводящей заземленной сферой радиуса А и точечным зарядом q2 расположенном на расстоянии d2 от центра сферы и поле этой системы в точке М.
Определим силу взаимодействия между проводящей заземленной сферой радиуса А и точечным зарядом q2 расположенном на расстоянии d2 от центра сферы и поле этой системы в точке М.
В этом случае потенциал сферы равен 0.
Рассмотрим сначала поле, создаваемое двумя точечными зарядами q1 и q2, расположенными с точкой О на одной прямой на расстоянии d1 и d2 от точки О.

 .
.
Найдем эквипотенциальную поверхность, удовлетворяющую условию

 . Пусть q1 = | q1|, q2 = — | q2|. Тогда
. Пусть q1 = | q1|, q2 = — | q2|. Тогда
 .
.
Сгруппируем слагаемые следующим образом:

 .
.
Чтобы равенство нулю выполнялось для всех θ, необходимо потребовать:

 .
.
Тогда получим

 ,
, 
 . Подставим q1 в А2:
. Подставим q1 в А2:
 . Следовательно, если
. Следовательно, если 
 , а
, а 
 , то потенциал на воображаемой сфере радиуса А будет равен нулю. Причем
, то потенциал на воображаемой сфере радиуса А будет равен нулю. Причем 
 .
.
Теперь проведем сопоставление исходной задачи и рассмотренного примера. В обоих случаях имеется сфера с потенциалом равным нулю. Поле в пространстве вне сферы, очевидно, будет одинаково, так как во втором случае тот же заряд и та же сфера. Таким образом, можно сделать следующий вывод:
Если ввести изображение заряда q1 на сфере радиуса А, то этот заряд

 . В этом случае поле, создаваемое сферой и зарядом q2 , будет точно таким же, как поле, создаваемое зарядом q2 и его изображением на сфере q1, т. е. потенциал в точке М:
. В этом случае поле, создаваемое сферой и зарядом q2 , будет точно таким же, как поле, создаваемое зарядом q2 и его изображением на сфере q1, т. е. потенциал в точке М:
 .
.
А сила взаимодействия между проводящей заземленной сферой и зарядом q2 будет определяться законом Кулона как сила взаимодействия между зарядом q2 и его изображением на сфере – зарядом q1, т. е. легко найти, что

 .
.
Kvant. Метод электростат. изображений — PhysBook
Черноуцан А.И. Метод электростатических изображений //Квант. — 1987. — № 3. — С. 39-42.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В школьном курсе физики вы познакомились с явлением электростатической индукции. Вспомним, в чем оно заключается.
Поднесем точечный заряд +q к какому-либо проводнику, например к незаряженному металлическому шарику. За очень малое время свободные заряды на шарике перераспределятся так, что напряженность результирующего поля внутри него станет равной нулю. После этого движение зарядов прекратится. Поле внешнего заряда оказывается скомпенсированным полем зарядов, «появившихся» на поверхности шарика. Будем называть их наведенными зарядами.
Поле наведенных зарядов есть и вне проводника, в частности, оно действует на заряд +q — заряд притягивается к шарику, хотя полный заряд шарика равен нулю (рис. 1, а). Если бы шарик был заземлен, притяжение было бы сильнее, поскольку на шарике появился бы избыточный отрицательный заряд (рис. 1, б). Этот заряд перетек бы на проводник с земли под действием поля заряда +q[1].
а
б
Рис. 1
Как рассчитать поле наведенных зарядов? Рассмотрим пример. Пусть проводник занимает все правое полупространство (рис. 2). Тогда на его плоской границе ОО’ соберутся наведенные отрицательные заряды, которые уничтожат поле всюду в проводнике. Вычислить поле вне проводника (слева от ОО’) нам поможет тот очевидный факт, что поле наведенных зарядов симметрично относительно плоскости ОО’. Посмотрите на рисунок 2 — на нем хорошо видно, чему равно поле наведенных зарядов справа от ОО’ (в проводнике). Раз это поле компенсирует поле заряда +q, то, очевидно, оно совпадает с полем воображаемого заряда —q, помещенного в ту же точку, что и заряд +q. Теперь ясно, какое поле создают наведенные заряды слева от ОО’ (вне проводника). Оно в точности равно полю воображаемого заряда —q, но помещенного по другую сторону от плоскости ОО’, симметрично по отношению к заряду +q. Заряд —q называют изображением заряда +q.
Рис. 2
Итак, плоская поверхность проводника притягивает точечный заряд +q, удаленный от нее на растояние d, с такой же силой, с какой его притягивал бы заряд —q, удаленный на расстояние 2d:
\(~F = k \frac{q^2}{(2d)^2}\) .
Мы получили удивительный результат: поле, создаваемое зарядом и проводником (рис. 3, а), в пространстве вне проводника совпадает с полем всего двух точечных зарядов (рис. 3, б). Почему оказалась возможной такая подмена? Вспомним, что поверхность проводника представляет собой эквипотенциальную поверхность, причем в нашем примере потенциал проводника равен нулю. Поле же двух зарядов +q и —q обладает следующим свойством: эквипотенциальная поверхность φ = 0 совпадает с плоскостью симметрии ОО’, т. е. точно повторяет форму поверхности рассматриваемого проводника. Именно в этом скрыта причина совпадения полей, изображенных на рисунке 3, а и б. И в других случаях надо стремиться расположить заряды-изображения внутри проводника так, чтобы поверхность проводника совпала с поверхностью постоянного потенциала, равного потенциалу проводника[2].
Рис. 3
Возникает резонный вопрос — как это сделать? Как найти заряды-изображения и их положения, если известны форма и потенциал проводника? К сожалению, в общем случае такого рецепта не существует, и обычно приходится действовать, как говорят, «с конца» — от зарядов к проводнику.
Возьмем несколько точечных зарядов, рассчитаем их поле, найдем любую эквипотенциальную поверхность φ = φ0 и заполним пространство внутри этой поверхности проводником с потенциалом φ0. Тогда поле, которое мы уже рассчитали, представляет собой готовое решение для получившегося проводника и тех зарядов, что оказались вне его! Заряды же, которые «погибли» внутри проводника, играют роль зарядов-изображений. Таким способом можно построить много «готовых» решений, но нет гарантии, что среди них найдется проводник заранее заданной формы.
Рассмотрим пример. Возьмем какую-нибудь эквипотенциальную поверхность для тех же зарядов +q и —q, например с φ = -1 В (рис. 4, а). Поле этих двух зарядов вне этой поверхности совпадает с полем заряда +q и проводника, имеющего фиксированный потенциал φ = -1 В (рис. 4, б).
а
б
Рис. 4
Еще пример. Поле четырех зарядов +q, +q, —q и —q, размещенных в вершинах прямоугольника (рис. 5, в), имеет эквипотенциальную поверхность φ = 0 в виде двух взаимно перпендикулярных плоскостей. Значит, часть этого поля, заключенная в первом квадранте, совпадает с полем заряда +q, помещенного в двухгранный угол (рис. 5, б). Три других заряда являются изображениями заряда +q. Попробуйте сами найти решение для заряда, помещенного в трехгранный угол, — для этого вам придется использовать семь дополнительных зарядов.
а
б
Рис. 5
Вернемся теперь к примеру с металлическим шариком, о котором шла речь в начале статьи. Возьмем два заряда +q1 и —q2 (q1 > q2), расположенные на расстоянии l друг от друга. Оказывается, что эквипотенциальная поверхность φ = 0 представляет собой сферу (рис. 6, а)[3]. Чтобы определить радиус этой сферы R и расстояние L от ее центра до заряда +q1 можно приравнять к нулю потенциалы точек А и В (рис. 6, б):
\(~\begin{matrix} k \frac{q_1}{L — R} — k \frac{q_2}{R — (L — l)} = 0 \\ k \frac{q_1}{L + R} — k \frac{q_2}{R + (L — l)} = 0 \end{matrix}\) . (*)
а
б
Рис. 6
Поле этих двух зарядов в пространстве вне сферы в точности совпадает с полем, которое возникает, если заряд +q1 поместить на расстоянии L от центра заземленного металлического шара радиусом R (рис. 6, б). В этом случае, когда задано положение шара, нам известны R и L, а положение отрицательного заряда-изображения (l) и его величину (q2) можно найти из той же системы (*):
\(~\begin{matrix} l = L — \frac{R^2}{L} \\ q_2 = q_1 \frac{R}{L} \end{matrix}\) .
Сила, с которой заряд +q1 притягивается к шару, равна
\(~F = k \frac{q_1 q_2}{l^2}\) .
А как же найти поле и силу притяжения в случае незаряженного шарика? Тогда кроме изображения —q2 надо поместить в центр сферы еще один воображаемый заряд +q2. Поле этих трех зарядов вне сферы будет совпадать с полем заряда +q1 и незаряженного шарика. Почему? Заметим, что поверхность сферы останется эквипотенциальной поверхностью и после добавления третьего заряда. Зато число силовых линий, входящих внутрь сферы, теперь точно равно числу силовых линий, из нее выходящих, — ведь полный заряд внутри сферы равен нулю. Но такому же условию удовлетворяет поле и в случае незаряженного проводника! Значит, мы нашли правильное поле. Сила притяжения заряда +q1 к шару в этом случае будет заметно меньше — ведь он не только притягивается к изображению —q2, но и отталкивается (с меньшей силой) от другого изображения +q2:
\(~F = k \frac{q_1 q_2}{l^2} — k \frac{q_1 q_2}{L^2}\) .
Примечания
- ↑ Поле вне проводника может быть определено, если известен либо полный заряд проводника (как в случае, изображенном на рисунке 1, а), либо его потенциал (как на рисунке 1, б). Первый случай соответствует изолированному проводнику, второй — проводнику, соединенному с удаленным очень большим проводником известного потенциала (например, с землей). Мы, в основном, будем рассматривать второй тип задач. Потенциал бесконечного проводника будем считать равным потенциалу на бесконечности, т. е. нулю.
- ↑ Тогда поле внешних зарядов и проводника будет совпадать с полем внешних зарядов и зарядов-изображений (т. е. проводник подменяется изображениями). Дело в том, что граница рассматриваемой области (пространство вне проводника) имеет в этих двух случаях одинаковый потенциал, и расположение зарядов внутри области также одно и то же (все изображения находятся в проводнике, т. е. вне этой области). Выполнения этих условий достаточно, чтобы утверждать, что поля совпадают всюду внутри области. Это утверждение часто называют принципом единственности в электростатике.
- ↑ Потенциал точечного заряда q имеет вид\[~\varphi = k \frac{q}{r}\]. Условие \(~k \frac{q_1}{r_1} — k \frac{q_2}{r_2} = 0\) преобразуется к равенству \(~\frac{r_1}{r_2} = \frac{q_1}{q_2}\) , т. е. описывает геометрическое место точек, отношение расстояний от которых до заданных двух точек имеет фиксирован иое значение. Докажите сами, что это сфера.
Сегментация изображения / Хабр
Сегментация изображения
Одной из основных задач обработки и анализа изображений является сегментация, т.е. разделение изображения на области, для которых выполняется определенный критерий однородности, например, выделение на изображении областей приблизительно одинаковой яркости. Понятие области изображения используется для определения связной группы элементов изображения, имеющих определенный общий признак (свойство).
Один из основных и простых способов — это построение сегментации с помощью порога. Порог — это признак (свойство), которое помогает разделить искомый сигнал на классы. Операция порогового разделения заключается в сопоставлении значения яркости каждого пикселя изображения с заданным значением порога.
Бинаризация
Операция порогового разделения, которая в результате дает бинарное изображение, называется бинаризацией. Целью операции бинаризации является радикальное уменьшение количества информации, содержащейся на изображении. В процессе бинаризации исходное полутоновое изображение, имеющее некое количество уровней яркости, преобразуется в черно-белое изображение, пиксели которого имеют только два значения – 0 и 1
Пороговая обработка изображения может проводиться разными способами.
Бинаризация с нижним порогом
Бинаризация с нижним порогом
Бинаризация с нижним порогом является наиболее простой операцией, в которой используется только одно значение порога:
Все значения вместо критерия становятся 1, в данном случае 255 (белый) и все значения(амплитуды) пикселей, которые больше порога t — 0 (черный).
Бинаризации с верхним порогом
Иногда можно использовать вариант первого метода, который дает негатив изображения, полученного в процессе бинаризации. Операция бинаризации с верхним порогом:
Бинаризация с двойным ограничением
Для выделения областей, в которых значения яркости пикселей может меняться в известном диапазоне, вводится бинаризация с двойным ограничением (t1<t2):
Так же возможны другие вариации с порогами, где пропускается только часть данных (средне полосовой фильтр).
Неполная пороговая обработка
Данное преобразование дает изображение, которое может быть проще для дальнейшего анализа, поскольку оно становится лишенным фона со всеми деталями, присутствующими на исходном изображении.
Многоуровневое пороговое преобразование
Данная операция формирует изображение, не являющееся бинарным, но состоящее из сегментов с различной яркостью.
Что касается бинаризации, то по сути все. Хотя можно добавить, что есть глобальная, которая используется для всего изображения и так же существует локальная, которая захватывает часть картинки (изображения).
Локальная пороговая обработка
Метод Отса
Метод использует гистограмму распределения значений яркости пикселей растрового изображения. Строится гистограмма по значениям pi=ni/N, где N – это общее кол-во пикселей на изображении, ni – это кол-во пикселей с уровнем яркости i. Диапазон яркостей делится на два класса с помощью порогового значения уровня яркости k,k — целое значение от 0 до L. Каждому классу соответствуют относительные частоты ω0ω1:
Средние уровни для каждого из двух классов изображения:
Далее вычисляется максимальное значение оценки качества разделения изображения на две части:
где (σкл)2=ω0ω1(μ1-μ0)2, – межклассовая дисперсия, а (σобщ)2 – это общая дисперсия для всего изображения целиком.
Определение порога на основе градиента яркости изображения
Предположим, что анализируемое изображение можно разделить на два класса – объекты и фон. Алгоритм вычисления порогового значения состоит из следующих 2 шагов:
1. Определяется модуль градиента яркости для каждого пикселя
изображения
2. Вычисление порога:
Метод использования энтропии гистограммы
Метод приобрел свои различные формы описания и возможные вариации. Распределения общей массы порогов на определенное количество с использованием различных законов и форм распределения.
Глобальная пороговая обработка
Метод Бернсена
1. Обычная квадратная апертура с нечетным числом пикселей пробегает в цикле по всем пикселям исходного изображения. На каждом шаге находится Min и Max.
2. Находится среднее значение Avg= (Min + Max) /2.
3. Если текущий пиксель больше Avg
4. Если среднее меньше порога контраста — то текущий пиксель становится того цвета, который задавался параметром «цвет сомнительного пикселя».
Имеет ряд недостатков: после обработки монотонных областей яркости формируются сильные паразитные помехи, в некоторых случаях приводит к появлению ложных черных пятен
Метод Эйквила
Одним из самых производительных методов является метод Эйквеля. Его часто применяют для обработки четких и контрастных изображений. Согласно данному методу изображение обрабатывается с помощью двух концентрических окон: маленького – S, и большого L. Обычно форма окон принимается квадратной. Оба окна последовательно слева направо сверху вниз накладываются на изображение с шагом равным стороне маленького окна S. Для окна L рассчитывается порог B так, чтобы поделить пиксели на два кластера. Если математические ожидания уровня яркости в двух кластерах имеют разницу, превышающую некоторый заданный пользователем уровень /μ1-μ2/≥l, то все пиксели внутри окна S бинаризуются в соответствии с порогом T. В противном случае, яркость пикселей из окна S заменяется некоторым близким значением.
Метод Ниблэка
Идея данного метода состоит в варьировании порога яркости B бинаризации от точки к точке на основании локального значения стандартного отклонения. Порог яркости в точке (x, y) рассчитывается так:
где μ(x, y) – среднее и s(x, y) — среднеквадратичное отклонение выборки для некоторой окрестности точки. Размер окрестности должен быть минимальным, но таким, чтобы сохранить локальные детали изображения. В то же время размер должен быть достаточно большим, чтобы понизить влияние шума на результат. Значение k определяет, какую часть границы объекта взять в качестве самого объекта. Значение k=-0.2 задает достаточно хорошее разделение объектов, если они представлены черным цветом, а значение k=+0.2, – если объекты представлены белым цветом.
Метод Яновица и Брукштейна
В качестве пороговой поверхности бинаризации используется поверхность потенциалов, строящаяся на основе локальной максимизации градиента яркости. начение градиента яркости часто рассчитывается с помощью контурного оператора Собеля или Кэнни. Изображение фильтруется с целью получения контурных линий толщины в 1 пиксель, а затем усредняющим фильтром 3×3. Потенциальная поверхность, теперь, строится по итерационной интерполирующей схеме. Расчет поверхности идет в порядке, начиная от контурных пикселей. Для каждого не контурного пикселя рассчитывается интерполяционный остаток R(x, y) и новое значение пикселя P(x, y) на n+1-ом шаге должно рассчитываться в соответствии с формулами:
β в пределах 1≤β≤2 для быстрой сходимости.
Итого
Что нашел с радостью выложил вам, в дальнейшем, если получится и будет время, постараюсь реализовать часть алгоритмов. Это лишь малая часть всего, что сегодня существует, но я рад поделится и этим.
Спасибо за внимание.
Пару слов о распознавании образов / Хабр
Давно хотел написать общую статью, содержащую в себе самые основы Image Recognition, некий гайд по базовым методам, рассказывающий, когда их применять, какие задачи они решают, что возможно сделать вечером на коленке, а о чём лучше и не думать, не имея команды человек в 20.
Какие-то статьи по Optical Recognition я пишу давненько, так что пару раз в месяц мне пишут различные люди с вопросами по этой тематике. Иногда создаётся ощущение, что живёшь с ними в разных мирах. С одной стороны понимаешь, что человек скорее всего профессионал в смежной теме, но в методах оптического распознавания знает очень мало. И самое обидное, что он пытается применить метод из близрасположенной области знаний, который логичен, но в Image Recognition полностью не работает, но не понимает этого и сильно обижается, если ему начать рассказывать что-нибудь с самых основ. А учитывая, что рассказывать с основ — много времени, которого часто нет, становится всё ещё печальнее.
Эта статья задумана для того, чтобы человек, который никогда не занимался методами распознавания изображений, смог в течении 10-15 минут создать у себя в голове некую базовую картину мира, соответствующую тематике, и понять в какую сторону ему копать. Многие методы, которые тут описаны, применимы к радиолокации и аудио-обработке.
Начну с пары принципов, которые мы всегда начинаем рассказывать потенциальному заказчику, или человеку, который хочет начать заниматься Optical Recognition:
- При решении задачи всегда идти от простейшего. Гораздо проще повесить на персону метку оранжевого цвета, чем следить за человеком, выделяя его каскадами. Гораздо проще взять камеру с большим разрешением, чем разрабатывать сверхразрешающий алгоритм.
- Строгая постановка задачи в методах оптического распознавания на порядки важнее, чем в задачах системного программирования: одно лишнее слово в ТЗ может добавить 50% работы.
- В задачах распознавания нет универсальных решений. Нельзя сделать алгоритм, который будет просто «распознавать любую надпись». Табличка на улице и лист текста — это принципиально разные объекты. Наверное, можно сделать общий алгоритм(вот хороший пример от гугла), но это будет требовать огромного труда большой команды и состоять из десятков различных подпрограмм.
- OpenCV — это библия, в которой есть множество методов, и с помощью которой можно решить 50% от объёма почти любой задачи, но OpenCV — это лишь малая часть того, что в реальности можно сделать. В одном исследовании в выводах было написано: «Задача не решается методами OpenCV, следовательно, она неразрешима». Старайтесь избегать такого, не лениться и трезво оценивать текущую задачу каждый раз с нуля, не используя OpenCV-шаблоны.
Очень сложно давать какой-то универсальный совет, или рассказать как создать какую-то структуру, вокруг которой можно строить решение произвольных задач компьютерного зрения. Цель этой статьи в структуризации того, что можно использовать. Я попробую разбить существующие методы на три группы. Первая группа это предварительная фильтрация и подготовка изображения. Вторая группа это логическая обработка результатов фильтрации. Третья группа это алгоритмы принятия решений на основе логической обработки. Границы между группами очень условные. Для решения задачи далеко не всегда нужно применять методы из всех групп, бывает достаточно двух, а иногда даже одного.
Список приведённых тут методов не полон. Предлагаю в комментариях добавлять критические методы, которые я не написал и приписывать каждому по 2-3 сопроводительных слова.
Часть 1. Фильтрация
В эту группу я поместил методы, которые позволяют выделить на изображениях интересующие области, без их анализа. Большая часть этих методов применяет какое-то единое преобразование ко всем точкам изображения. На уровне фильтрации анализ изображения не производится, но точки, которые проходят фильтрацию, можно рассматривать как области с особыми характеристиками.
Бинаризация по порогу, выбор области гистограммы
Самое просто преобразование — это бинаризация изображения по порогу. Для RGB изображения и изображения в градациях серого порогом является значение цвета. Встречаются идеальные задачи, в которых такого преобразования достаточно. Предположим, нужно автоматически выделить предметы на белом листе бумаги:
Выбор порога, по которому происходит бинаризация, во многом определяет процесс самой бинаризации. В данном случае, изображение было бинаризовано по среднему цвету. Обычно бинаризация осуществляется с помощью алгоритма, который адаптивно выбирает порог. Таким алгоритмом может быть выбор матожидания или моды. А можно выбрать наибольший пик гистограммы.
Бинаризация может дать очень интересные результаты при работе с гистограммами, в том числе в ситуации, если мы рассматриваем изображение не в RGB, а в HSV . Например, сегментировать интересующие цвета. На этом принципе можно построить как детектор метки так и детектор кожи человека.
Классическая фильтрация: Фурье, ФНЧ, ФВЧ
Классические методы фильтрации из радиолокации и обработки сигналов можно с успехом применять во множестве задач Pattern Recognition. Традиционным методом в радиолокации, который почти не используется в изображениях в чистом виде, является преобразование Фурье (конкретнее — БПФ ). Одно из немногих исключение, при которых используется одномерное преобразование Фурье, — компрессия изображений. Для анализа изображений одномерного преобразования обычно не хватает, нужно использовать куда более ресурсоёмкое двумерное преобразование.
Мало кто его в действительности рассчитывает, обычно, куда быстрее и проще использовать свёртку интересующей области с уже готовым фильтром, заточенным на высокие (ФВЧ) или низкие(ФНЧ) частоты. Такой метод, конечно, не позволяет сделать анализ спектра, но в конкретной задаче видеообработки обычно нужен не анализ, а результат.
Самые простые примеры фильтров, реализующих подчёркивание низких частот (фильтр Гаусса) и высоких частот (Фильтр Габора).
Для каждой точки изображения выбирается окно и перемножается с фильтром того же размера. Результатом такой свёртки является новое значение точки. При реализации ФНЧ и ФВЧ получаются изображения такого типа:
Вейвлеты
Но что если использовать для свёртки с сигналом некую произвольную характеристическую функцию? Тогда это будет называться «Вейвлет-преобразование». Это определение вейвлетов не является корректным, но традиционно сложилось, что во многих командах вейвлет-анализом называется поиск произвольного паттерна на изображении при помощи свёртки с моделью этого паттерна. Существует набор классических функций, используемых в вейвлет-анализе. К ним относятся вейвлет Хаара, вейвлет Морле, вейвлет мексиканская шляпа, и.т.д. Примитивы Хаара, про которые было несколько моих прошлых статей (1, 2), относятся к таким функциям для двумерного пространства.
Выше приведено 4 примера классических вейвлетов. 3х-мерный вейвлет Хаара, 2х-мерные вейвлет Мейера, вейвлет Мексиканская Шляпа, вейвлет Добеши. Хорошим примером использования расширеной трактовки вейвлетов является задачка поиска блика в глазу, для которой вейвлетом является сам блик:
Классические вейвлеты обычно используются для сжатия изображений, или для их классификации (будет описано ниже).
Корреляция
После такой вольной трактовки вейвлетов с моей стороны стоит упомянуть собственно корреляцию, лежащую в их основе. При фильтрации изображений это незаменимый инструмент. Классическое применение — корреляция видеопотока для нахождения сдвигов или оптических потоков. Простейший детектор сдвига — тоже в каком-то смысле разностный коррелятор. Там где изображения не коррелируют — было движение.
Фильтрации функций
Интересным классом фильтров является фильтрация функций. Это чисто математические фильтры, которые позволяют обнаружить простую математическую функцию на изображении (прямую, параболу, круг). Строится аккумулирующее изображение, в котором для каждой точки исходного изображения отрисовывается множество функций, её порождающих. Наиболее классическим преобразованием является преобразование Хафа для прямых. В этом преобразовании для каждой точки (x;y) отрисовывается множество точек (a;b) прямой y=ax+b, для которых верно равенство. Получаются красивые картинки:
(первый плюсег тому, кто первый найдёт подвох в картинке и таком определении и объяснит его, второй плюсег тому, кто первый скажет что тут изображено)
Преобразование Хафа позволяет находить любые параметризуемые функции. Например окружности. Есть модифицированное преобразование, которое позволяет искать любые фигуры. Это преобразование ужасно любят математики. Но вот при обработке изображений, оно, к сожалению, работает далеко не всегда. Очень медленная скорость работы, очень высокая чувствительность к качеству бинаризации. Даже в идеальных ситуациях я предпочитал обходиться другими методами.
Аналогом преобразования Хафа для прямых является преобразование Радона . Оно вычисляется через БПФ, что даёт выигрыш производительности в ситуации, когда точек очень много. К тому же его возможно применять к не бинаризованному изображению.
Фильтрации контуров
Отдельный класс фильтров — фильтрация границ и контуров . Контуры очень полезны, когда мы хотим перейти от работы с изображением к работе с объектами на этом изображении. Когда объект достаточно сложный, но хорошо выделяемый, то зачастую единственным способом работы с ним является выделение его контуров. Существует целый ряд алгоритмов, решающих задачу фильтрации контуров:
Чаще всего используется именно Кэнни, который хорошо работает и реализация которого есть в OpenCV (Собель там тоже есть, но он хуже ищёт контуры).
Прочие фильтры
Сверху приведены фильтры, модификации которых помогают решить 80-90% задач. Но кроме них есть более редкие фильтры, используемые в локальных задачах. Таких фильтров десятки, я не буду приводить их все. Интересными являются итерационные фильтры (например активная модель внешнего вида), а так же риджлет и курвлет преобразования, являющиеся сплавом классической вейвлет фильтрации и анализом в поле радон-преобразования. Бимлет-преобразование красиво работает на границе вейвлет преобразования и логического анализа, позволяя выделить контуры:
Но эти преобразования весьма специфичны и заточены под редкие задачи.
Часть 2. Логическая обработка результатов фильтрации
Фильтрация даёт набор пригодных для обработки данных. Но зачастую нельзя просто взять и использовать эти данные без их обработки. В этом разделе будет несколько классических методов, позволяющих перейти от изображения к свойствам объектов, или к самим объектам.
Морфология
Переходом от фильтрации к логике, на мой взгляд, являются методы математической морфологии (1, 2 , 3). По сути, это простейшие операции наращивания и эрозии бинарных изображений. Эти методы позволяют убрать шумы из бинарного изображения, увеличив или уменьшив имеющиеся элементы. На базе математической морфологии существуют алгоритмы оконтуривания, но обычно пользуются какими-то гибридными алгоритмами или алгоритмами в связке.
Контурный анализ
В разделе по фильтрации уже упоминались алгоритмы получения границ. Полученные границы достаточно просто преобразуются в контуры. Для алгоритма Кэнни это происходит автоматически, для остальных алгоритмов требуется дополнительная бинаризация. Получить контур для бинарного алгоритма можно например алгоритмом жука.
Контур является уникальной характеристикой объекта. Часто это позволяет идентифицировать объект по контуру. Существует мощный математический аппарат, позволяющий это сделать. Аппарат называется контурным анализом (1, 2 ).
Если честно, то у меня ни разу ни получилось применить контурный анализ в реальных задачах. Уж слишком идеальные условия требуются. То граница не найдётся, то шумов слишком много. Но, если нужно что-то распознавать в идеальных условиях — то контурный анализ замечательный вариант. Очень быстро работает, красивая математика и понятная логика.
Особые точки
Особые точки это уникальные характеристики объекта, которые позволяют сопоставлять объект сам с собой или с похожими классами объектов. Существует несколько десятков способов позволяющих выделить такие точки. Некоторые способы выделяют особые точки в соседних кадрах, некоторые через большой промежуток времени и при смене освещения, некоторые позволяют найти особые точки, которые остаются таковыми даже при поворотах объекта. Начнём с методов, позволяющих найти особые точки, которые не такие стабильные, зато быстро рассчитываются, а потом пойдём по возрастанию сложности:
Первый класс. Особые точки, являющиеся стабильными на протяжении секунд. Такие точки служат для того, чтобы вести объект между соседними кадрами видео, или для сведения изображения с соседних камер. К таким точкам можно отнести локальные максимумы изображения, углы на изображении (лучший из детекторов, пожалуй, детектор Хариса), точки в которых достигается максимумы дисперсии, определённые градиенты и.т.д.
Второй класс. Особые точки, являющиеся стабильными при смене освещения и небольших движениях объекта. Такие точки служат в первую очередь для обучения и последующей классификации типов объектов. Например, классификатор пешехода или классификатор лица — это продукт системы, построенной именно на таких точках. Некоторые из ранее упомянутых вейвлетов могут являются базой для таких точек. Например, примитивы Хаара, поиск бликов, поиск прочих специфических функций. К таким точкам относятся точки, найденные методом гистограмм направленных градиентов (HOG).
Третий класс. Стабильные точки. Мне известно лишь про два метода, которые дают полную стабильность и про их модификации. Это SURF и SIFT. Они позволяют находить особые точки даже при повороте изображения. Расчёт таких точек осуществляется дольше по сравнению с остальными методами, но достаточно ограниченное время. К сожалению эти методы запатентованы. Хотя, в России патентовать алгоритмы низя, так что для внутреннего рынка пользуйтесь.
Часть 3. Обучение
ретья часть рассказа будет посвящена методам, которые не работают непосредственно с изображением, но которые позволяют принимать решения. В основном это различные методы машинного обучения и принятия решений. Недавно Яндыкс выложил на Хабр курс по этой тематике, там очень хорошая подборка. Вот тут оно есть в текстовой версии. Для серьёзного занятия тематикой настоятельно рекомендую посмотреть именно их. Тут я попробую обозначить несколько основных методов используемых именно в распознавании образов.
В 80% ситуаций суть обучения в задаче распознавания в следующем:
Имеется тестовая выборка, на которой есть несколько классов объектов. Пусть это будет наличие/отсутствие человека на фотографии. Для каждого изображения есть набор признаков, которые были выделены каким-нибудь признаком, будь то Хаар, HOG, SURF или какой-нибудь вейвлет. Алгоритм обучения должен построить такую модель, по которой он сумеет проанализировать новое изображение и принять решение, какой из объектов имеется на изображении.
Как это делается? Каждое из тестовых изображений — это точка в пространстве признаков. Её координаты это вес каждого из признаков на изображении. Пусть нашими признаками будут: «Наличие глаз», «Наличие носа», «Наличие двух рук», «Наличие ушей», и.т.д… Все эти признаки мы выделим существующими у нас детекторами, которые обучены на части тела, похожие на людские. Для человека в таком пространстве будет корректной точка [1;1;1;1;..]. Для обезьяны точка [1;0;1;0…] для лошади [1;0;0;0…]. Классификатор обучается по выборке примеров. Но не на всех фотографиях выделились руки, на других нет глаз, а на третьей у обезьяны из-за ошибки классификатора появился человеческий нос. Обучаемый классификатор человека автоматически разбивает пространство признаков таким образом, чтобы сказать: если первый признак лежит в диапазоне 0.5
По существу цель классификатора — отрисовать в пространстве признаков области, характеристические для объектов классификации. Вот так будет выглядеть последовательное приближение к ответу для одного из классификаторов (AdaBoost) в двумерном пространстве:
Существует очень много классификаторов. Каждый из них лучше работает в какой-то своей задачке. Задача подбора классификатора к конкретной задаче это во многом искусство. Вот тут немножко красивых картинок на тему.
Простой случай, одномерное разделение
Разберём на примере самый простой случай классификации, когда пространство признака одномерное, а нам нужно разделить 2 класса. Ситуация встречается чаще, чем может представиться: например, когда нужно отличить два сигнала, или сравнить паттерн с образцом. Пусть у нас есть обучающая выборка. При этом получается изображение, где по оси X будет мера похожести, а по оси Y -количество событий с такой мерой. Когда искомый объект похож на себя — получается левая гауссиана. Когда не похож — правая. Значение X=0.4 разделяет выборки так, что ошибочное решение минимизирует вероятность принятия любого неправильного решения. Именно поиском такого разделителя и является задача классификации.
Маленькая ремарка. Далеко не всегда оптимальным будет тот критерий, который минимизирует ошибку. Следующий график — это график реальной системы распознавания по радужной оболочке. Для такой системы критерий выбирается такой, чтобы минимизировать вероятность ложного пропуска постороннего человека на объект. Такая вероятность называется «ошибка первого рода», «вероятность ложной тревоги», «ложное срабатывание». В англоязычной литературе «False Access Rate ».
Что делать если измерений больше двух?
Алгоритмов много. Даже очень много. Если хотите подробно узнать про каждый из них читайте курс Воронцова, ссылка на который дана выше, и смотрите лекции Яндыкса. Сказать, какой из алгоритмов лучше для какой задачи часто заранее невозможно. Тут я попробую выделить основные, которые в 90% помогут новичку с первой задачей и реализацию которых на вашем языке программирования вы достоверно найдёте в интернете.
k-means (1, 2, 3 ) — один из самых простых алгоритмов обучения. Конечно, он в основном для кластеризации, но и обучить через него тоже можно. Работает в ситуации, когда группы объектов имеют неплохо разнесённый центр масс и не имеют большого пересечения.
AdaBoost (1, 2, 3) АдаБуста — один из самых распространённых классификаторов. Например каскад Хаара построен именно на нём. Обычно используют когда нужна бинарная классификация, но ничего не мешает обучить на большее количество классов.
SVM (1, 2, 3, 4 ) Один из самых мощных классификаторов, имеющий множество реализаций. В принципе, на задачах обучения, с которыми я сталкивался, он работал аналогично адабусте. Считается достаточно быстрым, но его обучение сложнее, чем у Адабусты и требуется выбор правильного ядра.
Ещё есть нейронные сети и регрессия. Но чтобы кратко их классифицировать и показать, чем они отличаются, нужна статья куда больше, чем эта.
________________________________________________
Надеюсь, у меня получилось сделать беглый обзор используемых методов без погружения в математику и описание. Может, кому-то это поможет. Хотя, конечно, статья неполна и нет ни слова ни о работе со стереоизображениями, ни о МНК с фильтром Калмана, ни об адаптивном байесовом подходе.
Если статья понравится, то попробую сделать вторую часть с подборкой примеров того, как решаются существующие задачки ImageRecognition.
И напоследок
Что почитать?
1) Когда-то мне очень понравилась книга «Цифровая обработка изображений» Б. Яне, которая написана просто и понятно, но в то же время приведена почти вся математика. Хороша для того, чтобы ознакомиться с существующими методами.
2) Классикой жанра является Р Гонсалес, Р. Вудс » Цифровая обработка изображений «. Почему-то она мне далась сложнее, чем первая. Сильно меньше математики, зато больше методов и картинок.
3) «Обработка и анализ изображений в задачах машинного зрения» — написана на базе курса, читаемого на одной из кафедр ФизТеха. Очень много методов и их подробного описания. Но на мой взгляд в книге есть два больших минуса: книга сильно ориентирована на пакет софта, который к ней прилагается, в книге слишком часто описание простого метода превращается в математические дебри, из которых сложно вынести структурную схему метода. Зато авторы сделали удобный сайт, где представлено почти всё содержание — wiki.technicalvision.ru
4) Почему-то мне кажется, что хорошая книжка, которая структурирует и увязывает картину мира, возникающую при занятии Image Recognition и Machine Learning — это «Об интеллекте» Джеффа Хокинса. Прямых методов там нет, но есть много мыслей на подумать, откуда прямые методы обработки изображений происходят. Когда вчитываешься, понимаешь, что методы работы человеческого мозга ты уже видел, но в задачах обработки видео.
Исследование методов сегментации изображений / Хабр
В статье описано исследование методов сегментации изображений на различных примерах. Целью исследования является обнаружение достоинств и недостатков некоторых известных методов.
Методы, которые будут рассмотрены в данной статье:
- Метод выращивания регионов Тут можно почитать про метод выращивания регионов;
- Метод водораздела А тут подробно про метод водораздела, еще и с кодом;
- Метод нормальных разрезов Подробнее почитать можно тут.
Исследование методов сегментации на модельных изображениях
Исследование методов сегментации первоначально проводилось моделях изображений. В качестве моделей использовались девять видов изображений.
| Название метода | Результаты |
|---|---|
| Метод выращивания регионов | |
| Метод водораздела | |
| Метод нормальных разрезов |
Результаты исследования показали:
- Метод выращивания регионов локализует дефекты текстуры как резко отличающиеся от фона, так и образованные поворотом и изменением яркости текстуры;
- Метод выращивания регионов в различной степени локализует дефекты при разных углах поворота текстуры;
- Рассмотренный метод сегментации водораздела в исходном виде не обеспечивает локализацию текстурных дефектов;
- Метод нормальных разрезов хорошо локализует наличие текстуры отличной от фона, но не выделяет изменение яркости и поворот текстуры.
Исследование методов сегментации на изображениях объекта
Для исследования методов сегментации было подготовлена база изображений различных объектов. Полученные изображения прошли сегментацию с помощью различных методов, результат которой представлен на рисунках в таблице
Результаты:
- Метод выращивания регионов не обеспечивает локализацию сегментов на изображениях объекта;
- Рассмотренные методы водораздела и нормальных разрезов в исходном виде не обеспечивают локализацию представленных объектов;
- Метод нормальных разрезов обеспечивает локализацию объектов на изображениях объектов.
Результаты
Результаты проведенного исследования:
- Метод выращивания регионов не обеспечивает локализацию сегментов как на модельных изображениях, так и на изображениях объекта, а также обеспечивает локализацию элементов дорожно-транспортной инфраструктуры.
- Рассмотренные методы водораздела и нормальных разрезов в исходном виде не полностью обеспечивают локализацию представленных объектов.
- Метод нормальных разрезов обеспечивает локализацию объектов как на модельных изображениях, так и на изображениях объектов, а также обеспечивает локализацию элементов дорожно-транспортной инфраструктуры.
- Метод выращивания регионов и метод нормальных разрезов могут быть рекомендованы для использования в автоматизированных системах визуального контроля.
Microsoft Office PowerPoint 2003 Visual Basic Справочник
документация .HELP! Документация по Microsoft PowerPoint Visual Basic
Microsoft PowerPoint Visual Basic
Содержание
- Справочник по Microsoft PowerPoint Visual Basic
- Объектная модель Microsoft PowerPoint
- Что нового
- Новые объекты
- Новые свойства (алфавитный список)
- Новые свойства (по объектам)
- Новые методы (по объектам)
- Новые события
- Концепции программирования
- Работа с презентациями
- Использование событий с объектом приложения
- Работа с фигурами (объектами рисования)
- Работа с панелями и представлениями
- Публикация веб-презентации
- Работа с элементами управления и диалоговыми окнами
- Использование элементов управления ActiveX на слайдах
- Использование элементов управления ActiveX в документе
- Создание настраиваемого диалогового окна
- Работа с другими приложениями
- Управление одним приложением Microsoft Office из другого
- Программные идентификаторы OLE
- Работа с презентациями
- Коллекции
- Коллекция ActionSettings
- Коллекция AddIns
- Коллекция корректировок
- Коллекция AnimationBehaviors
- Коллекция AnimationPoints
- В
- Коллекция границ
- С
- Коллекция CellRange
- Коллекция ColorSchemes
- Коллекция столбцов
- Сборник комментариев
- D
- Коллекция дизайнов
- Коллекция DiagramNodes
- DocumentWindows Коллекция
- F
- Коллекция шрифтов
- ЧАС
- Коллекция HeadersFooters
- Коллекция гиперссылок
- N
- Коллекция NamedSlideShows
- п
- Коллекция панелей
- Коллекция заполнителей
- Коллекция презентаций
- Коллекция PrintRanges
- Коллекция PublishObjects
- р
- Коллекция строк
- Коллекция RulerLevels
- S
- Коллекция последовательностей
- Коллекция последовательностей
- Коллекция ShapeNodes
- Коллекция фигур
- Коллекция SlideRange
- Коллекция слайдов
- SlideShowWindows Коллекция
- T
- Коллекция TabStops
- Коллекция TextStyleLevels
- Коллекция текстовых стилей
- Объекты
- Объект ActionSetting
- Добавить объект
- Объект AnimationBehavior
- Объект AnimationPoint
- Объект AnimationSettings
- Объект приложения
- Автозамена объекта
- В
- Объект BulletFormat
- С
- CalloutFormat Object
- Объект ячейки
- Объект ColorEffect
- ColorFormat Объект
- Объект ColorScheme
- Столбец Объект
- Объект CommandEffect
- Объект комментария
- ConnectorFormat Объект
- D
- Объект DefaultWebOptions
- Объект дизайна
- Объект диаграммы
- Объект DiagramNode
- Объект DiagramNodeChildren
- Объект DocumentWindow
- Е
- Объект эффекта
- Объект EffectInformation
- Объект EffectParameters
- Объект ExtraColors
- F
- Объект FillFormat
- Объект FilterEffect
- Объект шрифта
- Объект FreeformBuilder
- грамм
- Объект GroupShapes
- ЧАС
- Объект HeaderFooter
- Объект гиперссылки
- L
- Объект LineFormat
- LinkFormat Object
- M
- Мастер-объект
- Объект MotionEffect
- N
- Объект NamedSlideShow
- О
- Объект ObjectVerbs
- Объект OLEFormat
- Объект параметров
- п
- Объект PageSetup
- Панель объекта
- Объект ParagraphFormat
- Объект PictureFormat
- Объект PlaceholderFormat
- Объект PlaySettings
- Объект презентации
- Объект PrintOptions
- Объект PrintRange
- Объект PropertyEffect
- Объект PublishObject
- р
- RGBColor объект
- Объект RotationEffect
- Строка объекта
- Линейка Объект
- Объект RulerLevel
- S
- Объект ScaleEffect
- Объект выбора
- SetEffect объект
- Объект ShadowFormat
- Объект формы
- Объект ShapeNode
- Объект ShapeRange
- Сдвинуть объект
- Объект SlideShowSettings
- Объект SlideShowTransition
- Объект SlideShowView
- Объект SlideShowWindow
- Объект SoundEffect
- T
- Объект таблицы
- TabStop объект
- Теги Объект
- Объект TextEffectFormat
- Объект TextFrame
- Объект TextRange
- TextStyle Object
- Объект TextStyleLevel
- Объект ThreeDFormat
- Объект TimeLine
- Объект синхронизации
- В
- Просмотр объекта
- W
- Объект WebOptions
- методы
- Активировать метод
- Добавить метод
- AddBaseline Метод
- AddCallout метод
- AddComment метод
- AddConnector Метод
- AddCurve Метод
- Метод AddDiagram
- AddEffect Метод
- AddLabel Метод
- AddLine метод
- AddMediaObject Метод
- AddNode Метод
- AddNodes Метод
- AddOLEObject Метод
- AddPeriods Метод
- AddPicture Метод
- AddPlaceholder метод
- AddPolyline метод
- AddShape Метод
- AddTable метод
- AddTextbox Метод
- AddTextEffect Метод
- AddTitle Метод
- AddTitleMaster Метод
- AddToFavorites Метод
- Метод выравнивания
- Применить метод
- ApplyTemplate Метод
- Способ размещения
- Автоматический метод длины
- В
- Фоновый метод
- BeginConnect Метод
- Метод BeginDisconnect
- Метод BuildFreeform
- С
- Метод CanCheckIn
- Метод CanCheckOut
- Ячейка Метод
- Метод ChangeCase
- Метод символов
- Метод регистрации
- Метод CheckOut
- Очистить метод
- Метод ClearAll
- Клонировать метод
- CloneNode Метод
- Метод закрытия
- Цвета Метод
- Преобразовать метод
- ConvertToAfterEffect Метод
- ConvertToAnimateBackground — метод
- ConvertToAnimateInReverse — метод
- ConvertToBuildLevel метод
- ConvertToShape Метод
- ConvertToTextUnitEffect — метод
- Метод копирования
- CreateNewDocument Метод
- CustomDrop метод
- CustomLength метод
- Метод резки
- D
- Удалить метод
- DeleteText Метод
- Метод распределения
- Метод Доверба
- Метод DrawLine
- Повторяющийся метод
- Е
- EndConnect Метод
- Метод EndDisconnect
- EndNamedShow Метод
- Метод EndReview
- EraseDrawing Method
- Метод выхода
- Метод экспорта
- F
- Найти метод
- Метод FindBySlideID
- FindFirstAnimationFor Метод
- FindFirstAnimationForClick Метод
- Первый метод
- FitToPage Метод
- Метод переворота
- Следуйте методу
- FollowHyperlink метод
- грамм
- GotoNamedShow Метод
- GotoSlide метод
- Групповой метод
- ЧАС
- Метод помощи
- я
- ImportFromFile Метод
- Метод увеличения яркости
- Метод увеличения контрастности
- Метод IncrementLeft
- Метод IncrementOffsetX
- Метод IncrementOffsetY
- Метод IncrementRotation
- Метод IncrementRotationX
- Метод IncrementRotationY
- Метод IncrementTop
- Вставить метод
- InsertAfter метод
- InsertBefore метод
- InsertDateTime метод
- InsertFromFile Метод
- InsertSlideNumber — метод
.
Метод сравнения | Документация TestComplete
Относится к TestComplete 14.60, последнее изменение 18 августа 2020 г.
Описание
Метод Picture.Compare сравнивает два изображения попиксельно (первое изображение представлено заданным объектом Picture , второе определяется параметром Picture) и возвращает True, если изображения идентичны, или False в противном случае.
Чтобы узнать больше о сравнении изображений, прочтите тему «Как работает сравнение изображений».
Декларация
PictureObj . Сравните ( Picture , Transparent , PixelTolerance , Mouse , ColorTolerance , Mask )
| PictureObj | Выражение, переменная или параметр, указывающий ссылку на объект изображения | |||
| Изображение | [дюйм] | Требуется | A Picture объект или объект, который имеет метод Picture , который возвращает объект Picture | |
| Прозрачный | [дюйм] | Дополнительно | логический | Значение по умолчанию: Ложь |
| PixelTolerance | [дюйм] | Дополнительно | Целое число | Значение по умолчанию: 0 |
| Мышь | [дюйм] | Дополнительно | логический | Значение по умолчанию: Правда |
| Допуск цвета | [дюйм] | Дополнительно | Целое число | Значение по умолчанию: 0 |
| Маска | [дюйм] | Дополнительно | A Изображение объект | Значение по умолчанию: Пустая строка |
| Результат | логический | |||
Применимо к
Метод применен к следующему объекту:
Параметры
Метод имеет следующие параметры:
Изображение
Объект Picture , представляющий изображение для сравнения с изображением PictureObj.В качестве альтернативы, это может быть объект, у которого есть метод Picture , который возвращает желаемый объект Picture .
прозрачный
По умолчанию — ложь. Если это True, то верхний левый пиксель данного изображения будет рассматриваться как «прозрачный» (фоновый) цвет в этом изображении.
Таким образом, любые прозрачные пиксели в первом изображении будут исключены, когда
сравнивается со вторым изображением.
Допуск пикселей
Позволяет игнорировать небольшие различия между растровыми изображениями во время поиска.Если количество разных пикселей меньше или равно PixelTolerance, TestComplete считает изображения идентичными. 0 — значение по умолчанию; это означает, что никакие различия между растровыми изображениями, кроме тех, которые заданы параметром Transparent, не игнорируются.
| Примечание: | Использование параметра PixelTolerance с ненулевыми значениями может замедлить процесс поиска. |
Мышь
Этот параметр имеет значение, только если —
— и —
Если параметр Mouse имеет значение True, метод Compare включает указатель мыши в изображение Picture.Метод вернет True только в том случае, если Picture также содержит изображение указателя мыши в той же позиции.
Допуск цвета
Позволяет игнорировать различия оттенков при сравнении растровых изображений. Параметр указывает допустимую разницу в цвете, при которой два пикселя определенного цвета следует рассматривать как идентичные. Разница в цвете представлена в виде целого числа в диапазоне 0… 255, которое указывает допустимую разницу для каждого цветового компонента (красного, зеленого и синего) сравниваемых пикселей.Два пикселя считаются идентичными, если разница между интенсивностями каждой из их цветовых составляющих не превышает заданного значения.
Когда ColorTolerance равен 0, что является значением по умолчанию, сравниваемые пиксели считаются идентичными, только если они имеют точно такой же цвет . Когда ColorTolerance равно 255, пиксели любого цвета считаются идентичными.
Маска
Указывает, какие области растровых изображений следует сравнивать.Маска — это еще один объект Picture , пиксели которого могут быть как черными, так и белыми. Если указана маска, процедура работает следующим образом: белые пиксели маски учитываются при сравнении, а черные пиксели игнорируются.
Результат
Истина, если сравниваемые изображения идентичны, и Ложь в противном случае.
Замечания
Если сравнение не удается, а изображения кажутся идентичными, прочтите разделы справки «Почему не удается сравнить изображения» и «Факторы, влияющие на сравнение изображений», чтобы определить причину сбоя.
Пример
Следующий код сравнивает два изображения, которые представлены объектами Picture .
См. Также
О контрольных точках региона
Как работает сравнение изображений
Метод сравнения
Метод проверки
Метод поиска
Метод различия
Свойство пикселей
,
Метод различия | Документация TestComplete
Относится к TestComplete 14.60, последнее изменение 18 августа 2020 г.
Описание
Метод Picture.Difference сравнивает два изображения попиксельно (первое изображение представлено заданным объектом Picture , второе определяется параметром Picture) и возвращает изображение, показывающее различия между сравниваемыми растровыми изображениями.Это результирующее изображение также представлено объектом Picture .
Чтобы узнать больше о сравнении изображений, прочтите тему «Как работает сравнение изображений».
Декларация
PictureObj .Difference ( Picture , Transparent , PixelTolerance , Mouse , ColorTolerance , Mask )
| Изображение Obj | Выражение, переменная или параметр, указывающий ссылку на объект изображения | |||
| Изображение | [дюйм] | Требуется | A Picture объект или объект, который имеет метод Picture , который возвращает объект Picture | |
| прозрачный | [дюйм] | Дополнительно | логическое значение | Значение по умолчанию: Ложь |
| PixelTolerance | [дюйм] | Дополнительно | Целое число | Значение по умолчанию: 0 |
| Мышь | [дюйм] | Дополнительно | логическое значение | Значение по умолчанию: Правда |
| Допуск цвета | [дюйм] | Дополнительно | Целое число | Значение по умолчанию: 0 |
| Маска | [дюйм] | Дополнительно | A Изображение объект | |
| Результат | A Изображение объект | |||
Применимо к
Метод применен к следующему объекту:
Параметры
Метод имеет следующие параметры:
Изображение
Объект Picture , представляющий изображение, которое нужно сравнить с данным изображением.В качестве альтернативы, это может быть объект, у которого есть метод Picture , который возвращает желаемый объект Picture .
Прозрачный
По умолчанию — ложь. Если это True, верхний левый пиксель данного изображения будет рассматриваться как «прозрачный» (фоновый) цвет в этом изображении. Поэтому любые прозрачные пиксели в первом изображении будут исключены по сравнению со вторым изображением. Все пиксели этого цвета исключаются из сравнения.
Допуск пикселей
Позволяет игнорировать небольшие различия между растровыми изображениями во время поиска.Если количество разных пикселей меньше или равно PixelTolerance, TestComplete считает изображения идентичными. 0 — значение по умолчанию; это означает, что никакие различия между растровыми изображениями, кроме тех, которые заданы параметром Transparent, не игнорируются.
| Примечание: | Использование параметра PixelTolerance с ненулевыми значениями может замедлить процесс поиска. |
Мышь
Этот параметр имеет значение, только если —
— и —
Если параметр Mouse имеет значение True, метод Find включает указатель мыши в изображение Picture.
Цвет Допуск
Позволяет игнорировать различия оттенков при сравнении растровых изображений. Параметр указывает допустимую разницу в цвете, при которой два пикселя определенного цвета следует рассматривать как идентичные. Разница в цвете представлена в виде целого числа в диапазоне 0… 255, которое указывает допустимую разницу для каждого цветового компонента (красного, зеленого и синего) сравниваемых пикселей. Два пикселя считаются идентичными, если разница между интенсивностями каждой из их цветовых составляющих не превышает заданного значения.
Когда ColorTolerance имеет значение 0, которое является значением по умолчанию, сравниваемые пиксели считаются идентичными, только если они имеют точно такой же цвет и . Когда ColorTolerance равен 255, пиксели любого цвета считаются идентичными.
Маска
Указывает, какие области растровых изображений следует сравнивать. Маска — это еще один объект Picture , пиксели которого могут быть как черными, так и белыми. Если указана маска, процедура работает следующим образом: белые пиксели маски учитываются при сравнении, а черные пиксели игнорируются.
Результат
Если сравниваемые изображения идентичны, метод Difference возвращает пустое значение ( Nothing в VBScript, null в JavaScript, JScript, C ++ Script и C # Script, None в Python и nil в DelphiScript). Если изображения различаются, метод возвращает изображение (представленное объектом Picture ), которое показывает разницу между изображениями. Используется следующая схема цветового выделения:
- Одинаковые пиксели залиты белым цветом.
- Пиксели, которые отличаются от одного изображения к другому, выделяются красным цветом.
- Лишние участки (при разной высоте или ширине изображений) выделяются фуксией.
- Несходные пиксели, пропущенные из-за параметра PixelTolerance, выделяются синим цветом.
- Пиксели, пропущенные из-за параметра «Прозрачный» или «Маска», залиты серым цветом.
- Пиксели, которые были проигнорированы из-за параметра ColorTolerance, выделены желтым цветом.
Примечания
Чтобы узнать, почему метод сообщает, что изображения разные, хотя они кажутся идентичными (и, наоборот, почему метод сообщает, что изображения идентичны, хотя они разные), см. «Факторы, влияющие на сравнение изображений» и «Почему не удается сравнить изображения».
Пример
Следующий код сравнивает два изображения, которые представлены объектами Picture .
См. Также
О контрольных точках региона
Как работает сравнение изображений
Факторы, влияющие на сравнение изображений
Почему не удается сравнить изображения
Метод сравнения
Метод сравнения
Метод поиска
Свойство пикселей
,
iphone — способ сделать снимок на камеру OverlayView
Переполнение стека
- Около
Товары
- Для команд
Переполнение стека
Общественные вопросы и ответыПереполнение стека для команд
Где разработчики и технологи делятся частными знаниями с коллегамиработы
Программирование и связанные с ним технические возможности карьерного ростаТалант
Нанимайте технических специалистов и создавайте свой бренд работодателяреклама
Обратитесь к разработчикам и технологам со всего мира- О компании
,
