Проектирование векторов на оси | LAMPA
Проектирование вектора на ось, когда задан угол между вектором и осью
Очень часто (а вернее — почти всегда) бывает так, что задан угол между вектором и осью, а также длина вектора, а на оси нет никаких обозначений координат. Тогда проекцию вектора ищут с помощью косинуса или синуса. Рассмотрим все на конкретном примере.
Пусть у нас есть вектор a⃗\vec{a}a⃗.
Из его начала проведем нужные нам оси XXX и YYY, на которые будем проектировать наш вектор.
Из конца вектора опускаем перпендикуляры на оси XXX и YYY.
Получается прямоугольник. Стороны этого прямоугольника и есть проекции вектора a⃗\vec{a}a⃗: axa_{x}ax и aya_{y}ay.
Видно, что у нас получился прямоугольный треугольник.
Его стороны как раз проекции нашего вектора. Наверняка вы помните (а тем, кто не помнит, я напоминаю), что в прямоугольном треугольнике
Наверняка вы помните (а тем, кто не помнит, я напоминаю), что в прямоугольном треугольнике
cosα=прилежащий катетгипотенуза\cos \alpha=\frac{\text{прилежащий катет}}{\text{гипотенуза}}cosα=гипотенузаприлежащий катет
sinα=противолежащий катетгипотенуза\sin \alpha=\frac{\text{противолежащий катет}}{\text{гипотенуза}}sinα=гипотенузапротиволежащий катет.
В нашем треугольнике то же самое:
cosα=axa\cos \alpha=\frac{a_{x}}{a}cosα=aax
sinα=aya\sin \alpha = \frac{a_{y}}{a}sinα=aay.
Или:
ax=a⋅cosαa_{x}=a\cdot \cos \alphaax=a⋅cosα;
ay=a⋅sinαa_{y}=a\cdot \sin \alphaay=a⋅sinα.
Итак:
Проекция на прилежащую ось — это умножение на косинус.
Проекция на противолежащую ось — это умножение на синус.
Вектор, действия с векторами, сложение и вычитание
Тестирование онлайн
Проекция вектора
Сложение и вычитание векторов
Вектор
Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону
Вектор -c — это вектор c, но противоположного направления. Тогда
Проекция вектора
Проекция вектора на ось имеет положительное значение в том случае, когда направление вектора совпадает с направлением оси. Отрицательное значение — в противоположном случае.
Отрицательное значение — в противоположном случае.
Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: sx=x-x0, на ось ОУ: sy=y-y0.
Рассмотрим примеры
Частные случаи, когда проекция на ось Ox или Oy нулевая.
Сумма составляющих вектора по осям равна данному вектору, т.е.
Сложение векторов
Правило параллелограмма: диагональ параллелограмма — сумма двух векторов с общим началом.
Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.
Рассмотрим правила на примерах.
Вычитание векторов
Вычитание векторов — это сумма положительного и отрицательного вектора.
Упражнения
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?
Проекция вектора на координатную ось.

Проекцией вектора
на ось называется вектор, который получается в результате перемножения
скалярной проекции вектора на эту ось и единичного вектора этой оси.
Например, если аx – скалярная проекция вектора а на ось X, то аx·i — его векторная проекция на эту ось.
Обозначим векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим аx (жирная буква, обозначающая вектор и нижний индекс названия оси) или (нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).
Скалярной проекцией вектора на ось называется число,
абсолютная величина которого равна длине отрезка оси (в выбранном
масштабе), заключённого между проекциями точки начала и точки конца
вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция.
Проекция обозначается той же буквой, что и проектируемый вектор (в
обычном, нежирном написании), с нижним (как правило) индексом названия
оси, на которую этот вектор проектируется. Например, если на ось Х
проектируется вектора, то его проекция обозначается аx. При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться аy .
Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
аx = хк − xн.
Проекция вектора на ось — это число. Причем, проекция может быть положительной, если величина хк больше величины хн,
отрицательной, если величина хк меньше величины хн
и равной нулю, если хк равно хн .
Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Из рисунка видно, что аx = а Cos α
то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то
Cos α > 0 и аx > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.
Углы,
отсчитываемые от оси против хода часовой стрелки, принято считать
положительными, а по ходу — отрицательными. Однако, поскольку косинус –
функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций
углы можно отсчитывать как по ходу часовой стрелки, так и против.
Чтобы
найти проекцию вектора на ось надо модуль этого вектора умножить на
косинус угла между направлением оси и направлением вектора.
Материалы взяты с: http://en.coolreferat.com
Проекции вектора на ось и на плоскость в теоретической механике
Проекции вектора на ось и на плоскость
Аналитический способ решения задач статики основан на применении метода проекции, знакомого студентам из векторной алгебры. Ввиду особой важности этого метода для дальнейшего, напомним его основы.
Ввиду особой важности этого метода для дальнейшего, напомним его основы.
Проекцией вектора на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка оси проекций, заключенного между проекциями на нее начала и конца данного вектора (рис. 24).
Проекция считается положительной, если переход от ее начала к концу совпадает с заданным положительным
направлением оси, и отрицательной — если с противоположным.
Проекцию вектора на ось принято обозначать теми же буквами, что и вектор, но обычного шрифта, указывая нижним индексом ось проекций.
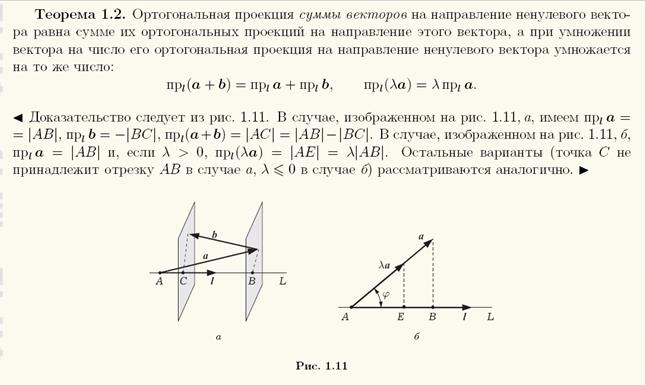
Проекции вектора на две параллельные и одинаково направленные оси равны между собой. Этим особенно удобно бывает пользоваться в тех случаях, когда вектор не лежит в одной плоскости с осью (рис. 24,(5). Из рис. 24, а и б имеем:
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между направлением вектора и положительным направлением оси проекций
Проекция будет положительной, если направление вектора составляет с положительным направлением оси острый угол, н отрицательной — если тупой.
Проекцией вектора на плоскость называется вектор, заключенный между проекциями на эту плоскость начала и конца данного вектора.
Так, например, проекцией_вектора
на плоскость (рис. 25) будет вектор .
По модулю проекция вектора на плоскость:
где
— угол между направлением вектора и направлением его проекции на плоскость.
Для нахождения проекции вектора на ось, не лежащую с ним в одной плоскости, иногда бывает удобно
спроектировать сначала вектор на плоскость, в которой лежит эта ось, а затем уже проекцию вектора на плоскость спроектировать на данную ось.
Так, проекция вектора
на ось (рис. 25):
где
— угол между направлениями вектора и оси .
Зная проекции вектора па оси прямоугольной декартовой системы координат, легко найти и модуль и направление вектора.
Так как модуль вектора равен диагонали прямоугольного параллелепипеда (рис. 26), ребра которого равны абсолютным значениям проекций вектора на оси координат, то модуль вектора
Модуль вектора равен квадратному корню из суммы квадратов его проекций на три любые взаимно перпендикулярные оси.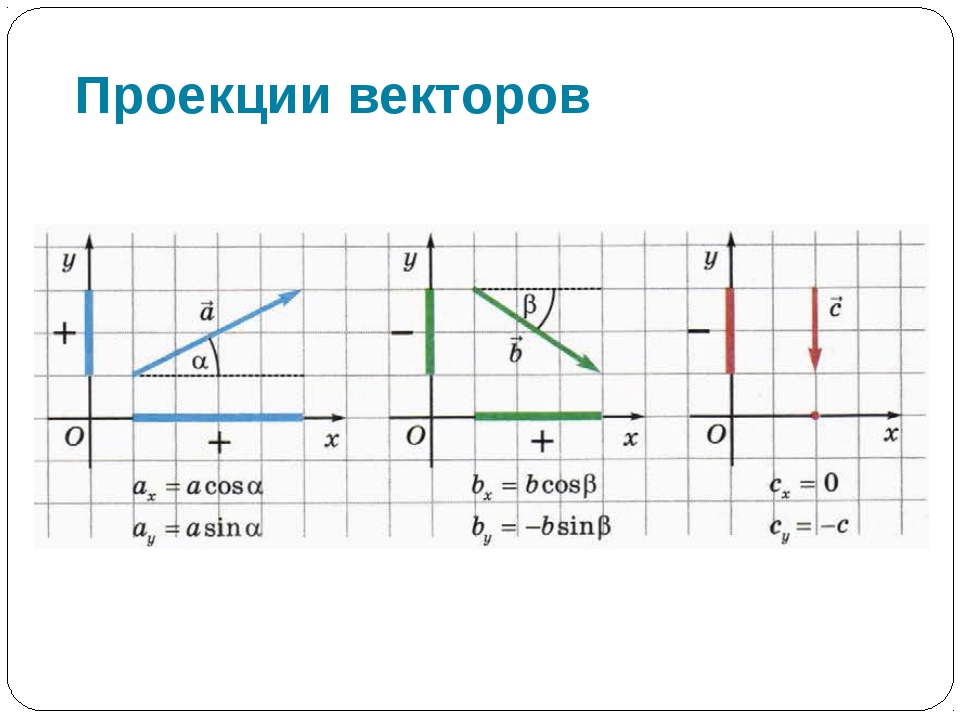
Направление вектора определяется из равенств:
Косинус угла между вектором и положительным направлением оси проекции называется направляющим косинусом. Он равен отношению проекции вектора на соответствующую ось к модулю вектора.
Заметим, что в формуле (4) надо брать арифметическое значение корня.
Вектор
(рис. 27) является замыкающем стороной векторного многоугольника , следовательно его можно рассматривать как геометрическую сумму составляющих векторов, расположенных па координатных осях
Век горы
и называются составляющими вектора но осям координат (или его компонентами).
Векторы
и совпадающие с положительными направлениями координатных осей и равные по модулю единице, называются единичными координатными векторами или координатными ортами соответствующих осей.
Составляющая вектора по оси координат равна проекции вектора на данную ось, умноженной на соответствующий координатный орт:
Подставляя последние выражения в предыдущее равенство. получаем весьма важную формулу разложения вектора по осям координат
получаем весьма важную формулу разложения вектора по осям координат
где коэффициенты
и при координатных ортах представляют собой проекции данного вектора на соответствующие координатные оси.
Пример задачи:
Даны проекции силы на оси прямоугольной системы координат
Написать формулу разложения заданной силы по осям координат, а также найти ее модуль и направление.
Решение:
По формуле
находим
Модуль силы
Направляющие косинусы
Отсюда, углы между направлением силы и положительными направлениями осей координат:
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
Проекция силы на ось
Решение
задач на равновесие сходящихся сил с
помощью построения замкнутых силовых
многоугольников в большинстве случаев
сопряжено с громоздкими построениями.
Более общим и универсальным методом
решения таких задач является переход
к определению проекций заданных сил на
координатные оси и оперирование с этими
проекциями. Осью
называют прямую линию, которой приписано
определенное направление. Проекция
вектора на ось является скалярной
величиной, которая определяется отрезком
оси, отсекаемым перпендикулярами,
опущенными на нее из начала и конца
вектора.
Проекция вектора считается положительной
(+), если направление от начала проекции
к ее концу совпадает с положительным
направлением оси.
Проекция
вектора считается отрицательной (—),
если направление от начала проекции к
ее концу противоположно положительному
направлению оси.Рассмотрим ряд случаев
проецирования сил на ось:
Вектор силы F (рис.12,a) составляет с
положительным направлением оси х острый
угол а. Чтобы найти проекцию, из начала
и конца вектора силы опускаем перпендикуляры
на ось х; получаем: .
Проекция вектора в данном случае
положительна.
Сила F (рис.12,б) составляет с положительным
направлением оси х тупой угол а.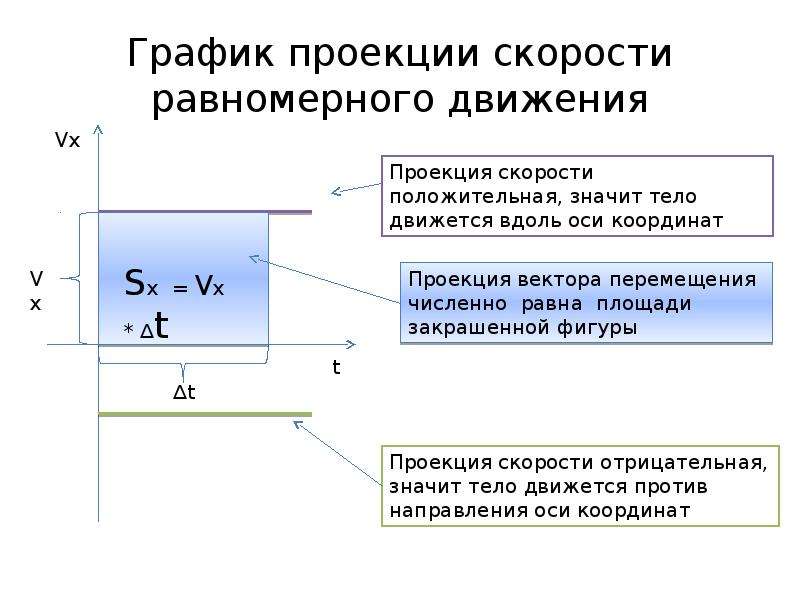 Тогда, т.
Тогда, т.
е. Fx = — F*cos р. Проекция силы F на ось х в
данном случае отрицательна
Сила F (рис.12,в) перпендикулярна оси х.
Проекция силы F на ось х равна нулю, т.е.
Fx — F cos 90° = 0.Итак, проекция силы на ось
координат равна произведению модуля
силы на косинус угла между вектором
силы и положительным направлением
оси.Силу, расположенную на плоскости
хОу (рис.13), можно спроектировать на две
координатные оси Ох и Оу. На рисунке
изображена сила F и ее проекции Fx, Fу.
Ввиду того, что проекции образуют между
собой прямой угол, из прямоугольного
треугольника АСВ следует: .
Этими формулами можно пользоваться для
определения модуля и направления силы,
когда известны ее проекции на координатные
оси.
Аналитический
способ нахождения равнодействующей
Геометрический способ нахождения
равнодействующей системы сил сопряжен
с определенными трудностями, особенно
в случае большого числа сил. Поэтому
предпочтительнее аналитический метод
нахождения равнодействующей. Пусть
система сходящихся сил на плоскости
имеет равнодействующую . Обозначим
Обозначим
через проекции этой равнодействующей
на оси системы координат XOY, а через
проекции сил на те же оси. Из математики
известно, что проекция суммы векторов
на какую – либо ось равна алгебраической
сумме проекций слагаемых векторов на
ту же ось.
Пара
сил
— система
двух сил F1 и F2,
действующих на твёрдое
тело,
равных друг другу поабсолютной
величине,
параллельных и направленных противоположно
друг другу. Пара сил не имеет
равнодействующей, то есть её действие
на тело не может быть
механически эквивалентнодействию
какой-нибудь одной силы; соответственно
пару сил нельзя уравновесить одной
силой.Расстояние r1+r2 между
линиями действия сил пары называется
плечом пары сил. Действие, оказываемое
парой сил на твёрдое тело, характеризуется
её моментом,
который изображается вектором T,
равным по абсолютной величине и
направленным перпендикулярно
кплоскости действия
пары сил в ту сторону, откуда поворот,
совершаемый парой сил, виден происходящим
против хода часовой стрелки (в
правой системе
координат).
Основное свойство пары сил: действие,
оказываемое ею на данное твёрдое тело,
не изменяется, если пару сил переносить
куда угодно в плоскости пары или в
плоскости, ей параллельной, а также если
изменить абсолютную величину сил пары
и длину её плеча, сохраняя неизменным
момент пары сил. Таким образом, момент
пары сил можно считать приложенным к
любой точке тела. Две пары сил с одинаковыми
моментами T,
приложенные к одному и тому же твёрдому
телу, механически эквивалентны одна
другой. Любая система пар сил, приложенных
к данному твёрдому телу, механически
эквивалентна одной паре сил с моментом,
равным геометрической сумме
векторов-моментов этих пар сил. Если
геометрическая сумма векторов-моментов
некоторой системы пар сил равна нулю,
то эта система пар сил является
уравновешенной.
сЛОЖЕНИЕ
ПАР СИЛ. УСЛОВИЕ РАВНОВЕСИЯ ПАР.
Теорема. Система
пар, действующих на тело в одной плоскости,
эквивалентна паре сил с моментом, равным
алгебраической сумме моментов пар
системы.
Допустим,
на тело действуют три пары (рис. а),
моменты которых известны.
Каждую из заданных пар заменим
эквивалентной парой соответственно но
с одинаковыми плечами
т. e.
и расположим эти пары так, чтобы их силы
действовали вдоль двух параллельных
прямых (рис. б).Как
известно, равнодействующая сил,
действующих вдоль одной прямой, направлена
по той же прямой и модуль ее равен
алгебраической сумме составляющих сил.
Поэтому, сложив силы, приложенные к
точкам и
к точкам , , ,
получим равнодействующую пару
эквивалентную трем заданным парам
(рис. в).
При этом .Момент
равнодействующей парыа так как ,
то
или .
Теорема доказана.Распространяя
равенство на
любое число пар, действующих на тело,
можем записать
.Следовательно, для
того чтобы сложить любое число пар,
действующих на тело в одной плоскости,
достаточно алгебраически сложить
моменты этих пар. Полученный в результате
сложения момент и определяет
равнодействующую пару сил.Если в
результате сложения пар ,
то действующие на тело пары образуют
уравновешенную систему. Следовательно,
Следовательно,
необходимое и достаточное условие
равновесия системы пар выражается одним
уравнением
,т.
е. для равновесия системы пар сил,
действующих на тело в одной плоскости,
необходимо и достаточно, чтобы
алгебраическая сумма и
Момент
силы относительно точки и оси
Момент силы
относительно точки О — это вектор, модуль
которого равен произведению модуля
силы на плечо — кратчайшее расстояние
от точки О до линии действия силы.
Направление вектора момента силы
перпендикулярно плоскости, проходящей
через точку и линию действия силы, так,
что глядя по направлению вектора момента,
вращение, совершаемое силой вокруг
точки О, происходит по часовой стрелке.Если
известен радиус-вектор r⃗ точки
приложения силы F⃗ относительно
точки О, то момент этой силы относительно
О выражается следующим образом:Действительно,
модуль этого векторного произведения:В
соответствии с рисунком |r⃗ |sinα=h,
поэтому:Вектор M⃗ O,
как и результат векторного произведения,
перпендикулярен векторам r⃗ и F⃗ ,
которые принадлежат плоскости Π.
Направление вектора M⃗ O таково,
что глядя по направлению этого вектора,
кратчайшее вращение от r⃗ к F⃗ происходит
по часовой стрелке. Другими словами,
вектор M⃗ O достраивает
систему векторов (r⃗ ,F⃗ ) до
правой тройки.Зная координаты точки
приложения силы в системе координат,
начало которой совпадает с точкой О, и
проекцию силы на эти оси координат,
момент силы может быть определен
следующим образом:Момент
силы относительно осиПроекция
момента силы относительно точки на
некоторую ось, проходящую через эту
точку называется моментов силы
относительно оси.Момент силы относительно
оси вычисляется как момент проекции
силы F⃗ на
плоскость Π,
перпендикулярную оси, относительно
точки пересечения оси с плоскостью Π:Знак
момента определяется направлением
вращения, которое стремится придать
телу сила F⃗ Π.
Если, глядя по направлению оси Oz сила
вращает тело по часовой стрелке, то
момент берется со знаком «плюс», иначе
— «минус».
Определить проекцию на ось oy. Проекции векторов на координатные оси. Основные свойства проекций вектора на ось
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O
векторы и . Углом
между векторами и называется наименьший из углов . Обозначается .
Рассмотрим ось l
и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).
Под углом между вектором и осью l
понимают угол между векторами и .
Итак, пусть l
– некоторая ось и – вектор.
Обозначим через A 1
и B 1
проекции на ось l
соответственно точек A
и B
. Предположим,
что A 1
имеет координату x 1
, а B 1
– координату x 2
на оси l
.
Тогда проекцией
вектора на ось l
называется разность x 1
–
x 2
между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l
будем обозначать .
Ясно, что если угол между вектором и осью l
острый, то x 2
>
x 1
, и проекция x 2
–
x 1
> 0; если этот угол тупой, то x 2
x 1
и проекция x 2
–
x 1
l
, то x 2
=
x 1
и x 2
– x 1
=0.
Таким образом, проекция вектора на ось l
– это длина отрезка A 1 B 1
,
взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций
.
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией
данных
векторов называется любой вектор вида , где — некоторые числа. Числа называются
коэффициентами линейной комбинации.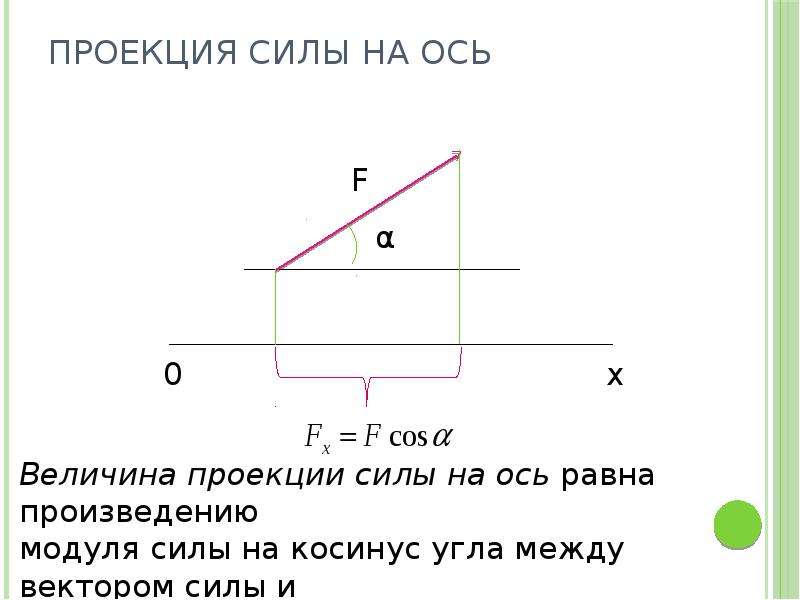 Говорят также, что в этом случае линейно выражается
Говорят также, что в этом случае линейно выражается
через данные векторы , т.е. получается из
них с помощью линейных действий.
Например, если даны три вектора то в качестве
их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то
говорят, что он разложен
по этим
векторам.
Векторы называются линейно зависимыми
, если существуют
такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми,
если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется
только при , эти векторы называются линейно независимыми
.
Теорема 1.
Любые два вектора линейно зависимы тогда и
только тогда, когда они коллинеарны.
Доказательство
:
Аналогично можно доказать следующую теорему.
Теорема 2.
Три вектора линейно зависимы тогда и только тогда,
когда они компланарны.
Доказательство
.
БАЗИС
Базисом
называется совокупность
отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать
.
В предыдущем пункте мы видели, что два неколлинеарных вектора на
плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего
пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой
плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных
вектора. Следовательно, базисом в пространстве назовём три некомпланарных
вектора.
Справедливо следующее утверждение.
Теорема.
Пусть в пространстве
задан базис . Тогда любой вектор можно представить в
виде линейной комбинации , где x
, y
, z
– некоторые числа. Такое разложение единственно.
Доказательство
.
Таким образом, базис позволяет однозначно сопоставить каждому вектору
тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой
Верно и обратное, каждой
тройке чисел x, y, z
при помощи базиса можно сопоставить вектор, если составить
линейную комбинацию .
Если базис и , то числа x, y, z
называются координатами
вектора в данном базисе.
Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O
и три некомпланарных вектора .
Декартовой системой координат
в пространстве (на плоскости) называется совокупность точки и базиса, т.е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка
O
называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются
осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в выбранной системе координат произвольную точку M
. Введём понятие координаты точки M
. Вектор , соединяющий начало координат с точкой M
Вектор , соединяющий начало координат с точкой M
. называется радиус-вектором
точки M
.
Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .
Координаты радиус-вектора точки M
. называются координатами точки M
. в рассматриваемой системе координат. M(x,y,z)
. Первая
координата называется абсциссой, вторая – ординатой, третья – аппликатой.
Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся
единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют
единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.
Несложно показать, что .
Направляющие косинусы вектора полностью
определяют его направление, но ничего не говорят о его длине.
Пусть в пространстве задана ось l, т. е. направленная прямая.
Проекцией точки М на ось l называется основание М 1 перпендикуляра ММ 1 , опущенного из точки на ось.
Точка М 1 есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).
Если точка М лежит на оси l, то проекция точки М на ось совпадает с М1.
Пусть АВ — произвольный вектор (АВ¹ 0). Обозначим через А 1 и b 1 проекции на ось l соответственно начала А и конца В вектора АВ и рассмотрим векторА 1 В 1
Проекцией вектора АВ на ось l называет ся положительное число |A 1 B 1 | , есливектор А 1 В 1 и ось l одинаково направлены и отрица тельное число — |A 1 B 1 | , если вектор А 1 В 1 и ось l противоположно направлены (см. рис. 8). Если точки a 1 и b 1 совпадают (А 1 В 1 =0), то проекция вектора АВ равна 0.
Проекция вектора АВ на ось l обозначается так: пр l
АВ. l , то пр l АВ=0.
l , то пр l АВ=0.
Угол j между вектором а и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно,0£j£p
Рассмотрим некоторые основные свойства проекций.
Свойство 1. Проекция вектора a на ось l равна произведению модуля вектора aна косинус угла j между вектором и осью, т. е. пр l a =|a | cos j .
Следствие 5.1. Проекция вектора на ось положительна (отрицательна), есливектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось
Свойство 3. При умножении вектора а на число А его проекция на ось также умножается на это число, т. е.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
5.4. Разложение вектора по ортам координатных осей.
Модуль вектора. Направляющие косинусы.
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i, j , k соответственно (см. рис. 12).
Выберем произвольный вектор а пространства и совместим его начало с началом координат: а=ОМ.
Найдем проекции вектора а на координатные оси. Проведем через конецвектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М 1 , М 2 и Мз.Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда пр х а=|OM 1 |, np y a = |ОМ 2 |, пр z а=|ОМз|. По определению суммы нескольких векторов находим а = ОМ 1 + M 1 N + NM.
А так как M 1 N=OM 2 , NM =ОМз, то
а=ОМ 1 + ОМ 2 + ОМ 3 (5.1)
Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через а х, а у и a z , т.е. |OM 1 | = а х,|ОМ 2 | = а у, |ОМ 3 | = а z . Тогда из равенств (5. 1) и (5.2) получаем
1) и (5.2) получаем
a=a x i+a y j+a z k (5.3)
Эта формула является основной в векторном исчислении и называетсяразложением вектора по ортам координатных осей. Числа а х, а у, a z называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: a = (a x ;a y ;a z).
Равенство b = (b x ;b y ; b z) означает, что b = b х i +b у j + b z k . Зная проекциивектора а, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора а с осями Ох, Оу и Oz соответственно равны a,b,g. По свойству проекции вектора на ось, имеем
Или, что то же самое,
Числа называются направляющими косинусами вектора а.
Подставим выражения (5.5) в равенство (5. 4), получаем
4), получаем
Сократив на получим соотношение
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора e являются числа
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.
Векторное описание движения является полезным, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения. Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами – проекциями векторов.
Проекцией вектора на ось
называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной координатной оси.
На левом чертеже показан вектор перемещения, модуль которого 50 км, а его направление образует тупой угол
150° с направлением оси X.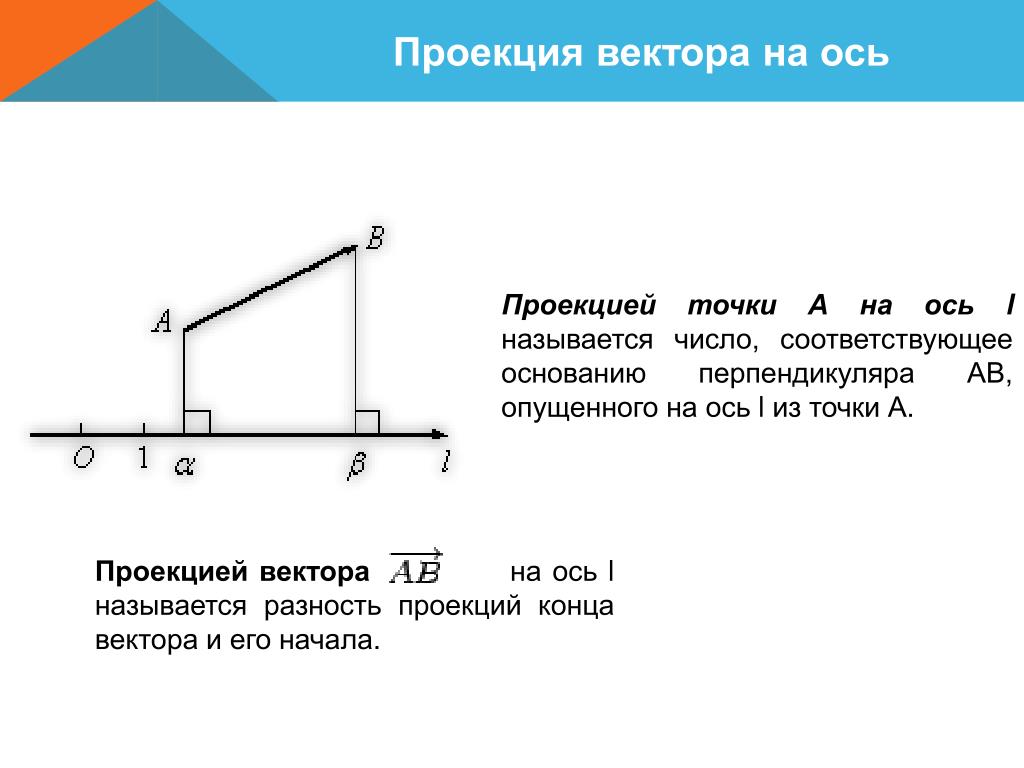 Пользуясь определением, найдём проекцию перемещения на ось X:
Пользуясь определением, найдём проекцию перемещения на ось X:
sx = s · cos(α) = 50 км · cos( 150°) = –43 км
Поскольку угол между осями 90°, легко подсчитать, что направление перемещения образует с направлением оси Y острый угол 60°. Пользуясь определением, найдём проекцию перемещения на ось Y:
sy = s · cos(β) = 50 км · cos( 60°) = +25 км
Как видите, если направление вектора образует с направлением оси острый угол, проекция положительна; если направление вектора образует с направлением оси тупой угол, проекция отрицательна.
На правом чертеже показан вектор скорости, модуль которого 5 м/с, а направление образует угол 30° с направлением оси X. Найдём проекции:
υx = υ · cos(α) = 5 м/c · cos( 30°) = +4,3 м/с
υy = υ · cos(β) = 5 м/с · cos( 120°) = –2,5 м/c
Гораздо проще находить проекции векторов на оси, если проецируемые векторы параллельны или перпендикулярны выбранным осям. Обратим внимание, что для случая параллельности возможны два варианта: вектор сонаправлен оси и вектор противонаправлен оси, а для случая перпендикулярности есть только один вариант.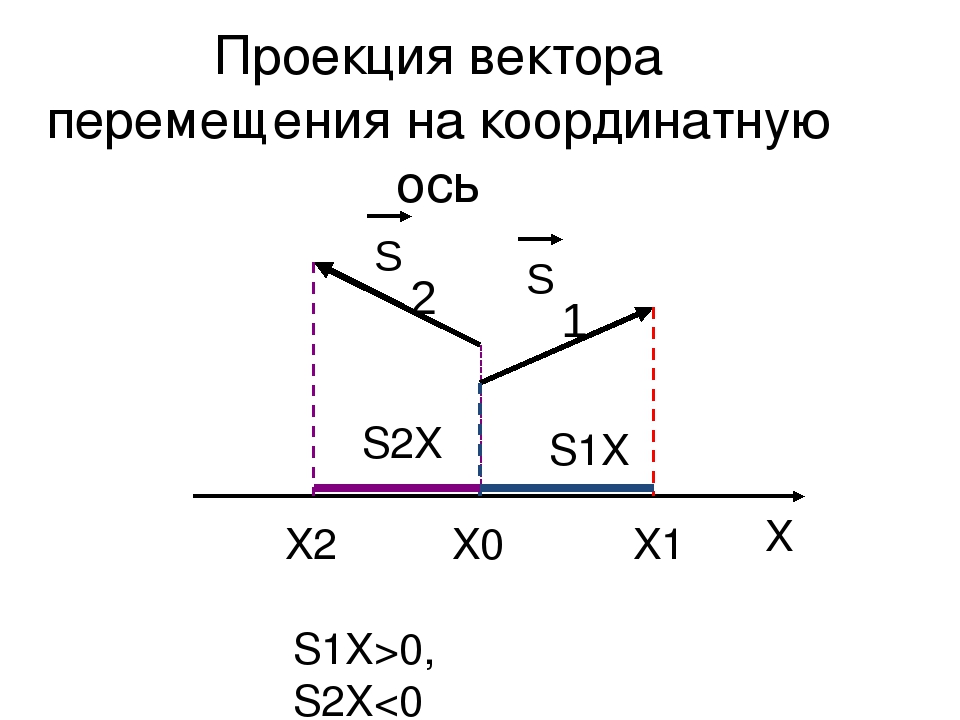
Проекция вектора, перпендикулярного оси, всегда равна нулю (см. sy и ay на левом чертеже, а также sx и υx на правом чертеже). Действительно, для вектора, перпендикулярного оси, угол между ним и осью равен 90°, поэтому косинус равен нулю, значит, и проекция равна нулю.
Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = +s (см. левый чертёж). Действительно, для вектора, сонаправленного с осью, угол между ним и осью равен нулю, и его косинус «+1», то есть проекция равна длине вектора: sx = x – xo = +s .
Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s (см. правый чертёж). Действительно, для вектора, противонаправленного оси, угол между ним и осью равен 180°, и его косинус «–1», то есть проекция равна длине вектора, взятой с отрицательным знаком: sy = y – yo = –s .
На правых частях обоих чертежей показаны другие случаи, когда векторы параллельны одной из координатных осей и перпендикулярны другой. Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.
Предлагаем вам убедиться самостоятельно, что и в этих случаях тоже выполняются правила, сформулированные в предыдущих абзацах.
На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.
Проекция точки
Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А). Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.
Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.
Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).
Как найти длину проекции
Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).
Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.
Проекция скорости
Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.
Проекция вектора
При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот.
Возьмем следующее координатное уравнение: x = x(t), y = y(t), z = z(t). В данном случае функция скорости будет спроецирована на три оси и будет иметь следующий вид: V(x) = dx / dt = x»(t), V(y) = dy / dt = y»(t), V(z) = dz / dt = z»(t). Отсюда следует, что для нахождения скорости необходимо брать производные. Сам же вектор скорости выражается уравнением такого вида: V = V(x) i + V(y) j + V(z) k. Здесь i, j, k являются единичными векторами координатных осей x, y, z соответственно. 2).
2).
§ 3.
Проекции вектора на оси координат
1.
Нахождение проекций геометрически.
Вектор
— проекция вектора
на ось OX
— проекция вектора
на ось OY
Определение
1.
Проекцией вектора
на какую-либо ось
координат называется взятое со
знаком «плюс» или «минус»
число, соответствующее длине отрезка,
расположенного между основаниями
перпендикуляров, опущенных из начала
и конца вектора на ось координат.
Знак
проекции определяется так. Если при
движении вдоль оси координат
происходит перемещение от точки
проекции начала вектора к точке
проекции конца вектора в положительном
направлении оси, то проекция вектора
считается положительной. Если же —
противоположно оси, то проекция
считается отрицательной.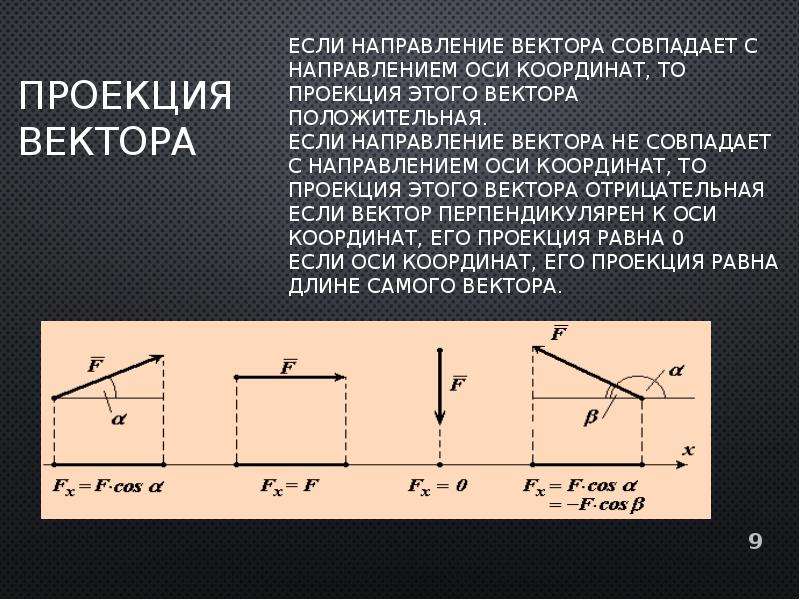
По
рисунку видно, что если вектор
ориентирован как-то противоположно оси
координат, то его проекция на эту ось
отрицательна. Если вектор ориентирован
как-то в положительном направлении оси
координат, то его проекция на эту ось
положительна.
Если
вектор перпендикулярен оси координат,
то его проекция на эту ось равна нулю.
Если вектор сонаправлен с осью,
то его проекция на эту ось равна модулю
вектора.
Если вектор противоположно
направлен оси координат, то его
проекция на эту ось по абсолютной
величине равна модулю вектора, взятому
со знаком минус.
2. Наиболее
общее определение проекции.
Из прямоугольного
треугольника ABD
: .Определение
2.Проекцией вектора
на какую-либо
ось координат называется число,
равное произведению модуля вектора и
косинуса угла, образованного
вектором с положительным
направлением оси координат.
Знак
проекции определяется знаком косинуса
угла, образованного вектором с
положительным направлением оси.
Если угол острый, то косинус
имеет положительный знак, и проекции —
положительны. Для тупых углов косинус
имеет отрицательный знак, поэтому в
таких случаях проекции на ось
отрицательны.
—
поэтому для векторов, перпендикулярных
к оси, проекция равна нулю.
Техническая механика. Теоретическая механика | ПроСопромат.ру
Часто геометрическое сложение векторов сил требует сложных и громоздких построений. В таких случаях прибегают к другому методу, где геометрическое построение заменено вычислениями скалярных величин. Достигается это проектированием заданных сил на оси прямоугольной системы координат.
Как известнее из математики, осью называют неограниченную прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными из начала и конца вектора на ось.
Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными из начала и конца вектора на ось.
Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (—), если направление от начала проекции к ее концу противоположно положительному направлению оси.
Рассмотрим ряд случаев проектирования сил на ось.
- Дана сила Р (рис.а), она лежит в одной плоскости с осью х. Вектор силы составляет с положительным направлением оси острый угол α.
Чтобы найти величину проекции, из начала и конца вектора силы опускаем перпендикуляры на ось х, получаем
Рх = ab = Р cos α.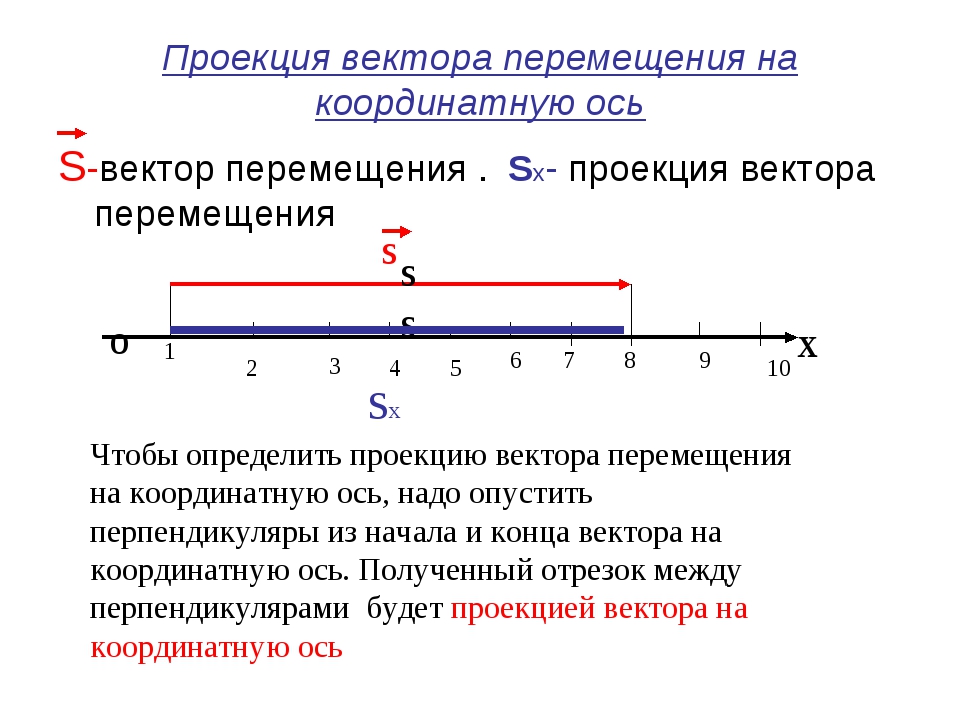
Проекция вектора в данном случае положительна.
2. Дана сила Q (рис. б), которая лежит в одной плоскости с осью х, но ее вектор составляет с положительным направлением оси тупой угол α.
Проекция силы Q на ось х
Qх = ab = Q cos α,
но
cos a = — cos β.
Так как α > 90°, то cos cos α — отрицательная величина. Выразив cos α через cos β (β — острый угол), окончательно получим
Qх = — Q cos β
В этом случае проекция силы отрицательна.
Итак, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.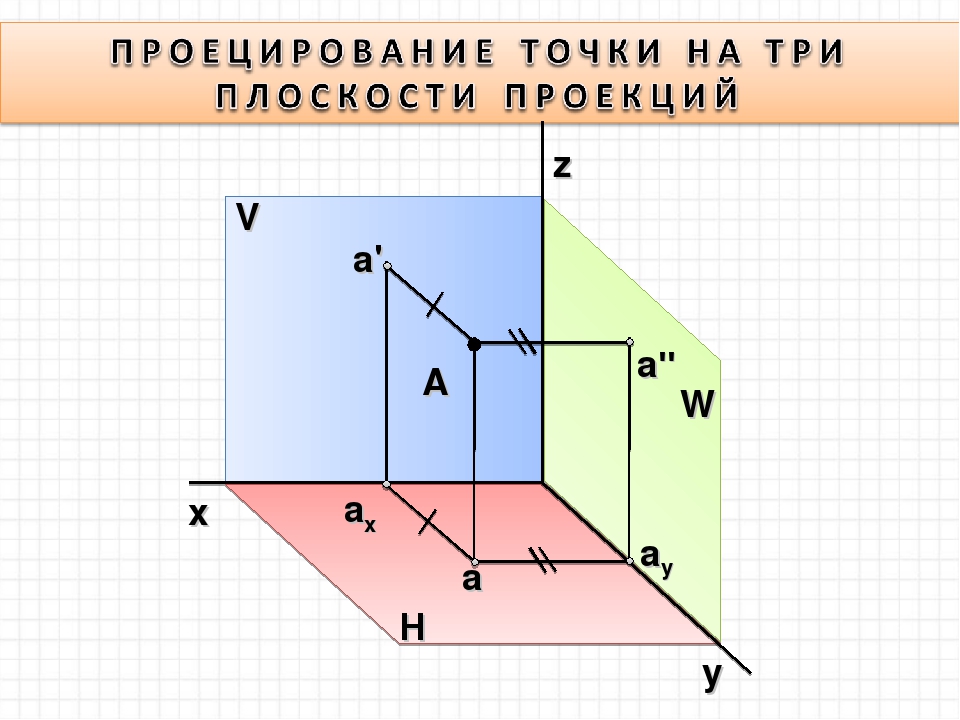
При определении проекции вектора силы на ось пользуются обычно косинусом острого угла, независимо от того, с каким направлением оси — положительным или отрицательным — он образован. Знак проекции легче устанавливать непосредственно по чертежу.
Силу, расположенную на плоскости хОу, можно спроектировать на две координатные оси Ох и Оу. Рассмотрим рисунок.
На нем изображена сила Р и ее проекции Рх и Ру. Ввиду того что проекции образуют между собой прямой угол, из прямоугольного треугольника ABC следует:
Этими формулами можно пользоваться для определения величины и направления силы, когда известны ее проекции на координатные оси.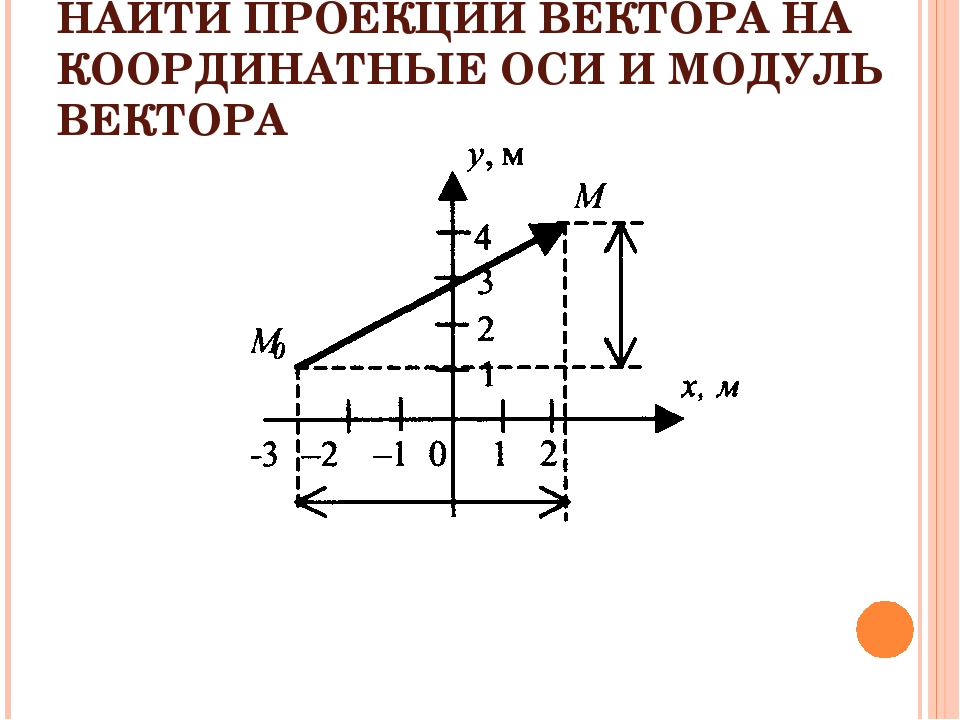 Эти же формулы могут применяться для определения величины и направления любого вектора через его проекции.
Эти же формулы могут применяться для определения величины и направления любого вектора через его проекции.
Почему скалярное произведение представляет собой длину проекции на * единичный * вектор?
Это действительно сводится к давнему вопросу о том, «что является лучшим интуитивным пониманием скалярного произведения», который, по общему признанию, не является загадкой для многих, поскольку он очень часто возникает.
Что я бы сказал относительно этого вопроса — и который, таким образом, также отвечает на вопрос в вашем заголовке, — так это то, что скалярное произведение является «математически уточненной» версией операции проекции: а именно, интуиция подсказывает, что $ \ mathbf {a } \ cdot \ hat {\ mathbf {u}} $ для единичного вектора $ \ hat {\ mathbf {u}} $ действительно является компонентом $ \ mathbf {a} $ в направлении $ \ hat {\ mathbf {u}} $, и мы могли бы начать построение скалярного произведения оттуда.
Конечно, возникает вопрос, что делать, если $ \ mathbf {u} $ — это , а не единичный вектор.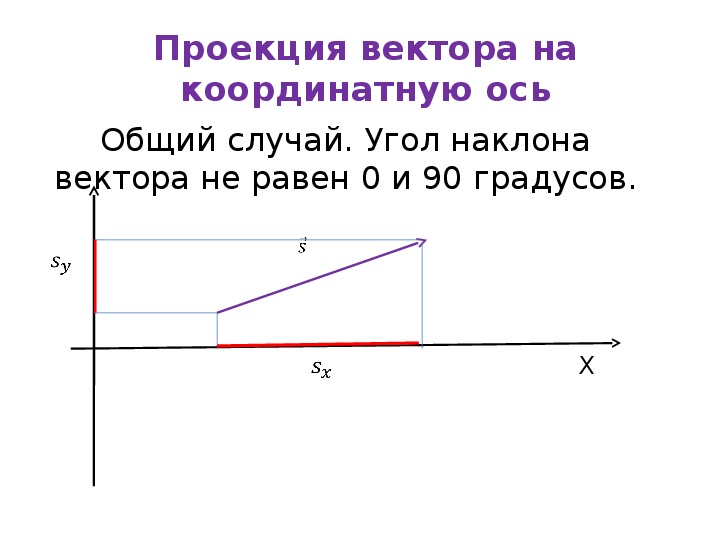 Один из вариантов — просто сказать, что это не имеет значения: в любом случае просто укажите проекцию (компонент) в нужном направлении. Однако это приводит к некоторым проблемам. Во-первых, давайте рассмотрим коммутативность. В идеале у нас было бы , как , если бы наш продукт был коммутативным:
Один из вариантов — просто сказать, что это не имеет значения: в любом случае просто укажите проекцию (компонент) в нужном направлении. Однако это приводит к некоторым проблемам. Во-первых, давайте рассмотрим коммутативность. В идеале у нас было бы , как , если бы наш продукт был коммутативным:
$$ \ mathbf {a} \ cdot \ hat {\ mathbf {u}} = \ hat {\ mathbf {u}} \ cdot \ mathbf {a} $$
, однако, если мы спустимся вниз по строке описания, которую я только что дал, и просто скажем, что он дает проекцию на второй операнд как чистый индикатор направления, то мы имеем асимметричную некоммутативную операцию.
Однако, к счастью, оказалось, что эти проблемы исчезнут, если мы решим, что
$$ \ mathbf {a} \ cdot \ mathbf {u} $$
, когда $ \ mathbf {u} $ — это , а не единичный вектор, должно быть проекцией , масштабированной на длину вектора проекции , здесь $ \ mathbf {u} $. Учитывая, что проекция уже масштабируется на длину вектора , проецируемого , по сути, это приводит к тому, что оба вектора обрабатываются «на равных основаниях», так сказать, и теперь операция коммутируется.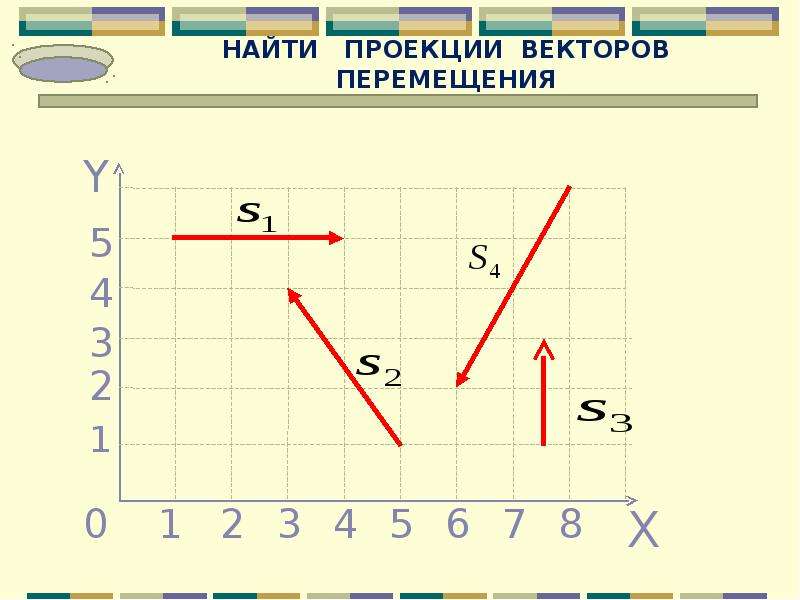 Более того, он становится даже билинейным , что даже лучше, и, таким образом, превращает его в тензор (возможно, даже канонический пример!), Что позволяет делать всевозможные обобщения в более сложных математических целях, включая возможность определять римановы многообразия. и поговорим о криволинейных, неевклидовых пространствах, а также о возможности предоставить бесконечномерные пространства с полезными топологическими структурами, допускающими такие вещи, как бесконечные линейные комбинации, как мы получаем, когда спускаемся вниз по последовательности внутреннего пространства продукта.
Более того, он становится даже билинейным , что даже лучше, и, таким образом, превращает его в тензор (возможно, даже канонический пример!), Что позволяет делать всевозможные обобщения в более сложных математических целях, включая возможность определять римановы многообразия. и поговорим о криволинейных, неевклидовых пространствах, а также о возможности предоставить бесконечномерные пространства с полезными топологическими структурами, допускающими такие вещи, как бесконечные линейные комбинации, как мы получаем, когда спускаемся вниз по последовательности внутреннего пространства продукта.
Короче говоря, скалярное произведение представляет проекцию на единичный вектор , потому что в этой точке коэффициент масштабирования, который мы вводим, чтобы сделать его математически «красивым» и «беспристрастным», равен 1 доллару, когда вектор проекции таков.
Векторная проекция | Суперпроф
Независимо от того, являетесь ли вы инженером или астрологом, вам все равно необходимо понимать, как проецируются векторы, чтобы определить величину, а также направление силы, приложенной к любому объекту.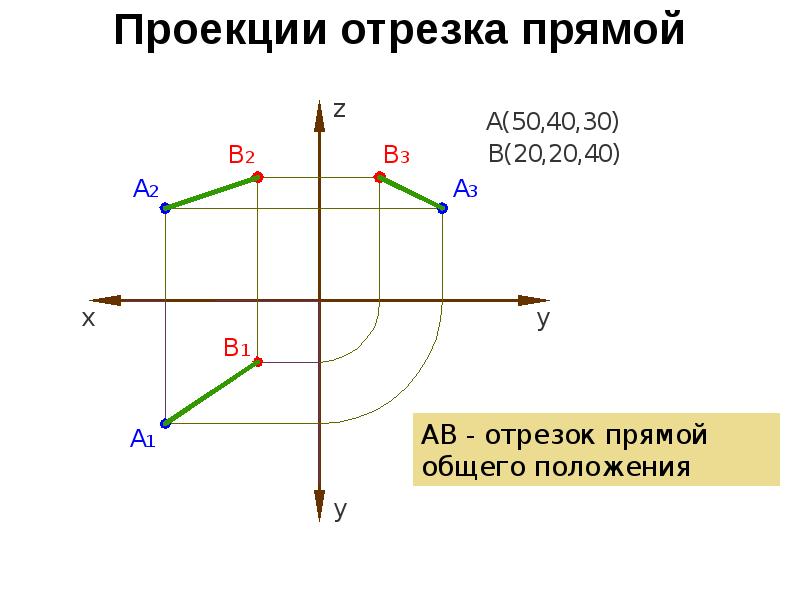 Эта ценная информация может помочь нам найти различные наборы данных, такие как скорость, тепло, сила, направление и многое другое. Проецирование вектора в другой — одна из основ физики и математики. Без проекции векторов невозможно определить природу силы, и это может привести ко многим ошибкам. Чтобы избежать этих ошибок, ученые нашли способ выяснить истинную природу силы и как они это сделали? Путем проецирования векторов. В этом уроке вы узнаете о двух разных векторных проекциях.
Эта ценная информация может помочь нам найти различные наборы данных, такие как скорость, тепло, сила, направление и многое другое. Проецирование вектора в другой — одна из основ физики и математики. Без проекции векторов невозможно определить природу силы, и это может привести ко многим ошибкам. Чтобы избежать этих ошибок, ученые нашли способ выяснить истинную природу силы и как они это сделали? Путем проецирования векторов. В этом уроке вы узнаете о двух разных векторных проекциях.
Скалярная проекция
Скалярная проекция — это в основном величина проекции вектора. Чтобы понять скалярную проекцию, вам нужно знать о скалярном произведении. Скалярное произведение любых двух векторов дает скалярную величину, которая описывает длину (величину) конкретного вектора. Тогда возникает вопрос, что такое скалярная проекция? Это проекция, когда вы скалярно произведение единичного вектора на вектор в определенном направлении.
Если скалярная проекция дает положительное значение, это означает, что угол между обоими векторами меньше 90∘.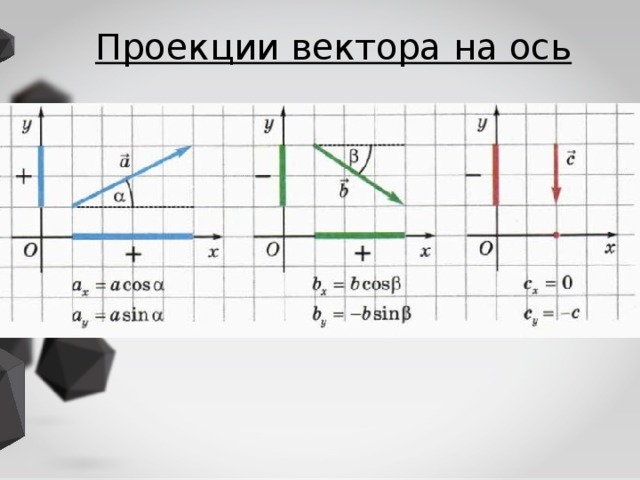 Это также означает, что оба вектора направлены в одном направлении. С другой стороны, если скалярная проекция дает отрицательное значение, это означает, что угол между обоими векторами больше 90∘. Это также говорит нам о том, что векторы направлены в противоположные стороны.
Это также означает, что оба вектора направлены в одном направлении. С другой стороны, если скалярная проекция дает отрицательное значение, это означает, что угол между обоими векторами больше 90∘. Это также говорит нам о том, что векторы направлены в противоположные стороны.
Лучшие преподаватели по математике
Первый урок бесплатно
Проекция вектора
Один из наиболее часто задаваемых вопросов: почему мы проецируем один вектор на другой? Чтобы определить, насколько вектор равен другому вектору в том же направлении.Проекция вектора — это единичный вектор
путем скалярной проекции u на v. На математическом языке это записывается как. Это означает, что вектор «v» проецируется на «u». Проще говоря, новый вектор проецируется и в направлении u. Векторная проекция часто используется в физике и математике. Причина в том, что он используется для решения различных сил, действующих на разные тела по отношению к его составляющим векторам. На этом этапе вы можете быть сбиты с толку, поэтому давайте сделаем это просто.Вектор в любом направлении имеет две компоненты: одна параллельна второму вектору, а другая перпендикулярна второму вектору. В физике мы не используем второй вектор как систему отсчета, мы используем ось как систему отсчета. Оси — абсцисса и ордината. Ось X называется компонентом, а ось Y — компонентом. Проще говоря, концепция векторной проекции такая же, но система отсчета другая.
На этом этапе вы можете быть сбиты с толку, поэтому давайте сделаем это просто.Вектор в любом направлении имеет две компоненты: одна параллельна второму вектору, а другая перпендикулярна второму вектору. В физике мы не используем второй вектор как систему отсчета, мы используем ось как систему отсчета. Оси — абсцисса и ордината. Ось X называется компонентом, а ось Y — компонентом. Проще говоря, концепция векторной проекции такая же, но система отсчета другая.
Например, вы пытаетесь поднять ящик под определенным углом.Направление, в котором вы поднимаете ящик, можно решить двумя способами. Проще говоря, общая сила, которую вы прикладываете к коробке, состоит из двух частей. Один — это сила тяги, а другой — подъемная сила. Это можно решить с помощью векторной проекции. Часть общей силы тратится на подъем коробки из одной точки в другую, а оставшаяся часть силы тратится на перетягивание коробки из одной точки в другую. Общая сила будет суммой подъемной и тянущей сил и будет записана так:
и — проекции вектора на вектор полной силы. Проекция вектора — это единичный вектор скалярной проекции u на v.
Проекция вектора — это единичный вектор скалярной проекции u на v.
Скалярная проекция u на v — это величина проекции вектора u на v.
Примеры
Вычислить проекция вектора
на вектор.
Вычислить проекцию вектора
на вектор.
Вычислить скалярную проекцию вектора
на вектор, если: и.
Если вершины треугольника равны
и, вычислите скалярные проекции сторон AB и CB на AC и убедитесь, что их сумма равна длине AC.
Мир в негативной проекции — Карен Вудалл:
Это определение проекции взято из APA
Негативная проекция — мощная динамика в семьях, пострадавших от отчуждения.Это мощная динамика, окружающая и эти семьи, и любой, кто рискнет войти в это пространство, должен понять, что это такое и как проявляется. Негативная проекция — это механизм, с помощью которого кто-то отделяет части своего осознания себя и проецирует эти части, видя в других то, что они не могут увидеть в себе.
Негативная проекция — это механизм, с помощью которого кто-то отделяет части своего осознания себя и проецирует эти части, видя в других то, что они не могут увидеть в себе.
Негативная проекция в случаях отчуждения часто встречается в профессиональной команде вокруг семьи. У него есть динамика, которая узнаваема в том, что у команды часто бывает разное мнение о семье, с которой она работает, считая других в команде неправыми.
Негативная проекция наблюдается в группах кампании, где люди, участвующие в кампании, рассматривают других как врагов, а себя как жертв другой группы или системы.
Негативная проекция — это опасная динамика, и поэтому, как родителю или профессионалу, работающему в этой области, важно понять ее, распознать и научиться справляться с ней и работать с ней. Не со всеми случаями негативной проекции нужно будет работать, некоторые можно просто оставить наедине с собой (например, когда кто-то решил, что вы являетесь причиной всех его проблем и что у кого-то нет власти чтобы навредить вам каким-либо образом), другие потребуют, чтобы вы разобрались с этим напрямую (когда кто-то использует свои негативные прогнозы, чтобы попытаться добиться разрушительных результатов в вашей жизни).
Ребенок, страдающий индуцированным психологическим расщеплением, получает проекции влияющего родителя, а также проекции отвергаемого родителя. Это ужасное место для ребенка, и если вы отвергнутый родитель, совершенно необходимо, чтобы вы понимали, что ваши проекции на вашего ребенка или другого его родителя усилят защиту ребенка от расщепления. Поэтому важно избегать проецирования, потому что это одна из ключевых защит, используемых при сознательном или бессознательном влиянии на родителей, и по определению этот родитель вряд ли сможет отказаться от своих проекций.
Проекции — это те чувства, которые мы не можем испытать в себе, поэтому мы разделяем их, отрицаем их наличие, а затем проецируем их на других людей или группы людей. Считается, что проекции сильно влияют на группы, основанные на правах, аргумент о том, что вы отняли мои права, проецируется на другого человека или группу людей. Это происходит из-за того, что вина за чувство беспомощности и бессилия должны быть возложены на кого-то другого, потому что чувства слишком сильны, чтобы их вынести. Результатом защиты является то, что обвиняющий чувствует себя сильным в этом действии. Любой, кто тратит свое время на то, чтобы говорить другим, что они неправы и виноваты в причинении вреда, в то же время будучи не в состоянии признать, что они используют тактику контроля и власти, предназначенную для нанесения вреда получателю проекции, использует защиту проекции и, как таковой, не может полностью понять, что этим они причиняют другим вред.
Результатом защиты является то, что обвиняющий чувствует себя сильным в этом действии. Любой, кто тратит свое время на то, чтобы говорить другим, что они неправы и виноваты в причинении вреда, в то же время будучи не в состоянии признать, что они используют тактику контроля и власти, предназначенную для нанесения вреда получателю проекции, использует защиту проекции и, как таковой, не может полностью понять, что этим они причиняют другим вред.
Мир не делится на хорошее и плохое, черное и белое, позитивное и негативное.Как бы легко ни было так думать и чувствовать, это не разделено таким образом. В мире после разлуки, где эмоциональная и психологическая декомпенсация приносит с собой огромное количество страха, обычным результатом является разделение на хорошее и плохое, отрицание плохого в себе и видение его только в других. Он хорошо воспроизводит то, что происходит с детьми в ситуациях, когда они страдают от отчуждения. Когда эта динамика проявляется в семье, неудивительно, что детей заставляют использовать эту защиту.
Наиболее поразительные примеры разделения — это группы кампаний по защите родительских прав, и именно здесь мы видим зеркальное отражение прогнозов друг друга.Это настолько яркий пример проекции, что один и тот же предмет виден в каждой группе только в обратном направлении.
Например, группы кампаний вокруг судов по семейным делам заполнены кабинетными психологами, которые определяют, что любой, кто не является феминисткой, является активистом по защите прав мужчин, имеющим проблемы с мамой, или, наоборот, кабинетными психологами, которые считают, что у всех феминисток есть проблемы с отцами. Эти группы анализируют своих врагов и болтают между собой о том, что другая сторона — настоящий злодей.Обвинение и осуждение жертв, защита жертв и их идеализация широко распространены на этой арене, что заставляет меня задаться вопросом, что испытывают дети из этих семей. Как бы то ни было, оно не сбалансировано, и поэтому проекции как защитного механизма следует избегать в ситуациях, когда ребенок отчужден.
Потому что, если все, что вы делаете как отвергнутый родитель, — это копируете поведение отчуждающего, если все, что вы делаете, это общаетесь с людьми, которые заняты обвинением других, тогда все ваши дети когда-либо получат, это больше похоже на то, что вызвало проблема в первую очередь.Если вы хотите иметь возможность помочь своему ребенку, держитесь подальше от негативных проекций и научитесь замечать их и работать с ними или отступать от них, когда вам нужно.
Вы будете знать, когда кто-то делает негативные прогнозы, потому что они будут видеть в вас всю проблему. Негативная проекция заставляет людей делать то, чего не делают обычные хорошо уравновешенные люди. Проекция может подтолкнуть людей к навязчивому, злому поведению, выходящему за рамки нормальности. Это может вызвать убеждение в том, что вы открыли правду о себе, и побуждение заставить других поверить в то же самое.
Негативные проекции обладают огромным количеством навязчивой энергии, потому что потребность защищать себя у проектируемого человека огромна. Люди, которые проводят время, обвиняя и стыдя других, на самом деле очень стыдятся самих себя. Чем сильнее проекция, тем глубже стыд. Помните, что в следующий раз вы увидите, как кто-то лжет о вас, устраивает кампании очернения или заставляет ваших детей и других вести себя так, как будто вы монстр. История травмы в проецировании вины состоит в том, что человек, который это делает, скрывает от себя что-то настолько чудовищное, что вынужден заставить других поверить в чудовищные вещи о вас.
Люди, которые проводят время, обвиняя и стыдя других, на самом деле очень стыдятся самих себя. Чем сильнее проекция, тем глубже стыд. Помните, что в следующий раз вы увидите, как кто-то лжет о вас, устраивает кампании очернения или заставляет ваших детей и других вести себя так, как будто вы монстр. История травмы в проецировании вины состоит в том, что человек, который это делает, скрывает от себя что-то настолько чудовищное, что вынужден заставить других поверить в чудовищные вещи о вас.
Здоровым людям не нужно отрицать, разделять и проецировать. Здоровые люди осведомлены о менее здоровых частях своего «я» и работают над их пониманием, а также о том, как они могут привести эти части к более целостному здоровью. Работая из уравновешенного места в качестве отвергнутого родителя, вы не почувствуете необходимости собираться в группы и присоединяться к толпе, вы найдете больший покой в работе над собственным пониманием себя и построении твердой платформы для ваших детей. вернуться домой.
Прямо сейчас, на Диком Западе Интернета, существует множество негативных прогнозов, которые возникают и падают вместе с коллективными волнами гнева от нездоровых людей. Есть одинокие рейнджеры, катающиеся на волнах Wi-Fi с мыслями о заданиях, и группы, которые выкатывают шокирующие мемы. Есть люди, которые утверждают, что с их тысячами последователей они могут навсегда изменить ваш мир, и люди, которые скажут вам, что все остальные продают змеиное масло (что бы это ни было). В то же время эти люди скажут вам, что другие причинят вам вред, что они злые и злые, и будут шептать о теориях заговора и связях с дьяволом.Это мир пограничного поведения, проводить в нем слишком долго — вредно.
Чтобы быть в безопасности, необходимо сильное чувство собственного достоинства и способность распознавать негативные проекции. Две вещи, которыми отвергнутые родители редко обладают в начале своего пути, но которым они должны быстро научиться.
Первое правило, как справиться с неприятием вашего ребенка, заключается в том, что вы ничему не научитесь, крича с толпой на ветер. Все, что произойдет, это то, что вы услышите отголоски собственного отчаяния и негативные проекции, возвращающиеся к вам с другой стороны.Это игра в теннис с негативными проекциями, это бессмысленная трата времени. Те, у кого более здоровый образ мышления, быстро это поймут. Остальные будут тратить свое время, пытаясь выиграть игру, в которой никогда не выиграть, потому что игроки заняты защитой своей собственной неспособности принять хорошее и плохое в самих себе.
Что нужно жить, когда вы обнаруживаете себя назначенным отвергнутым родителем в ситуации, когда нездоровый родитель вызывает гипер-выравнивание с вашим ребенком —
- Жизнь не делится на хорошую и плохую.
- Хорошие люди иногда делают плохие поступки.
- Вы не приносите миру здоровье через вину и позор.
- Мы все несем ответственность за собственное благополучие.
- У всех нас есть собственный внутренний ребенок, о котором нужно заботиться.
Дайте своему внутреннему ребенку передышку и держитесь подальше от толпы. Слушайте, учитесь и любите своего внутреннего ребенка, когда вы это сделаете, он / она вернет вам то, что вам нужно, чтобы построить жизнь, полную честности и здоровья.
Поступая так, вы будете строить для своего внешнего ребенка путь, по которому они будут идти домой.Путь, который больше не омрачен негативными проекциями.
Дорожка, ведущая прямо к вашей двери.
На пути к возвращению домой — мастерская для родителей
Семинар для родителей будет проведен в рамках конференции EAPAP 2020. Этот семинар, посвященный здоровым стратегиям выздоровления отчужденных детей, будет проводиться Карен Вудалл и Ником Вудаллом и будет основан на работе, проделанной в отделении семейного разлучения. Клиника, в которой основное внимание уделяется лечению детей, страдающих индуцированным психологическим расщеплением.
Этот семинар, основанный на успешных услугах клиники, которые предоставляются с использованием психоаналитической модели понимания и вмешательства с учетом травм, предназначен для всех отвергнутых родителей, которые хотят построить здоровое будущее для своих детей.
Книга для конференции и семинара Здесь
Четверг 6 августа 2020 16:00 — 18:00 (GMT)
Проверьте местное время здесь: Конвертер часовых поясов
Основная проблема отчуждения родителей — это защита психологического расщепления.Это рефлексивная защита ребенка, которая вступает в игру, когда ребенок не может справиться с динамикой вокруг ребенка.
Индуцированное психологическое расщепление приводит к тому, что ребенок отчуждается сначала от собственного самоощущения, а затем от отношений во внешнем мире. Результатом этого является отрицание и проецирование на родителей раздвоенного самоощущения.
Понимание того, как ведут себя дети, когда они психологически расщепляются, важно, потому что это позволяет нам понять, как им реагировать.То, что кажется странным, на самом деле легко распознать и отреагировать, когда распознается защита. Помощь детям в интеграции тех частей личности, которые они отщепили и отрицают, является ключевой частью их выздоровления.
Это занятие подходит для родителей и практикующих врачей и предлагает введение в понимание отчужденных детей, которое будет охватывать динамику, вызывающую отчуждение, различные способы концептуализации проблемы, подробный анализ нарушения привязанности, которое вызывает проблема, и введение в как эффективно реагировать на это в воспитании детей или практике с отчужденными детьми.
ВАЖНО:
- Этот вебинар будет проводиться на Zoom.
- Чтобы получить доступ, вы должны предоставить действующий адрес электронной почты вместе с вашим именем и номером заказа PayPal (вы получите его по электронной почте от PayPal после совершения платежа).
Нравится:
Нравится Загрузка …
Связанные
% PDF-1.6
%
296 0 объект
>
эндобдж
xref
296 113
0000000016 00000 н.
0000003758 00000 н.
0000003967 00000 н.
0000004096 00000 н.
0000004132 00000 н.
0000004439 00000 н.
0000004667 00000 н.
0000004813 00000 н.
0000004835 00000 н.
0000004994 00000 н.
0000005141 00000 п.
0000005163 00000 п.
0000005321 00000 п.
0000005466 00000 н.
0000005488 00000 н.
0000005645 00000 н.
0000005792 00000 н.
0000005814 00000 н.
0000005969 00000 н.
0000006116 00000 п.
0000006138 00000 п.
0000006296 00000 н.
0000006441 00000 н.
0000006463 00000 н.
0000006618 00000 н.
0000006763 00000 н.
0000006785 00000 н.
0000006941 00000 п.
0000007088 00000 н.
0000007110 00000 н.
0000007264 00000 н.
0000007411 00000 п.
0000007433 00000 н.
0000007765 00000 н.
0000007868 00000 н.
0000007970 00000 п.
0000008007 00000 н.
0000009571 00000 н.
0000011099 00000 п.
0000012649 00000 п.
0000012843 00000 п.
0000014028 00000 п.
0000018171 00000 п.
0000018670 00000 п.
0000018875 00000 п.
0000020388 00000 п.
0000021571 00000 п.
0000022576 00000 п.
0000023605 00000 п.
0000023791 00000 п.
0000023985 00000 п.
0000024166 00000 п.
0000025142 00000 п.
0000025642 00000 п.
0000025841 00000 п.
0000033594 00000 п.
0000033936 00000 п.
0000034458 00000 п.
0000034659 00000 п.
0000042291 00000 п.
0000042654 00000 п.
0000043838 00000 п.
0000044505 00000 п.
0000045483 00000 п.
0000047125 00000 п.
0000047573 00000 п.
0000047685 00000 п.
0000049587 00000 п.
0000049774 00000 п.
0000050216 00000 п.
0000051400 00000 п.
0000052584 00000 п.
0000053767 00000 п.
0000054635 00000 п.
0000054846 00000 п.
0000059723 00000 п.
0000059923 00000 п.
0000060457 00000 п.
0000060577 00000 п.
0000060766 00000 п.
0000062204 00000 п.
0000063185 00000 п.
0000064369 00000 н.
0000064461 00000 п.
0000065081 00000 п.
0000065269 00000 п.
0000065698 00000 п.
0000067031 00000 п.
0000068440 00000 п.
0000071133 00000 п.
0000074222 00000 п.
0000079319 00000 п.
0000079820 00000 н.
0000080205 00000 п.
0000080413 00000 п.
0000080836 00000 п.
0000081022 00000 п.
0000082584 00000 п.
0000082766 00000 н.
0000082879 00000 п.
0000104757 00000 н.
0000104796 00000 н.
0000105752 00000 н.
0000105805 00000 н.
0000109171 00000 п.
0000109234 00000 п.
0000109664 00000 н.
0000109797 00000 п.
0000109921 00000 н.
0000110063 00000 н.
0000110207 00000 н.
0000110431 00000 н.
0000002556 00000 н.
трейлер
] / Назад 4 >>
startxref
0
%% EOF
408 0 объект
> поток
h ެ TmL [U ~ oKWJalDtd @ ICJ:
Cq1 ٬ S: (Zja) hqMml8S1 ~ Ye11I = 9
Как родительская проекция влияет на детей
Что ваш ребенок говорит вам? Общие сведения о проекции
Через проекцию наши внутренние конфликты могут отражаться на нас через других.Давайте посмотрим, как опыт родителей может спроецироваться на их детей как в хорошем, так и в плохом смысле.
Общие сведения о проекции
Психологическая проекция — это своего рода защитный механизм, который заставляет нас приписывать характеристики, которые мы считаем неприемлемыми в себе, кому-то другому. В то же время бывают случаи, когда человек может проецировать свои положительные качества на другого человека.
Проекция может играть скрытую роль во всех наших отношениях.Это может вызвать у нас неприязнь к коллеге, чьи негативные характеристики похожи на наши собственные. Это может заставить нас идеализировать романтического партнера, вызывая неконтролируемое или даже опасное увлечение. С точки зрения родителей, проекция может быть особенно вредной, потому что она может побуждать детей принимать убеждения и поведение в попытке «жить дальше» или «жить вниз» в соответствии с проецируемой идентификацией.
Возьмем, к примеру, этот суровый пример матери, которая выросла с ощущением, будто она никогда не сможет достичь своих целей или утвердиться среди сверстников.Эта мать может сказать дочери, что жизнь несправедлива, и ей не стоит рассчитывать на многое.
Это не что иное, как очевидное предположение, поскольку именно мать, а не ребенок чувствует себя неудачницей. Не в силах справиться со своими чувствами, мать бессознательно передает их дочери. После долгих лет слышания такого рода негативных проекций дочь может начать действовать в соответствии с ними, как если бы они точно ее описывали.
Это подчинение спроецированной идентичности особенно трагично, потому что оно фактически лишает ребенка его собственной идентичности и потенциального будущего.Может показаться, что ребенок должен уметь распознавать, что слова матери — всего лишь отражение ее собственного жизненного опыта. К сожалению, дети обычно не могут дать такую оценку. Вместо этого они склонны включать эти прогнозы — по крайней мере, так или иначе — в свою собственную идентичность
Даже когда дети способны отвергать негативные прогнозы, проблема имеет тенденцию вызывать конфликт между ними и их родителями. Во многих случаях обида укореняется, и дети могут расти с сильным желанием уйти из дома и разорвать отношения с родителями.
Может ли проекция быть положительной?
В некоторых случаях проекция может подтолкнуть детей увидеть себя в положительном свете. Родитель с высокими достижениями может неосознанно проецировать на ребенка амбиции и уверенность, помогая сформировать более позитивное представление о себе, что в конечном итоге приводит к успеху. Однако столь же часто это может проявляться в виде чрезмерного давления, которое может привести к тому, что ребенок почувствует разочарование из-за того, что не оправдал ожиданий родителей.
Что вы можете сделать
Поскольку обычно это бессознательные побуждения, родители нередко делают прогнозы, которые навязывают детям свои нерешенные проблемы.Самые любящие родители могут проецировать на своих детей страхи, разочарования, предубеждения и ожидания, даже не подозревая об этом. Даже в самых благоприятных обстоятельствах это может повлиять на развитие детей, заставляя детей принимать личности, которые на самом деле могут не принадлежать им.
Если вы подозреваете, что проецируете на ребенка свои собственные проблемы, сделайте шаг назад и честно оцените свои слова и поведение. Подумайте о собственном детстве и попытайтесь понять, переняли ли вы проекции своих родителей в своей личности.Наконец, если у вас есть нерешенные проблемы, подумайте о том, чтобы обратиться к терапевту, который поможет вам с ними справиться. Это может помочь вам выйти из цикла проекций и достичь лучшего общего состояния благополучия.
Foundations здесь, чтобы помочь вам и вашей семье справиться с серьезными жизненными изменениями и повседневными проблемами. Свяжитесь с нашим офисом для получения бесплатной консультации!
Умножение векторов — Гипертекст по физике
Обсуждение
умножение скалярных векторов
Умножение вектора на скаляр изменяет величину вектора, но оставляет его направление неизменным.Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, вектор полярной формы…
r = r r̂ + θ θ̂
, умноженное на скаляр , равно…
a r = ar r̂ + θ θ̂
Умножение вектора на скаляр является дистрибутивным.
a ( A + B ) = a A + a B
Следовательно, вектор прямоугольной формы…
r = x î + y ĵ
, умноженное на скаляр , равно…
a r = ax î + ay ĵ
скалярное произведение
Геометрически скалярное произведение двух векторов — это величина, умноженная на проекцию второго на первый.
Символ, используемый для представления этой операции, представляет собой маленькую точку на средней высоте (·), отсюда и произошло название «скалярный продукт». Поскольку это произведение имеет только величину, оно также известно как скалярное произведение .
A · B = AB cos θ
Скалярное произведение распределительное…
A · ( B + C ) = A · B + A · C
и коммутативный…
A · B = B · A
Поскольку проекция вектора на сам себя оставляет его величину неизменной, точечный продукт любого вектора на себя является квадратом величины этого вектора.
A · A = AA cos 0 ° = A 2
Применение этого следствия к единичным векторам означает, что скалярное произведение любого единичного вектора с самим собой равно единице. Кроме того, поскольку вектор не имеет проекции, перпендикулярной самому себе, скалярное произведение любого единичного вектора на любой другой равно нулю.
î · î = ĵ · ĵ = k̂ · k̂ = (1) (1) (cos 0 °) = 1
î · = ĵ · k̂ = k̂ · î = (1) (1) (cos 90 °) = 0
Используя эти знания, мы можем вывести формулу для скалярного произведения любых двух векторов в прямоугольной форме.Полученный продукт выглядит ужасно беспорядочно, но состоит в основном из нулевых членов.
| A · B = | ( A x î + A y ĵ + A z k̂ ) · ( B x ĵ + B z k̂ ) | |||||||||||
| A · B = | A x или | · | B x î | + | A x или | · | B y ĵ | + | A x или | · | B z k̂ | |
| + | A y ĵ | · | B x î | + | A y ĵ | · | B y ĵ | + | A y ĵ | · | B z k̂ | |
| + | A z k̂ | · | B x î | + | A z k̂ | · | B y ĵ | + | A z k̂ | · | B z k̂ | |
| A · B = | A x B x + A y B y + A z B z | |||||||||||
Скалярное произведение двух векторов, таким образом, является суммой произведений их параллельных компонентов.Отсюда мы можем вывести теорему Пифагора в трех измерениях.
A · A = AA cos 0 ° = A x A x + A y A y + A z A z
A 2 = A x 2 + A y 2 + A z 2
крестное произведение
Геометрически перекрестное произведение двух векторов — это площадь параллелограмма между ними.
Символ, используемый для представления этой операции, представляет собой большой диагональный крест (×), отсюда и произошло название «перекрестное произведение». Поскольку это произведение имеет величину и направление, оно также известно как векторное произведение .
A × B = AB sin θ n̂
Вектор n̂ (n hat) — это единичный вектор, перпендикулярный плоскости, образованной двумя векторами. Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Перекрестное произведение распределительное…
A × ( B + C ) = ( A × B ) + ( A × C )
, но не , а не , коммутативный…
A × B = — B × A
Изменение порядка перекрестного умножения меняет направление произведения на противоположное.
Поскольку два идентичных вектора образуют вырожденный параллелограмм без площади, перекрестное произведение любого вектора на себя равно нулю…
A × A = 0
Применение этого следствия к единичным векторам означает, что произведение любого единичного вектора на себя равно нулю.
î × î = ĵ × ĵ = k̂ × k̂ = (1) (1) (sin 0 °) = 0
Следует отметить, что произведение любого единичного вектора на любой другой будет иметь величину, равную единице. (В конце концов, синус 90 ° равен единице.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение , а не коммутативно, порядок операций важен.
- Держите правую руку ровно так, чтобы большой палец был перпендикулярен пальцам. Никогда не сгибайте большой палец.
- Укажите пальцами в направлении первого вектора.
- Сориентируйте ладонь так, чтобы при сгибании пальцев они указывали в направлении второго вектора.
- Ваш большой палец теперь указывает в направлении перекрестного произведения.
Правая система координат , которая является обычной системой координат, используемой в физике и математике, — это система, в которой любое циклическое произведение трех осей координат положительно, а любое антициклическое произведение отрицательно.Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр. Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно циклическим и положительным. Любой продукт, который движется в противоположном направлении, — это антициклический, и отрицательный.
| Перекрестное произведение циклической пары единичных векторов равно положительным . | Перекрестное произведение антициклической пары единичных векторов равно отрицательным . |
Используя эти знания, мы можем вывести формулу для векторного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто это будет ужасный беспорядок, и это так!
A × B = ( A x î + A y ĵ + A z k̂ ) × 9048 + B y ĵ + B z k̂ )
Произведение двух трехчленов состоит из девяти членов.
| A × B | = | A x или | × | B x î | + | A x или | × | B y ĵ | + | A x или | × | B z k̂ |
| + | A y ĵ | × | B x î | + | A y ĵ | × | B y ĵ | + | A y ĵ | × | B z k̂ | |
| + | A z k̂ | × | B x î | + | A z k̂ | × | B y ĵ | + | A z k̂ | × | B z k̂ |
Три из них равны нулю.Устраните их.
| A × B | = | A x B y k̂ | – | A x B z ĵ |
| – | A y B x k̂ | + | A y B z до | |
| + | A z B x ĵ | – | A z B y до |
Сгруппируйте термины по единичному вектору и коэффициенту.
A × B = ( A y B z — A z B y ) î
Есть более простой способ написать это. Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой является единичными векторами, вторая строка — первым вектором, а третья строка — вторым вектором.Условно…
| A × B = | – | ĵ | кО |
| A x | A y | A z | |
| B x | B y | B z |
Расширение определителя 3 × 3 его первой строкой является первым шагом.Это дает нам три определителя 2 × 2.
| A × B = | A y | A z | – — | A x | A z | ĵ + | A x | A y | кО |
| B y | B z | B x | B z | B x | B y |
Эти детерминанты 2 × 2 можно найти быстро.Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать термины и множители.
A × B = ( A y B z — A z B y ) î
Отрицательные собственные значения
Отрицательные собственные значения
следующий: Ссылки
Up: Достаточные условия для умножения
Предыдущее: Неположительные собственные значения
Следующая лемма нам понадобится при доказательстве теоремы 3.1,
в точке, где мы применим лемму 2.3.
Доказательство: Пусть,
быть векторами такими, что если и только
если, i = 1« n , и тогда и только тогда, когда
, j = 1« м . Тогда вектор находится в
тогда и только тогда, когда есть такие константы. Для этого нам понадобится
так что d находится в том и только в том случае, если вектор
находится в промежутке векторов
Данная характеристика изображения C под проекцией и
того факта, что внутренний продукт является непрерывным, достаточно для получения результата.
Теперь мы разработаем критерий, немного отличающийся от предыдущего.
раздел. Предположим, что состоит из k
отрицательные собственные значения (с учетом кратности), что ker ( A ) конечно
размерный (это будет подразумеваться тривиальным требованием), и
для некоторых
. Предположим, что это натянуто на
. Можно предположить, что,,
ортогональны ker ( A ) путем проецирования на. Определим E как
Доказательство: Нам снова нужно показать, что A сильно положителен на
.Путем ортогонализации матрицы E как в
По лемме 2.2 можно считать, что если и что. Брать
ан. Тогда x = y + z , где и. Один
легко это видит.
Рассуждая, как в теореме 2.1, можно показать, что существуют
константы,, так что, где v ортогонален,,. В
Кроме того, v ортогонален ker ( A ), поскольку y и ‘s являются.
Подставляя,
Так как у нас есть, так что
это справедливо для всех j .Следовательно
с последним неравенством, вытекающим из того, что v ортогонален
все неположительные собственные векторы A . Теперь мы должны соотнести длину с
до x . Как и раньше, воспользуемся леммой 2.3. С
тривиально, существует так, что, где не зависит от x .
Для аналогичного неравенства, относящегося к и, мы
сначала нужно показать, что ортогональная проекция на
имеет только тривиальное пересечение с промежутком
.Предположим, что некоторые
также находится в ортогональной проекции на. Там есть
вектор так что. Тогда для
каждый j от 1 до k ,
так что это нулевой вектор. Чтобы применить лемму 2.3, мы должны
также показывают, что изображение при ортогональной проекции на
закрыто. Это следует из леммы 3.1. Следовательно,
есть некоторые (не в зависимости от x или y ) так что. Теперь получаем, что
для всех, так что A сильно положит.В виде
выше, этого достаточно для получения результата.
Благодарности. Я хотел бы поблагодарить Джона Мэддокса за
предлагая расширить результаты [6]. Я бы также хотел
поблагодарить Томаса Шлумпрехта за полезный разговор, касающийся
Лемма 3.1.
следующий: Ссылки
Up: Достаточные условия для умножения
Предыдущее: Неположительные собственные значения
Вт 20 августа 10:23:22 CDT 1996
.

