15 удивительных, интересных и невероятных парадоксов!
Слову парадокс мы обязаны древним грекам — изобретателям демократии и логики. Парадокс с древнегреческого переводится как “странный” и “неожиданный”. Парадокс существует в реальности, но по логике не должен.
Какие же парадоксы существуют?
1.Парадокс Пиноккио
Помните героя мультфильма, который лгал и из-за этого у него вырастал нос? В философии больше известен как парадокс лжеца. То есть если человек врет, но говорит правду: “Я сейчас вру” — является одновременно правдой и ложью.
Пиноккио говорит: “Мой нос сейчас растёт” — и это означает, если он говорит правду, то нос должен расти, и эта же фраза обозначает ложь, но ее быть не может, так как правду мы уже выяснили.
2. Проблема курицы и яйца
Что было раньше: курица или яйцо? Изучавшие зоологию знают ответ: птицы появились задолго до куриц и яйцо появилось раньше. Но что появилось ранее животное, которое отложило яйцо или яйцо из которого вылупилось животное? Загвоздка парадокса в том, что причинно-следственную связь можно выявить только учитывая явления нечеткого объема. В ходе эволюции животные сменили несколько способов выведения потомства. И достоверно узнать, что же было раньше пока не представляется возможным.
3. Парадокс всемогущества
Если представить, что существует всемогущее существо, для которого нет невыполнимых действий, может ли оно ограничить себя и если ограничит останется ли оно всемогущим?
Может ли это существо создать камень, который не способно поднять? Если может то, то тогда оно не поднимает камень, а значит оно не всемогуще. А если не может создать — то где же его способности?
Определение всемогущества подразумевает собой отсутствие ограничений, но наличие ограничений (например, неспособность поднять камень) не попадает в категорию всемогущества.
4. Парадокс дедушки
Этот парадокс понравится любителям помечтать о путешествиях во времени.
Предположим, что вы можете вернуться в прошлое и убить своего дедушку. Хорошо, если это слишком жестоко, вам просто надо отлучить дедушку от брака с бабушкой и тогда не появится на свет один из ваших родителей.
А если ваши родители не появятся на свет, то ваша мама не сможет родить вас. И вы не сможете попасть в прошлое и расстроить свадьбу своих дедушки и бабушки. Таким образом, вы не сможете помешать им и появитесь на свет.
Ученые на этот счет разделились во мнении: часть считает, что это доказательство невозможности путешествий по времени, другая часть считает, что убивая дедушку в прошлом вы просто создаете еще одну реальность, где вас не существует.
5. Парадокс летящей стрелы
Представьте себе движение стрелы. Чтобы стрела двигалась она должна изменить свою позицию. В любой момент летящая стрела остается неподвижной. Еще в 6 веке Зенон говорил об отсутствии движения, основываясь на том, что движущееся тело должно дойти до половины прежде чем завершит движение. Но если оно в каждый момент времени неподвижно, оно не дойдет до половины.
6. Парадокс Сорита.
Если взять кучу песка и убирать оттуда песчинки. И десять миллионов песчинок — это куча песка, но куча минус одна песчинка это все еще куча песка. Куча будет оставаться кучей песка, пока не оставить там только одну песчинку. Можно также утверждать, что куча из 10 тысяч песчинок уже не куча песка, но если ее увеличить на одну песчинку, то она станет кучей. Любой ответ должен прямо отрицать такое понятие, как куча.
7. Парадокс Ольберса
Мало кто про него слышал, в астрофизике парадокс Ольберса это утверждение о том, что темнота ночного неба опровергает предположение о бесконечности Вселенной. В темном парадоксе ночного неба утверждается, что под любым углом наблюдения с Земли линия видимости закончится достигнув земли. Представьте себе человека в лесу с одними белыми деревьями. Если он смотрит вверх и по сторонам леса он же не будет видеть только белый цвет? Это и заставляет задуматься нас о том, почему мы не видим только свет звезд в ночном небе.
8. Ахиллес и черепаха
Это одна из апорий Зенона, парадоксом она не является, но тем не менее интересна. Если Ахиллес и черепаха решат бежать наперегонки, но Ахиллес даст форму черепахе в 30 метров, то как скоро Ахиллес догонит черепаху?
Ахиллес бежит быстрее черепахи, но черепаха тоже двигается, хоть и медленно. Представим, что Ахиллес за какое-то время добежит до точки, где стартовала черепаха. Черепаха продвинулась за это время на пару метров. Ахиллесу понадобится время чтобы добежать эти пару метров. Но черепаха также не останется на месте. И также будет с третьей и последующими точками. То есть черепаха будет всегда впереди Ахиллеса. Проблема данной апории в том, что мы используем математическую логику, там где она неприменима.
9. Корабль Тесея
Тесей — один из героев греческих мифов, царь афинян. По легенде, когда Тесей вернулся с острова Крит в Афины горожане в знак почтения несколько сотен лет хранили корабль Тесея. Судно постепенно старело и в нем заменялись доски, а потом и мачты и спустя некоторое время оно уже не содержало в себе ни одного куска старых досок. Одним из любимых вопросов философов вроде Гоббса и Джона Локка был вопрос: можно ли считать этот корабль, тем кораблем, на котором вернулся Тесей. Будет ли объект тем же самым, если заменить в нем все детали? Разные философские школы давали разный ответ на этот вопрос.
10. Парадокс буриданового осла
Голодный осел оказавшись между двумя стогами сена на равном расстоянии от каждого не сможет решить с какого стога сена начать и умрет от голода. Это описание нерешительности человека в рациональных решениях. Этот парадокс назван в честь французского философа Жана Буридана, но известен этот парадокс еще со времен Аристотеля. Аристотель рассуждал о человеке, который испытывал одновременно жажду и голод и не мог решить начать ему есть или пить и в итоге не смог сделать выбор. Жан Буридан в своих трудах рассуждал о моральном детерминизме. В нем утверждалось то, что человек находясь в ситуации выбора должен выбирать большее добро. Критики философа начали приводить в пример осла, который так и не решился выбрать между одинаковыми по размеру стогами сена и умершего от голода осла. Так этот парадокс и закрепился за фамилией французского философа.
11. Дилемма крокодила
Этот парадокс чем-то похож на парадокс лжеца. Авторство данного парадокса приписывают Кораксу — знаменитому софисту. Представьте, что крокодил отнял ребенка у матери, и предлагает ей ответить на вопрос вернет ли он ей ребенка или нет. Если мама отвечает правильно, то ребенок возвращается ей, если нет то крокодил не вернет ребенка.
Парадокс возникнет если мама ребенка ответит: “Нет, ты не вернешь ребенка”.
То есть если крокодил вернет ребенка, то мать не угадала, и ребенка нужно оставить крокодилу. Но если крокодил решит не возвращать ребенка, то получается, что мать была права и ребенка надо вернуть. То есть крокодил не может вернуть ребенка и не может оставить его себе.
12. Парадокс неожиданной казни.
Осужденного приговорили к смертной казни через повешение. Судья также упомянул, что казнь состоится в любой будний день в полдень на следующей неделе и часть наказания в том, что ему не скажут точную дату. Он узнает, что его ведут на виселицу, когда зайдет палач.
В камере преступник решает, что смерти можно избежать.
Он начинает думать, что в пятницу его не могут повесить, потому что это не станет неожиданностью. Поэтому он исключает пятницу, и если его не повесят в среду, то и четверг не станет неожиданностью. И так он исключил все дни недели. Пока к нему в среду не пришел палач в один из дней и не повел его на казнь.
13. Парадокс парикмахера
В одном городе есть всего один мужской парикмахер и все мужчины этого города бреются налысо. Часть бреются сами, часть ходит к парикмахеру. Нам кажется, что работает именно это правило. Получается, что парикмахер бреет себя сам. Но если парикмахер не бреет себя сам, то по правилу он должен брить себя. И это же работает в обратную сторону: если он бреет себя сам, он не должен брить себя сам.
14. Парадокс мэров
Представьте себе, что в вымышленной стране придумали закон, согласно которому все мэры должны жить вне своих городов, а именно в специальном городе для мэров. Тогда где будет жить мэр города мэров?
15. Парадокс непреодолимой силы
Сформулирован он следующим образом, если непреодолимая сила встречает непреодолимый объект, что происходит? Например, если пуля, пробивающая все на свете, встречает на своем пути непробиваемый бронежилет? Однако современная наука не считает, что есть непреодолимая сила и не существует полностью объектом, которые не могут быть сдвинуты. Непреодолимой силе нужна бесконечная энергия, а ее не существует или пока не обнаружили.
Самые известные парадоксы в теории вероятностей

Проблема Монти Холла
Именно эту задачу в фильме «Двадцать одно» предложил студентам хитрый профессор MIT. Дав верный ответ, главный герой попадает в команду блестящих молодых математиков, обыгрывающих казино в Лас-Вегасе.
Классическая формулировка звучит так: «Допустим, некоему игроку предложили поучаствовать в известном американском телешоу Let’s Make a Deal, которое ведет Монти Холл, и ему необходимо выбрать одну из трех дверей. За двумя дверьми находятся козы, за одной — главный приз, автомобиль, ведущий знает расположение призов. После того, как игрок делает свой выбор, ведущий открывает одну из оставшихся дверей, за которой находится коза, и предлагает игроку изменить свое решение. Стоит ли игроку согласиться или лучше сохранить свой первоначальный выбор?»
Вот типичный ход рассуждений: после того, как ведущий открыл одну из дверей и показал козу, игроку остается выбрать между двумя дверями. Машина находится за одной из них, значит, вероятность ее угадать составляет ½. Так что нет разницы — менять свой выбор или нет. И тем не менее, теория вероятностей гласит, что можно увеличить свои шансы на выигрыш, изменив решение. Разберемся, почему это так.
Для этого вернемся на шаг назад. В тот момент, когда мы сделали свой изначальный выбор, мы разделили двери на две части: выбранная нами и две остальные. Очевидно, что вероятность того, что автомобиль прячется за «нашей» дверью, составляет ⅓ — соответственно, автомобиль находится за одной из двух оставшихся дверей с вероятностью ⅔. Когда ведущий показывает, что за одной из этих дверей — коза, получается, что эти ⅔ шанса приходятся на вторую дверь. А это сводит выбор игрока к двум дверям, за одной из которых (изначально выбранной) автомобиль находится с вероятностью ⅓, а за другой — с вероятностью ⅔. Выбор становится очевидным. Что, разумеется, не отменяет того факта, что с самого начала игрок мог выбрать дверь с автомобилем.
Задача трех узников
Парадокс трех узников схож с проблемой Монти Холла, хотя действие разворачивается в более драматических условиях. Трое заключенных (А, Б и В) приговорены к смертной казни и помещены в одиночные камеры. Губернатор случайным образом выбирает одного из них и дает ему помилование. Надзиратель знает, кто из троих помилован, но ему велено держать это в тайне. Узник A просит стражника сказать ему имя второго заключенного (кроме него самого), который точно будет казнен: «если Б помилован, скажи мне, что казнен будет В. Если помилован В, скажи мне, что казнен будет Б. Если они оба будут казнены, а помилован я, подбрось монету, и скажи любое из этих двух имен». Надзиратель говорит, что будет казнен узник Б. Стоит ли радоваться узнику А?
Казалось бы, да. Ведь до получения этой информации вероятность смерти узника А составляла ⅔, а теперь он знает, что один из двух других узников будет казнен — значит, вероятность его казни снизилась до ½. Но на самом деле узник А не узнал ничего нового: если помилован не он, ему назовут имя другого узника, а он и так знал, что кого-то из двоих оставшихся казнят. Если же ему повезло, и казнь отменили, он услышит случайное имя Б или В. Поэтому его шансы на спасение никак не изменились.
А теперь представим, что кто-то из оставшихся узников узнает о вопросе узника А и полученном ответе. Это изменит его представления о вероятности помилования.
Если разговор подслушал узник Б, он узнает, что его точно казнят. А если узник В, то вероятность его помилования будет составлять ⅔. Почему так произошло? Узник А не получил никакой информации, и его шансы на помилование по-прежнему ⅓. Узник Б точно не будет помилован, и его шансы равны нулю. Значит, вероятность того, что на свободу выйдет третий узник, равна ⅔.

Парадокс двух конвертов
Этот парадокс стал известен благодаря математику Мартину Гарднеру, и формулируется следующим образом: «Предположим, вам с другом предложили два конверта, в одном из которых лежит некая сумма денег X, а в другом — сумма вдвое больше. Вы независимо друг от друга вскрываете конверты, пересчитываете деньги, после чего можете обменяться ими. Конверты одинаковые, поэтому вероятность того, что вам достанется конверт с меньшей суммой, составляет ½. Допустим, вы открыли конверт и обнаружили в нем $10.
Следовательно, в конверте вашего друга может быть равновероятно $5 или $20. Если вы решаетесь на обмен, то можно подсчитать математическое ожидание итоговой суммы — то есть, ее среднее значение. Она составляет 1/2х$5+1/2×20=$12,5. Таким образом, обмен вам выгоден. И, скорее всего, ваш друг будет рассуждать точно так же. Но очевидно, что обмен не может быть выгоден вам обоим. В чем же ошибка?»
Парадокс заключается в том, что пока вы не вскрыли свой конверт, вероятности ведут себя добропорядочно: у вас действительно 50-процентный шанс обнаружить в своем конверте сумму X и 50-процентный — сумму 2X. И здравый смысл подсказывает, что информация об имеющейся у вас сумме не может повлиять на содержимое второго конверта.
Тем не менее, как только вы вскрываете конверт, ситуация кардинально меняется (этот парадокс чем-то похож на историю с котом Шредингера, где само наличие наблюдателя влияет на положение дел). Дело в том, что для соблюдения условий парадокса вероятность нахождения во втором конверте большей или меньшей суммы, чем у вас, должна быть одинаковой. Но тогда равновероятно любое значение этой суммы от нуля до бесконечности. А если равновероятно бесконечное число возможностей, в сумме они дают бесконечность. А это невозможно.
Для наглядности можно представить, что вы обнаруживаете в своем конверте один цент. Очевидно, что во втором конверте не может быть суммы вдвое меньше.
Любопытно, что дискуссии относительно разрешения парадокса продолжаются и в настоящее время. При этом предпринимаются попытки как объяснить парадокс изнутри, так и выработать наилучшую стратегию поведения в подобной ситуации. В частности, профессор Томас Кавер предложил оригинальный подход к формированию стратегии — менять или не менять конверт, руководствуясь неким интуитивным ожиданием. Скажем, если вы открыли конверт и обнаружили в нем $10 — небольшую сумму по вашим прикидкам — стоит его обменять. А если в конверте, скажем, $1 000, что превосходит ваши самые смелые ожидания, то меняться не надо. Эта интуитивная стратегия в случае, если вам регулярно предлагают выбирать два конверта, дает возможность увеличить суммарный выигрыш больше, чем стратегия постоянной смены конвертов.

Парадокс мальчика и девочки
Этот парадокс был также предложен Мартином Гарднером и формулируется так: «У мистера Смита двое детей. Хотя бы один ребенок — мальчик. Какова вероятность того, что и второй — тоже мальчик?»
Казалось бы, задача проста. Однако если начать разбираться, обнаруживается любопытное обстоятельство: правильный ответ будет отличаться в зависимости от того, каким образом мы будем подсчитывать вероятность пола другого ребенка.
Вариант 1
Рассмотрим все возможные комбинации в семьях с двумя детьми:
— Девочка/Девочка
— Девочка/Мальчик
— Мальчик/Девочка
— Мальчик/Мальчик
Вариант девочка/девочка нам не подходит по условиям задачи. Поэтому для семьи мистера Смита возможны три равновероятных варианта — а значит, вероятность того, что другой ребенок тоже окажется мальчиком, составляет ⅓. Именно такой ответ и давал сам Гарднер первоначально.
Вариант 2
Представим, что мы встречаем мистера Смита на улице, когда он гуляет с сыном. Какова вероятность того, что второй ребенок — тоже мальчик? Поскольку пол второго ребенка никак не зависит от пола первого, очевидным (и правильным) ответом является ½.
Почему так происходит, ведь, казалось бы, ничего не изменилось?
Все зависит от того, как мы подходим к вопросу подсчета вероятности. В первом случае мы рассматривали все возможные варианты семьи Смита. Во втором — мы рассматривали все семьи, подпадающие под обязательное условие «должен быть один мальчик». Расчет вероятности пола второго ребенка велся с этим условием (в теории вероятностей это называется «условная вероятность»), что и привело к результату, отличному от первого.
Фото: Morini & Montanari.
Источник: T&P.
Топ-10 парадоксов современности (9 фото + видео) » Триникси
В этом посте довольно детальны описаны самые странные и необычные парадоксы нашего времени, которые до сих пор не были окончательно изучены наукой. Довольно интересная статья, которая расширит ваш кругозор.
1. Парадокс Банаха-Тарского

Представьте себе, что вы держите в руках шар. А теперь представьте, что вы начали рвать этот шар на куски, причём куски могут быть любой формы, какая вам нравится. После сложите кусочки вместе таким образом, чтобы у вас получилось два шара вместо одного. Каков будет размер этих шаров по сравнению с шаром-оригиналом?
Согласно теории множеств, два получившихся шара будут такого же размера и формы, как шар-оригинал. Кроме того, если учесть, что шары при этом имеют разный объём, то любой из шаров может быть преобразован в соответствии с другим. Это позволяет сделать вывод, что горошину можно разделить на шары размером с Солнце.
Хитрость парадокса заключается в том, что вы можете разорвать шары на куски любой формы. На практике сделать это невозможно — структура материала и в конечном итоге размер атомов накладывают некоторые ограничения.
Для того чтобы было действительно возможно разорвать шар так, как вам нравится, он должен содержать бесконечное число доступных нульмерных точек. Тогда шар из таких точек будет бесконечно плотным, и когда вы разорвёте его, формы кусков могут получиться настолько сложными, что не будут иметь определенного объёма. И вы можете собрать эти куски, каждый из которых содержит бесконечное число точек, в новый шар любого размера. Новый шар будет по-прежнему состоять из бесконечных точек, и оба шара будут одинаково бесконечно плотными.
Если вы попробуете воплотить идею на практике, то ничего не получится. Зато всё замечательно получается при работе с математическими сферами — безгранично делимыми числовыми множествами в трехмерном пространстве. Решённый парадокс называется теоремой Банаха-Тарского и играет огромную роль в математической теории множеств.
2. Парадокс Пето
Очевидно, что киты гораздо крупнее нас, это означает, что у них в телах гораздо больше клеток. А каждая клетка в организме теоретически может стать злокачественной. Следовательно, у китов гораздо больше шансов заболеть раком, чем у людей, так?
Не так. Парадокс Пето, названный в честь оксфордского профессора Ричарда Пето, утверждает, что корреляции между размером животного и раком не существует. У людей и китов шанс заболеть раком примерно одинаков, а вот некоторые породы крошечных мышей имеют гораздо больше шансов.
Некоторые биологи полагают, что отсутствие корреляции в парадоксе Пето можно объяснить тем, что более крупные животные лучше сопротивляются опухоли: механизм работает таким образом, чтобы предотвратить мутацию клеток в процессе деления.
3. Проблема настоящего времени

Чтобы что-то могло физически существовать, оно должно присутствовать в нашем мире в течение какого-то времени. Не может быть объекта без длины, ширины и высоты, а также не может быть объекта без «продолжительности» — «мгновенный» объект, то есть тот, который не существует хотя бы какого-то количества времени, не существует вообще.
Согласно универсальному нигилизму, прошлое и будущее не занимают времени в настоящем. Кроме того, невозможно количественно определить длительность, которую мы называем «настоящим временем»: любое количество времени, которое вы назовёте «настоящим временем», можно разделить на части — прошлое, настоящее и будущее.
Если настоящее длится, допустим, секунду, то эту секунду можно разделить на три части: первая часть будет прошлым, вторая — настоящим, третья — будущим. Треть секунды, которую мы теперь называем настоящим, можно тоже разделить на три части. Наверняка идею вы уже поняли — так можно продолжать бесконечно.
Таким образом, настоящего на самом деле не существует, потому что оно не продолжается во времени. Универсальный нигилизм использует этот аргумент, чтобы доказать, что не существует вообще ничего.
4. Парадокс Моравека
 При решении проблем, требующих вдумчивого рассуждения, у людей случаются затруднения. С другой стороны, основные моторные и сенсорные функции вроде ходьбы не вызывают никаких затруднений вообще.
При решении проблем, требующих вдумчивого рассуждения, у людей случаются затруднения. С другой стороны, основные моторные и сенсорные функции вроде ходьбы не вызывают никаких затруднений вообще.
Но если говорить о компьютерах, всё наоборот: компьютерам очень легко решать сложнейшие логические задачи вроде разработки шахматной стратегии, но куда сложнее запрограммировать компьютер так, чтобы он смог ходить или воспроизводить человеческую речь. Это различие между естественным и искусственным интеллектом известно как парадокс Моравека.
Ханс Моравек, научный сотрудник факультета робототехники Университета Карнеги-Меллона, объясняет это наблюдение через идею реверсного инжиниринга нашего собственного мозга. Реверсный инжиниринг труднее всего провести при задачах, которые люди выполняют бессознательно, например, двигательных функциях.
Поскольку абстрактное мышление стало частью человеческого поведения меньше 100 000 лет назад, наша способность решать абстрактные задачи является сознательной. Таким образом, для нас намного легче создать технологию, которая эмулирует такое поведение. С другой стороны, такие действия, как ходьба или разговор, мы не осмысливаем, так что заставить искусственный интеллект делать то же самое нам сложнее.
5. Закон Бенфорда
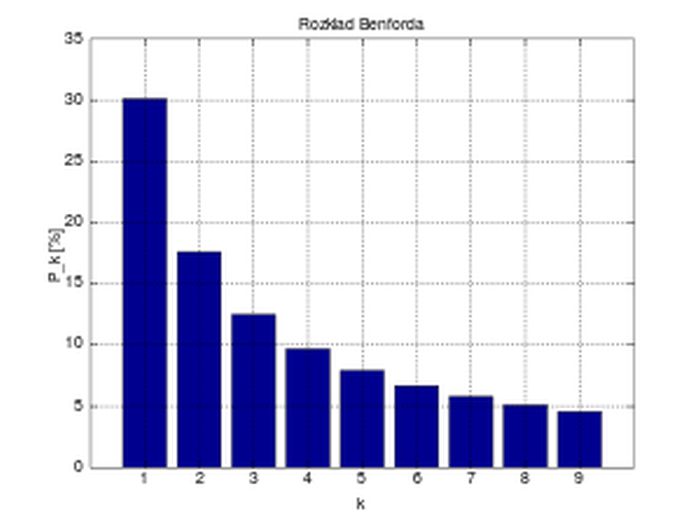
Каков шанс, что случайное число начнётся с цифры «1»? Или с цифры «3»? Или с «7»? Если вы немного знакомы с теорией вероятности, то можете предположить, что вероятность — один к девяти, или около 11%.
Если же вы посмотрите на реальные цифры, то заметите, что «9» встречается гораздо реже, чем в 11% случаев. Также куда меньше цифр, чем ожидалось, начинается с «8», зато колоссальные 30% чисел начинаются с цифры «1». Эта парадоксальная картина проявляется во всевозможных реальных случаях, от количества населения до цен на акции и длины рек.
Физик Фрэнк Бенфорд впервые отметил это явление в 1938-м году. Он обнаружил, что частота появления цифры в качестве первой падает по мере того, как цифра увеличивается от одного до девяти. То есть «1» появляется в качестве первой цифры примерно в 30,1% случаев, «2» появляется около 17,6% случаев, «3» — примерно в 12,5%, и так далее до «9», выступающей в качестве первой цифры всего лишь в 4,6% случаев.
Чтобы понять это, представьте себе, что вы последовательно нумеруете лотерейные билеты. Когда вы пронумеровали билеты от одного до девяти, шанс любой цифры стать первой составляет 11,1%. Когда вы добавляете билет № 10, шанс случайного числа начаться с «1» возрастает до 18,2%. Вы добавляете билеты с № 11 по № 19, и шанс того, что номер билета начнётся с «1», продолжает расти, достигая максимума в 58%. Теперь вы добавляете билет № 20 и продолжаете нумеровать билеты. Шанс того, что число начнётся с «2», растёт, а вероятность того, что оно начнётся с «1», медленно падает.
Закон Бенфорда не распространяется на все случаи распределения чисел. Например, наборы чисел, диапазон которых ограничен (человеческий рост или вес), под закон не попадают. Он также не работает с множествами, которые имеют только один или два порядка.
Тем не менее, закон распространяется на многие типы данных. В результате власти могут использовать закон для выявления фактов мошенничества: когда предоставленная информация не следует закону Бенфорда, власти могут сделать вывод, что кто-то сфабриковал данные.
6. C-парадокс

Гены содержат всю информацию, необходимую для создания и выживания организма. Само собой разумеется, что сложные организмы должны иметь самые сложные геномы, но это не соответствует истине.
Одноклеточные амёбы имеют геномы в 100 раз больше, чем у человека, на самом деле, у них едва ли не самые большие из известных геномов. А у очень похожих между собой видов геном может кардинально различаться. Эта странность известна как С-парадокс.
Интересный вывод из С-парадокса — геном может быть больше, чем это необходимо. Если все геномы в человеческой ДНК будут использоваться, то количество мутаций на поколение будет невероятно высоким.
Геномы многих сложных животных вроде людей и приматов включают в себя ДНК, которая ничего не кодирует. Это огромное количество неиспользованных ДНК, значительно варьирующееся от существа к существу, кажется, ни от чего не зависит, что и создаёт C-парадокс.
7. Бессмертный муравей на верёвке

Представьте себе муравья, ползущего по резиновой верёвке длиной один метр со скоростью один сантиметр в секунду. Также представьте, что верёвка каждую секунду растягивается на один километр. Дойдёт ли муравей когда-нибудь до конца?
Логичным кажется то, что нормальный муравей на такое не способен, потому что скорость его движения намного ниже скорости, с которой растягивается верёвка. Тем не менее, в конечном итоге муравей доберётся до противоположного конца.
Когда муравей ещё даже не начал движение, перед ним лежит 100% верёвки. Через секунду верёвка стала значительно больше, но муравей тоже прошёл некоторое расстояние, и если считать в процентах, то расстояние, которое он должен пройти, уменьшилось — оно уже меньше 100%, пусть и ненамного.
Хотя верёвка постоянно растягивается, маленькое расстояние, пройденное муравьём, тоже становится больше. И, хотя в целом верёвка удлиняется с постоянной скоростью, путь муравья каждую секунду становится немного меньше. Муравей тоже всё время продолжает двигаться вперёд с постоянной скоростью. Таким образом, с каждой секундой расстояние, которое он уже прошёл, увеличивается, а то, которое он должен пройти — уменьшается. В процентах, само собой.
Существует одно условие, чтобы задача могла иметь решение: муравей должен быть бессмертным. Итак, муравей дойдёт до конца через 2,8×1043.429 секунд, что несколько дольше, чем существует Вселенная.
8. Парадокс экологического баланса

Модель «хищник-жертва» — это уравнение, описывающее реальную экологическую обстановку. Например, модель может определить, насколько изменится численность лис и кроликов в лесу. Допустим, что травы, которой питаются кролики, в лесу становится всё больше. Можно предположить, что для кроликов такой исход благоприятен, потому что при обилии травы они будут хорошо размножаться и увеличивать численность.
Парадокс экологического баланса утверждает, что это не так: сначала численность кроликов действительно возрастёт, но рост популяции кроликов в закрытой среде (лесу) приведёт к росту популяции лисиц. Затем численность хищников увеличится настолько, что они уничтожат сначала всю добычу, а потом вымрут сами.
На практике этот парадокс не действует на большинство видов животных — хотя бы потому, что они не живут в закрытой среде, поэтому популяции животных стабильны. Кроме того, животные способны эволюционировать: например, в новых условиях у добычи появятся новые защитные механизмы.
9. Парадокс тритона
Соберите группу друзей и посмотрите все вместе это видео. Когда закончите, пусть каждый выскажет своё мнение, увеличивается звук или уменьшается во время всех четырёх тонов. Вы удивитесь, насколько разными будут ответы.
Чтобы понять этот парадокс, вам нужно знать кое-что о музыкальных нотах. У каждой ноты есть определённая высота, от которой зависит, высокий или низкий звук мы слышим. Нота следующей, более высокой октавы, звучит в два раза выше, чем нота предыдущей октавы. А каждую октаву можно разделить на два равных тритонных интервала.
На видео тритон разделяет каждую пару звуков. В каждой паре один звук представляет собой смесь одинаковых нот из разных октав — например, сочетание двух нот до, где одна звучит выше другой. Когда звук в тритоне переходит с одной ноты на другую (например, соль-диез между двумя до), можно совершенно обоснованно интерпретировать ноту как более высокую или более низкую, чем предыдущая.
Другое парадоксальное свойство тритонов — это ощущение, что звук постоянно становится ниже, хотя высота звука не меняется.
10. Эффект Мпембы

Перед вами два стакана воды, совершенно одинаковые во всём, кроме одного: температура воды в левом стакане выше, чем в правом. Поместите оба стакана в морозилку. В каком стакане вода замёрзнет быстрее? Можно решить, что в правом, в котором вода изначально была холоднее, однако горячая вода замёрзнет быстрее, чем вода комнатной температуры.
Этот странный эффект назван в честь студента из Танзании, который наблюдал его в 1986-м году, когда замораживал молоко, чтобы сделать мороженое. Некоторые из величайших мыслителей — Аристотель, Фрэнсис Бэкон и Рене Декарт — и ранее отмечали это явление, но не были в состоянии объяснить его. Аристотель, например, выдвигал гипотезу, что какое-либо качество усиливается в среде, противоположной этому качеству.
Эффект Мпембы возможен благодаря нескольким факторам. Воды в стакане с горячей водой может быть меньше, так как часть её испарится, и в результате замёрзнуть должно меньшее количество воды. Также горячая вода содержит меньше газа, а значит, в такой воде легче возникнут конвекционные потоки, следовательно, замерзать ей будет проще.
Другая теория строится на том, что ослабевают химические связи, удерживающие молекулы воды вместе. Молекула воды состоит из двух атомов водорода, связанных с одним атомом кислорода. Когда вода нагревается, молекулы немного отодвигаются друг от друга, связь между ними ослабевает, и молекулы теряют немного энергии — это позволяет горячей воде остывать быстрее, чем холодной.
Отсюда
Самые известные парадоксы в теории вероятностей

«Существуют три вида лжи: ложь, наглая ложь и статистика». Эта фраза, приписанная Марком Твеном премьер-министру Великобритании Бенджамину Дизраэли, неплохо отражает отношение большинства к математическим закономерностям. Действительно, теория вероятностей порой подкидывает удивительные факты, в которые сложно поверить с первого взгляда — и которые, тем не менее, подтверждены наукой. Вспоминаем самые известные парадоксы.

Проблема Монти Холла
Именно эту задачу в фильме «Двадцать одно» предложил студентам хитрый профессор MIT. Дав верный ответ, главный герой попадает в команду блестящих молодых математиков, обыгрывающих казино в Лас-Вегасе.
Классическая формулировка звучит так: «Допустим, некоему игроку предложили поучаствовать в известном американском телешоу Let’s Make a Deal, которое ведет Монти Холл, и ему необходимо выбрать одну из трех дверей. За двумя дверьми находятся козы, за одной — главный приз, автомобиль, ведущий знает расположение призов. После того, как игрок делает свой выбор, ведущий открывает одну из оставшихся дверей, за которой находится коза, и предлагает игроку изменить свое решение. Стоит ли игроку согласиться или лучше сохранить свой первоначальный выбор?»
Вот типичный ход рассуждений: после того, как ведущий открыл одну из дверей и показал козу, игроку остается выбрать между двумя дверями. Машина находится за одной из них, значит, вероятность ее угадать составляет ½. Так что нет разницы — менять свой выбор или нет. И тем не менее, теория вероятностей гласит, что можно увеличить свои шансы на выигрыш, изменив решение. Разберемся, почему это так.
Для этого вернемся на шаг назад. В тот момент, когда мы сделали свой изначальный выбор, мы разделили двери на две части: выбранная нами и две остальные. Очевидно, что вероятность того, что автомобиль прячется за «нашей» дверью, составляет ⅓ — соответственно, автомобиль находится за одной из двух оставшихся дверей с вероятностью ⅔. Когда ведущий показывает, что за одной из этих дверей — коза, получается, что эти ⅔ шанса приходятся на вторую дверь. А это сводит выбор игрока к двум дверям, за одной из которых (изначально выбранной) автомобиль находится с вероятностью ⅓, а за другой — с вероятностью ⅔. Выбор становится очевидным. Что, разумеется, не отменяет того факта, что с самого начала игрок мог выбрать дверь с автомобилем.

Задача трех узников
Парадокс трех узников схож с проблемой Монти Холла, хотя действие разворачивается в более драматических условиях. Трое заключенных (А, Б и В) приговорены к смертной казни и помещены в одиночные камеры. Губернатор случайным образом выбирает одного из них и дает ему помилование. Надзиратель знает, кто из троих помилован, но ему велено держать это в тайне. Узник A просит стражника сказать ему имя второго заключенного (кроме него самого), который точно будет казнен: «если Б помилован, скажи мне, что казнен будет В. Если помилован В, скажи мне, что казнен будет Б. Если они оба будут казнены, а помилован я, подбрось монету, и скажи любое из этих двух имен». Надзиратель говорит, что будет казнен узник Б. Стоит ли радоваться узнику А?
Казалось бы, да. Ведь до получения этой информации вероятность смерти узника А составляла ⅔, а теперь он знает, что один из двух других узников будет казнен — значит, вероятность его казни снизилась до ½. Но на самом деле узник А не узнал ничего нового: если помилован не он, ему назовут имя другого узника, а он и так знал, что кого-то из двоих оставшихся казнят. Если же ему повезло, и казнь отменили, он услышит случайное имя Б или В. Поэтому его шансы на спасение никак не изменились.
А теперь представим, что кто-то из оставшихся узников узнает о вопросе узника А и полученном ответе. Это изменит его представления о вероятности помилования.
Если разговор подслушал узник Б, он узнает, что его точно казнят. А если узник В, то вероятность его помилования будет составлять ⅔. Почему так произошло? Узник А не получил никакой информации, и его шансы на помилование по-прежнему ⅓. Узник Б точно не будет помилован, и его шансы равны нулю. Значит, вероятность того, что на свободу выйдет третий узник, равна ⅔.

Парадокс двух конвертов
Этот парадокс стал известен благодаря математику Мартину Гарднеру, и формулируется следующим образом: «Предположим, вам с другом предложили два конверта, в одном из которых лежит некая сумма денег X, а в другом — сумма вдвое больше. Вы независимо друг от друга вскрываете конверты, пересчитываете деньги, после чего можете обменяться ими. Конверты одинаковые, поэтому вероятность того, что вам достанется конверт с меньшей суммой, составляет ½. Допустим, вы открыли конверт и обнаружили в нем $10.
Следовательно, в конверте вашего друга может быть равновероятно $5 или $20. Если вы решаетесь на обмен, то можно подсчитать математическое ожидание итоговой суммы — то есть, ее среднее значение. Она составляет 1/2х$5+1/2×20=$12,5. Таким образом, обмен вам выгоден. И, скорее всего, ваш друг будет рассуждать точно так же. Но очевидно, что обмен не может быть выгоден вам обоим. В чем же ошибка?»
Парадокс заключается в том, что пока вы не вскрыли свой конверт, вероятности ведут себя добропорядочно: у вас действительно 50-процентный шанс обнаружить в своем конверте сумму X и 50-процентный — сумму 2X. И здравый смысл подсказывает, что информация об имеющейся у вас сумме не может повлиять на содержимое второго конверта.
Тем не менее, как только вы вскрываете конверт, ситуация кардинально меняется (этот парадокс чем-то похож на историю с котом Шредингера, где само наличие наблюдателя влияет на положение дел). Дело в том, что для соблюдения условий парадокса вероятность нахождения во втором конверте большей или меньшей суммы, чем у вас, должна быть одинаковой. Но тогда равновероятно любое значение этой суммы от нуля до бесконечности. А если равновероятно бесконечное число возможностей, в сумме они дают бесконечность. А это невозможно.
Для наглядности можно представить, что вы обнаруживаете в своем конверте один цент. Очевидно, что во втором конверте не может быть суммы вдвое меньше.
Любопытно, что дискуссии относительно разрешения парадокса продолжаются и в настоящее время. При этом предпринимаются попытки как объяснить парадокс изнутри, так и выработать наилучшую стратегию поведения в подобной ситуации. В частности, профессор Томас Кавер предложил оригинальный подход к формированию стратегии — менять или не менять конверт, руководствуясь неким интуитивным ожиданием. Скажем, если вы открыли конверт и обнаружили в нем $10 — небольшую сумму по вашим прикидкам — стоит его обменять. А если в конверте, скажем, $1 000, что превосходит ваши самые смелые ожидания, то меняться не надо. Эта интуитивная стратегия в случае, если вам регулярно предлагают выбирать два конверта, дает возможность увеличить суммарный выигрыш больше, чем стратегия постоянной смены конвертов.

Парадокс мальчика и девочки
Этот парадокс был также предложен Мартином Гарднером и формулируется так: «У мистера Смита двое детей. Хотя бы один ребенок — мальчик. Какова вероятность того, что и второй — тоже мальчик?»
Казалось бы, задача проста. Однако если начать разбираться, обнаруживается любопытное обстоятельство: правильный ответ будет отличаться в зависимости от того, каким образом мы будем подсчитывать вероятность пола другого ребенка.
Вариант 1
Рассмотрим все возможные комбинации в семьях с двумя детьми:
— Девочка/Девочка
— Девочка/Мальчик
— Мальчик/Девочка
— Мальчик/Мальчик
Вариант девочка/девочка нам не подходит по условиям задачи. Поэтому для семьи мистера Смита возможны три равновероятных варианта — а значит, вероятность того, что другой ребенок тоже окажется мальчиком, составляет ⅓. Именно такой ответ и давал сам Гарднер первоначально.
Вариант 2
Представим, что мы встречаем мистера Смита на улице, когда он гуляет с сыном. Какова вероятность того, что второй ребенок — тоже мальчик? Поскольку пол второго ребенка никак не зависит от пола первого, очевидным (и правильным) ответом является ½.
Почему так происходит, ведь, казалось бы, ничего не изменилось?
Все зависит от того, как мы подходим к вопросу подсчета вероятности. В первом случае мы рассматривали все возможные варианты семьи Смита. Во втором — мы рассматривали все семьи, подпадающие под обязательное условие «должен быть один мальчик». Расчет вероятности пола второго ребенка велся с этим условием (в теории вероятностей это называется «условная вероятность»), что и привело к результату, отличному от первого.
источник
Если вам понравился пост, пожалуйста, поделитесь ими со своими друзьями! 🙂
12 самых знаменитых парадоксов
Парадоксы существовали со времен древних греков. При помощи логики можно быстро найти фатальный недостаток в парадоксе, который и показывает, почему, казалось бы, невозможное, возможно, или что весь парадокс просто построен на недостатках мышления.
А вы сможете понять, в чем недостаток каждого из ниже перечисленных парадоксов?
12. Парадокс Ольберса
В астрофизике и физической космологии парадокс Ольберса – это аргумент, говорящий о том, что темнота ночного неба конфликтует с предположением о бесконечной и вечной статической Вселенной. Это одно из свидетельств нестатической Вселенной, такое, как текущая модель Большого взрыва. Об этом аргументе часто говорят как о “темном парадоксе ночного неба”, который гласит, что под любым углом зрения с Земли линия видимости закончится, достигнув звезды.
Чтобы понять это, мы сравним парадокс с нахождением человека в лесу среди белых деревьев. Если с любой точки зрения линия видимости заканчивается на верхушках деревьев, человек разве продолжает видеть только белый цвет? Это противоречит темноте ночного неба и заставляет многих людей задаться вопросом, почему мы не видим только свет от звезд в ночном небе.
11. Парадокс всемогущества
Парадокс состоит в том, что если существо может выполнять какие-либо действия, то оно может ограничить свою способность выполнять их, следовательно, оно не может выполнять все действия, но, с другой стороны, если оно не может ограничивать свои действия, то это что-то, что оно не может сделать.
Это, судя по всему, подразумевает, что способность всемогущего существа ограничивать себя обязательно означает, что оно действительно ограничивает себя. Этот парадокс часто формулируется в терминологии авраамических религий, хотя это и не является обязательным требованием.
Одна из версий парадокса всемогущества заключается в так называемом парадоксе о камне: может ли всемогущее существо создать настолько тяжелый камень, что даже оно будет не в состоянии поднять его? Если это так, то существо перестает быть всемогущим, а если нет, то существо не было всемогущим с самого начала.
Ответ на парадокс заключается в следующем: наличие слабости, такой, как невозможность поднять тяжелый камень, не попадает под категорию всемогущества, хотя определение всемогущества подразумевает отсутствие слабостей.
10. Парадокс Сорита
Парадокс состоит в следующем: рассмотрим кучу песка, из которого постепенно удаляются песчинки. Можно построить рассуждение, используя утверждения:
— 1000000 песчинок – это куча песка;
— куча песка минус одна песчинка – это по-прежнему куча песка.
Если без остановки продолжать второе действие, то, в конечном счете, это приведет к тому, что куча будет состоять из одной песчинки. На первый взгляд, есть несколько способов избежать этого заключения. Можно возразить первой предпосылке, сказав, что миллион песчинок – это не куча. Но вместо 1000000 может быть сколь угодно другое большое число, а второе утверждение будет верным при любом числе с любым количеством нулей.
Таким образом, ответ должен прямо отрицать существование таких вещей, как куча. Кроме того, кто-то может возразить второй предпосылке, заявив, что она верна не для всех “коллекций зерна” и что удаление одного зерна или песчинки все еще оставляет кучу кучей. Или же может заявить о том, что куча песка может состоять из одной песчинки.
9. Парадокс интересных чисел
Утверждение: нет такого понятия, как неинтересное натуральное число.
Доказательство от противного: предположим, что у вас есть непустое множество натуральных чисел, которые неинтересны. Благодаря свойствам натуральных чисел, в перечне неинтересных чисел обязательно будет наименьшее число.
Будучи наименьшим числом множества его можно было бы определить как интересное в этом наборе неинтересных чисел. Но так как изначально все числа множества были определены как неинтересные, то мы пришли к противоречию, так как наименьшее число не может быть одновременно и интересным, и неинтересным. Поэтому множества неинтересных чисел должны быть пустыми, доказывая, что не существует такого понятия, как неинтересные числа.
8. Парадокс летящей стрелы
Данный парадокс говорит о том, что для того, чтобы произошло движение, объект должен изменить позицию, которую он занимает. В пример приводится движение стрелы. В любой момент времени летящая стрела остается неподвижной, потому как она покоится, а так как она покоится в любой момент времени, значит, она неподвижна всегда.
То есть данный парадокс, выдвинутый Зеноном еще в 6 веке, говорит об отсутствии движения как таковом, основываясь на том, что двигающееся тело должно дойти до половины, прежде чем завершить движение. Но так как оно в каждый момент времени неподвижно, оно не может дойти до половины. Этот парадокс также известен как парадокс Флетчера.
Стоит отметить, что если предыдущие парадоксы говорили о пространстве, то следующий парадокс – о делении времени не на сегменты, а на точки.
7. Парадокс Ахиллеса и черепахи
В данном парадоксе Ахиллес бежит за черепахой, предварительно дав ей фору в 30 метров. Если предположить, что каждый из бегунов начал бежать с определенной постоянной скоростью (один очень быстро, второй очень медленно), то через некоторое время Ахиллес, пробежав 30 метров, достигнет той точки, от которой двинулась черепаха. За это время черепаха “пробежит” гораздо меньше, скажем, 1 метр.
Затем Ахиллесу потребуется еще какое-то время, чтобы преодолеть это расстояние, за которое черепаха продвинется еще дальше. Достигнув третьей точки, в которой побывала черепаха, Ахиллес продвинется дальше, но все равно не нагонит ее. Таким образом, всякий раз, когда Ахиллес будет достигать черепаху, она все равно будет впереди.
Таким образом, поскольку существует бесконечное количество точек, которых Ахиллес должен достигнуть, и в которых черепаха уже побывала, он никогда не сможет догнать черепаху. Конечно, логика говорит нам о том, что Ахиллес может догнать черепаху, потому это и является парадоксом.
Проблема этого парадокса заключается в том, что в физической реальности невозможно бесконечно пересекать поперечно точки – как вы можете попасть из одной точки бесконечности в другую, не пересекая при этом бесконечность точек? Вы не можете, то есть, это невозможно.
Но в математике это не так. Этот парадокс показывает нам, как математика может что-то доказать, но в действительности это не работает. Таким образом, проблема данного парадокса в том, что происходит применение математических правил для нематематических ситуаций, что и делает его неработающим.
6. Парадокс Буриданова осла
Это образное описание человеческой нерешительности. Это относится к парадоксальной ситуации, когда осел, находясь между двумя абсолютно одинаковыми по размеру и качеству стогами сена, будет голодать до смерти, поскольку так и не сможет принять рациональное решение и начать есть.
Парадокс назван в честь французского философа 14 века Жана Буридана (Jean Buridan), однако, он не был автором парадокса. Он был известен еще со времен Аристотеля, который в одном из своих трудов рассказывает о человеке, который был голоден и хотел пить, но так как оба чувства были одинаково сильны, а человек находился между едой и питьем, он так и не смог сделать выбора.
Буридан, в свою очередь, никогда не говорил о данной проблеме, но затрагивал вопросы о моральном детерминизме, который подразумевал, что человек, столкнувшись с проблемой выбора, безусловно, должен выбирать в сторону большего добра, но Буридан допустил возможность замедления выбора с целью оценки всех возможных преимуществ. Позднее другие авторы отнеслись с сатирой к этой точке зрения, говоря об осле, который столкнувшись с двумя одинаковыми стогами сена, будет голодать, принимая решение.
5. Парадокс неожиданной казни
Судья говорит осужденному, что он будет повешен в полдень в один из рабочих дней на следующей неделе, но день казни будет для заключенного сюрпризом. Он не будет знать точную дату, пока палач в полдень не придет к нему в камеру. После, немного порассуждав, преступник приходит к выводу, что он сможет избежать казни.
Его рассуждения можно разделить на несколько частей. Начинает он с того, что его не могут повесить в пятницу, так как если его не повесят в четверг, то пятница уже не будет неожиданностью. Таким образом, пятницу он исключил. Но тогда, так как пятница уже вычеркнута из списка, он пришел к выводу, что он не может быть повешенным и в четверг, потому что если его не повесят в среду, то четверг тоже не будет неожиданностью.
Рассуждая аналогичным образом, он последовательно исключил все оставшиеся дни недели. Радостным он ложится спать с уверенностью, что казни не произойдет вовсе. На следующей неделе в полдень среды к нему в камеру пришел палач, поэтому, несмотря на все его рассуждения, он был крайне удивлен. Все, что сказал судья, сбылось.
4. Парадокс парикмахера
Предположим, что существует город с одним мужским парикмахером, и что каждый мужчина в городе бреется налысо: некоторые самостоятельно, некоторые с помощью парикмахера. Кажется разумным предположить, что процесс подчиняется следующему правилу: парикмахер бреет всех мужчин и только тех, кто не бреется сам.
Согласно этому сценарию, мы можем задать следующий вопрос: парикмахер бреет себя сам? Однако, спрашивая это, мы понимаем, что ответить на него правильно невозможно:
— если парикмахер не бреется сам, он должен соблюдать правила и брить себя сам;
— если он бреет себя сам, то по тем же правилам он не должен брить себя сам.
3. Парадокс Эпименида
Этот парадокс вытекает из заявления, в котором Эпименид, противореча общему убеждению Крита, предположил, что Зевс был бессмертным, как в следующем стихотворении:
Они создали гробницу для тебя, высший святой
Критяне, вечные лжецы, злые звери, рабы живота!
Но ты не умер: ты жив и будешь жив всегда,
Ибо ты живешь в нас, а мы существуем.
Тем не менее, он не осознавал, что, называя всех критян лжецами, он невольно и самого себя называл обманщиком, хотя он и “подразумевал”, что все критяне, кроме него. Таким образом, если верить его утверждению, и все критяне лжецы на самом деле, он тоже лжец, а если он лжец, то все критяне говорят правду. Итак, если все критяне говорят правду, то и он в том числе, а это означает, исходя из его стиха, что все критяне лжецы. Таким образом, цепочка рассуждений возвращается в начало.
2. Парадокс Эватла
Это очень старая задача в логике, вытекающая из Древней Греции. Говорят, что знаменитый софист Протагор взял к себе на учение Эватла, при этом, он четко понимал, что ученик сможет заплатить учителю только после того, как он выиграет свое первое дело в суде.
Некоторые эксперты утверждают, что Протагор потребовал деньги за обучение сразу же после того, как Эватл закончил свою учебу, другие говорят, что Протагор подождал некоторое время, пока не стало очевидно, что ученик не прикладывает никаких усилий для того, чтобы найти клиентов, третьи же уверены в том, что Эватл очень старался, но клиентов так и не нашел. В любом случае, Протагор решил подать в суд на Эватла, чтобы тот вернул долг.
Протагор утверждал, что если он выиграет дело, то ему будут выплачены его деньги. Если бы дело выиграл Эватл, то Протагор по-прежнему должен был получить свои деньги в соответствии с первоначальным договором, потому что это было бы первое выигрышное дело Эватла.
Эватл, однако, стоял на том, что если он выиграет, то по решению суда ему не придется платить Протагору. Если, с другой стороны, Протагор выиграет, то Эватл проигрывает свое первое дело, поэтому и не должен ничего платить. Так кто же из мужчин прав?
1. Парадокс непреодолимой силы
Парадокс непреодолимой силы представляет собой классический парадокс, сформулированный как “что происходит, когда непреодолимая сила встречает неподвижный объект?” Парадокс следует воспринимать как логическое упражнение, а не как постулирование возможной реальности.
Согласно современным научным пониманиям, никакая сила не является полностью неотразимой, и не существует и быть не может полностью недвижимых объектов, так как даже незначительная сила будет вызывать небольшое ускорение объекта любой массы. Неподвижный предмет должен иметь бесконечную инерцию, а, следовательно, и бесконечную массу. Такой объект будет сжиматься под действием собственной силы тяжести. Непреодолимой силе потребуется бесконечная энергия, которая не существует в конечной Вселенной.
Решение парадокса отсутствующего доллара, парадокса Монти Холла и других известных парадоксов
Что такое парадокс? Проще говоря, парадокс — это аргумент, вывод которого не может существовать из-за преобладающих условий, изложенных в аргументе, но существует из-за тех же самых условий. Хотя не все парадоксы имеют потрясающие последствия, многие могут иметь интересные последствия для нашей жизни. Во всяком случае, они предлагают новую точку зрения и, возможно, пробуждают пытливую природу ума.
Парадокс пропавшего доллара
Я помню, как мне говорили об этом несколько раз в юности, и он приносил мне каждые раз. Посмотрим, достанет ли он и вам. Три человека едут в отель и снимают номер за 30 долларов. Когда они поднимаются на лифте, клерк понимает, что допустил ошибку и должен был списать с них всего 25 долларов. Он посылает посыльного, чтобы вернуть людям 5 долларов, с которых они переплатили. Но когда лифт поднимается, коридорный понимает, что они не знают, что получают возмещение, и кладет себе в карман 2 доллара.Подойдя к двери отеля, он объясняет предполагаемую завышенную цену в 3 доллара и передает деньги. Это означает, что каждый человек заплатил всего 9 долларов, в общей сложности 27 долларов. Но у посыльного есть 2 доллара, что дает нам в общей сложности 29 долларов. Где этот недостающий доллар?
Ответ кроется в числовом смысле: мы не должны делать 27 + 2, потому что на самом деле мы сделали 27-2. Это потому, что у нас было 30 и мы убрали в общей сложности 5, но люди ушли только из 3, удаляемых из общего количества, но формулировка задачи заставляет нас думать, что у нас было 27, и снова добавили 2 в это.У нас действительно есть новое общее количество в 27, и мы получили , что , добавив два к 25, которые должны были быть начислены им. Я знаю, что это объяснение кажется подозрительным, но просмотрите его еще раз. Все дело в правильном переводе ситуации (А1 3).
Парадокс Монти Холла
Этот парадокс был известен еще до того, как Монти Холл стал ассоциироваться с ним в своем игровом шоу Давайте заключим сделку , но он дает такой нелогичный результат, что даже Разрушители мифов взялись за него! Первоначально она была названа Мартином Гарднером «Задача трех заключенных», но впервые была опубликована в колонке «Математические игры» журнала Scientific American в 1959 году.Версия, которую мы здесь обсудим, является той, с которой сталкивались многие: базовая установка из игрового шоу (А1 9)
Представьте, что вы участник игрового шоу, и ведущий представляет вам три двери. За одной из этих дверей — невероятный приз, а за двумя другими — ничего. Ведущий просит вас выбрать одну из дверей, что вы и делаете, а затем показывает вам пустую дверь. Теперь хозяин предложит вам остаться с выбором или переключиться на другую оставшуюся дверь. Большинство людей думают, что это не имеет значения или что это всего лишь кадр 50/50, и поэтому придерживаются своего первоначального выбора.Но, как оказалось, при смене дверей у вас есть 2/3 шанса на победу! Как такое возможно?
Ключ — в разбивке вариантов и результатов, которые у вас есть. Если вы выбрали дверь 1 и не переключились, то может произойти одно из трех. Если приз меньше 1, то вы выиграли. Если приз позади 2, то ведущий показал 3, и вы проиграли с 1. Если приз меньше 3, то ведущий показал 2, и вы проиграли с 1. Таким образом, у вас есть 1/3 шанса на победу.Но что, если вы выберете дверь 1, а затем переключитесь? Если он действительно был позади 1, то черт возьми, вы проиграли. Если он был позади 2, вы переключились с 1, и ведущий показал 3, так что вы выиграли. Если он был позади 3, вы переключились с 1, и хост показал 2, так что вы выиграли. Это действительно не 1/2 шанса, а 2/3 шанса. Имейте это в виду, когда в следующий раз будете играть в такую игру! (Al 16-7)
Парадокс Барбера Рассела
Этот парадокс был разработан известным математиком Бертраном Расселом, чьи работы в области логики и теории множеств широко распространены и используются до сих пор.Он придумал этот парадокс, чтобы описать интересный аспект теории множеств.
Представьте себе город, полный людей, которым нужна стрижка. Никому не разрешается стричь волосы, но, к счастью, в городе есть парикмахер. Он действительно стриг всем волосы, как и обещал, но теперь ему нужна стрижка, потому что он житель города, и им всем нужна стрижка. Но он не может стричь свои волосы, потому что никому не разрешается стричь свои волосы. Чем он занимается?
В этом примере что-то является членом набора, но, будучи членом этого набора, не может существовать в нем.Если бы был изготовлен специальный набор для парикмахеров, то с ним все было бы хорошо, но, поскольку он заключен в городе, он не может нарушать это правило.
Парадокс коробки Бертрана
Это парадокс, который я часто вижу в качестве подарка детям, поэтому можно подумать, что это пустяк. Но обратите пристальное внимание. Представьте, что у вас есть три коробки, в каждой по 2 объекта. Все коробки запечатаны, и в одном есть два объекта. Как в нем, в другом — два объекта B, а в последнем — объект A и объект B.Вероятность того, что вы выберете коробку AB, составляет 1/3, как и ожидалось. Но что, если я выберу коробку наугад и посмотрю только на одну из вещей внутри? Каков шанс, что я действительно выбрал ящик AB? Что ж, если это A, тогда у вас нет коробки BB, так что вероятность ½. Точно так же, если вы выбрали B, то это не бокс AA и, следовательно, вероятность ½. Как знание одного факта может изменить шанс того, что он был 1/3, а теперь ½? В конце концов, у меня осталось еще три варианта, верно? Что ж, подумайте об этом так: есть варианты 3 A и 3 B.Если вы выберете один из этих трех, остается 2/3 шанса, что оставшийся не находится внутри коробки, но только половина из оставшихся вариантов может иметь статус двойного объекта. Половина 2/3 дает мне… 1/3, все хорошо! (Ал 4-5).
Парадокс дня рождения
Хотя это раздвигает границы парадокса, это, безусловно, противоречивый результат, на который стоит внимательно взглянуть. Представьте, что у нас есть комната, полная людей, и я хочу знать, сколько их нужно, чтобы получить снимок 50/50 на двух человек, имеющих один день рождения.Интуиция заставляет нас чувствовать, что нам нужно более 366 на все дни года. Но, как выясняется, нам нужно всего 23 человека! Но все становится еще страннее! Если бы я хотел шанс 99%, почти наверняка, мне нужно всего 57 человек. Что здесь происходит ? (Al 6-7)
Подумайте о вероятности того, что приведете человека в комнату, и у него не будет одного дня рождения. Вероятность того, что у двух людей не один и тот же день рождения, будет 364/365, потому что только 1 день в году будет общим для них.А теперь введите третье лицо. Теперь вероятность того, что ни у кого из них не будет общего дня рождения, будет (363/365) * (364/365), а пока мы должны исключить 2 дня, которые могут быть общими. Если убрать это число с 1 (100%), мы получим вероятность того, что у них будет один и тот же день. Если мы расширим эту технику, мы обнаружим, что около 23 — человек, наконец, получим шанс лучше, чем 50/50. Просто потрясающе (7-8).
цитируемых работ
Аль-Халили, Джим. Парадокс: девять величайших загадок физики .Бродвейские книги в мягкой обложке, Нью-Йорк, 2012: 3-9, 16-7. Распечатать.
.
Парадоксы Зенона

 |
| Парменид Элейский (общественное достояние) |
Даже если вы думаете, что не слышали о них по имени, вы узнаете их. Самый известный из парадоксов Зенона гласит, что я не могу подойти к вам, потому что сначала мне нужно пройти половину пути, а как только я это сделаю, мне все равно придется преодолеть половину оставшегося расстояния, а как только я доберусь туда, мне придется преодолеть половину оставшегося расстояния — до бесконечности. Есть бесконечное количество промежуточных точек, так что по логике я никогда не смогу добраться до них. Но это легко доказать, просто сделав это, что мы все можем сделать. Итак, у нас есть парадокс, противоречие, что-то, что должно быть правдой, но явно нет. Существует ли решение, которое адекватно рассматривает противоречивые явления? Некоторые говорят, что есть; некоторые говорят, что нет.
Зенон Элейский был греческим философом, родившимся около 490 г. до н.э., и был приверженцем Парменида, основателя элейской школы мысли на территории современной южной Италии.Зенон выжил как персонаж в диалоге Платона под названием « Парменид, », и из этого мы знаем, что такое элеатская школа и откуда Зенон пришел со своими парадоксами. Парменид учил (частично), что физический мир, как мы его воспринимаем, является иллюзией, и что единственное, что действительно существует, — это постоянное, неизменное целое, которое он назвал «Единым Существом». То, что мы воспринимаем как движение, вовсе не является физическим движением, а просто различными интерпретациями или проявлениями Единого Существа.Лично я думаю, что в элейской школе курили много травки, но Зенон был вовлечен в это и придумал свои парадоксы, чтобы поддержать взгляд Парменида на мир. Парадоксы Зенона были призваны доказать, что движение должно быть невозможно, поэтому Парменид должен быть прав.
Считается, что он разработал в общей сложности около девяти таких парадоксов, но они никогда не были опубликованы. Самыми известными и интересными являются его три парадокса движения:
Во-первых, парадокс Ахилла и черепахи, сумевших устроить бег.Ахиллес, зная, что он быстрее, дал черепахе стометровую фору. За то время, которое потребовалось Ахиллу, чтобы преодолеть сотню метров, черепаха переместилась на десять, так что, когда Ахилл добрался туда, он обнаружил, что черепаха все еще была впереди. За то время, что Ахиллес пробежал эти десять, черепаха переместилась еще на метр. Независимо от того, сколько раз Ахиллес продвигался к последней позиции черепахи, черепаха поползла еще немного вперед к тому времени, когда он там оказался. Хотя Ахиллес казался более быстрым бегуном, ему было невозможно когда-либо поймать черепаху.
Второй и самый известный — это так называемый парадокс дихотомии, в котором мы неоднократно раздираем пополам каждое расстояние, которое нужно преодолеть. Чтобы Гомер добрался до автобусной остановки, он должен пройти полпути. По прибытии он должен пройти половину оставшегося расстояния и так далее, и так далее, оставив 1/8 расстояния, затем 1/16, затем 1/32, затем 1/64; у него будет бесконечный запас оставшихся расстояний для путешествия, и поэтому он никогда не сможет добраться до остановки.
Третий парадокс — это парадокс Флетчера, который обнаруживает, что все его стрелы вообще не могут двигаться.В любой момент времени стрела неподвижна в полете. В этот застывший момент стрела вообще не может двигаться, потому что у нее нет времени, чтобы сделать это. Время состоит из бесконечной последовательности моментов, в каждом из которых стрела не может двигаться. Нигде мы не можем найти данный момент, в который стрела бы успела переместиться, и поэтому независимо от того, сколько таких мгновений у нас есть, стрела не может ни лететь, ни упасть на землю.
Парадоксы Зенона часто преподносятся некоторыми людьми как свидетельство того, что физика или наука ошибаются.Если древнегреческий философ может описать простую ситуацию, которая, как подсказывает наша интуиция, очевидно, верна, нам легко придать ей большее значение, чем запутанный беспорядок, который представляет собой современная наука. Почему мы должны слушать Эйнштейна, который дает нам множество непостижимых уравнений, когда изящные басни Зенона доказывают, что физический мир не такой, каким его должно быть наука? Учитывая эту цепочку рассуждений, неудивительно, что Зенон стал чем-то вроде любимца для некоторых сторонников Нью Эйдж духовной, а не физической вселенной.
Известно, что, услышав парадоксы, коллега-философ по имени Диоген Циник просто встал, прошелся и снова сел. Мой парень. Его ответ, возможно, был бойким, но он элегантно опроверг утверждение Зенона. По крайней мере, в нем опровергались физические последствия утверждения, но не затрагивались философские аспекты; и не предоставил математических решений.
Парадоксы Зенона — интересное пересечение математики и философии. Математически легко вычислить, когда и где Ахиллес настигнет черепаху, но философский аргумент остается (по-видимому) неразрешимым.Бертран Рассел описал парадоксы как «неизмеримо тонкие и глубокие». Итак, философы предприняли довольно интересные попытки решить эту проблему.
Одна из таких тактик касается длины Планка, которая является наименьшей возможной единицей длины в системе Планка. Все единицы Планка основаны на универсальных физических константах, таких как скорость света и гравитационная постоянная. С философской точки зрения достаточно точно описать планковскую длину как квант расстояния, наименьшую возможную единицу.Это означает, что на ипподроме Ахилла и черепахи, а также между Гомером и автобусной остановкой существует конечное число отрезков Планка (хотя и ошеломляюще большое их количество). Не может быть бесконечного количества очков, и поэтому Гомер в конце концов сможет прийти. Однако, хотя это звучит так, как будто это могло бы элегантно решить парадокс, это не так. Невозможно навязать квантовое решение геометрической задаче. Простая иллюстрация того, почему это так, — это вообразить очень маленький прямоугольный треугольник с двумя равными сторонами, каждая из которых равна одной планковской длине.Гипотенуза должна быть равна √2 планковской длины, что невозможно. Планк здесь не применяется. Несмотря на попытки прийти к иному выводу, мы — это , имея дело с бесконечностями. Или … это мы?
Интуитивно мы понимаем, что 0,9 (0,9999999 …) — это значение, которое всегда приближается к 1, но никогда не достигает его. Это нормально как концепция и мысленный эксперимент, но математически неверно. 0,9 фактически равно 1; это просто два разных способа записи одного и того же значения.Это легко доказать, удовлетворив большинство людей, разделив оба значения на 3. И 1 ÷ 3, и 0,9 ÷ 3 равны 0,3, следовательно, оба равны друг другу. Другой способ взглянуть на это — рассмотреть дробь 1/9, которая равна 0,1. 2/9 равно 0,2, и так далее, вплоть до 8/9 = 0,8 и 9/9 = 0,9, и все мы знаем, что 9/9 = 1. Когда мы делим число 1 на 9 равных частей , этот верхний срез проходит ровно до 1, конечного и достижимого числа.
Если это раскручивает ваш мозг внутри черепа, знайте, что вы уже принимаете многие другие интерпретации той же идеи.Рассмотрим любое другое число, десятичное значение которого представляет собой бесконечный повторяющийся ряд, скажем 3/7. Оно равно 0,428571, и мы все согласны с тем, что он равен 3/7, а не «числу, приближающемуся к 3/7, но никогда не достигающему его». Это два способа написать одно и то же.
Это та же концепция, когда Гомер делает последний шаг и опускает ногу, завершая свой путь к автобусной остановке. Он не совершил бесконечное путешествие. Мы можем написать уравнение, которое описывает, как его последний шаг состоит из бесконечно повторяющейся серии все меньших и меньших дробей, как сказал Зенон:
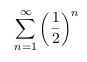
Мы в братстве называем это абсолютно сходящимся рядом, а , вопреки пониманию Зенона , равно 1.
Другое широко предлагаемое решение, особенно для парадокса Флетчера, включает время и скорость. Зенон, обвиняет своих критиков, рассматривал только расстояния и геометрию; и поскольку он полностью исключил время из своих парадоксов, он также исключил скорость, поскольку скорость является функцией расстояния и времени. Когда тело находится в движении, его положение всегда меняется. Движение плавное, это не серия прыжков от точки к точке. Следовательно, в любой момент времени движущееся тело не имеет единственного точного положения.Гипотеза Зенона о том, что стрела всегда застыла в какой-то точке, не может быть обнаружена, воспроизведена или вычислена, поскольку вещи движутся не так. Представьте, что вы фотографируете движущийся объект. Всегда будет размытие в движении. Независимо от того, насколько быстрым будет затвор вашей камеры, даже бесконечно малым, всегда будет небольшое размытие. Нет такой вещи, как застывшая во времени движущаяся стрела.
Точно так же расчет Зенона, согласно которому Ахиллес никогда не поймает черепаху, также не учитывает время.Предпосылка Зенона предполагает, что каждый сегмент гонки, на котором Ахиллес продвигается к предыдущему положению черепахи, занимает некоторое время; а поскольку таких сегментов бесконечно много, Ахиллесу потребуется бесконечное количество времени. Это тоже неправильно. По мере того, как физическая длина каждого сегмента уменьшается экспоненциально в сходящемся ряду, уменьшается и время, необходимое Ахиллу, чтобы пройти его. Время Ахилла поймать черепаху представлено сходящейся серией, равной конечному числу.
Ахиллес будет поймать черепаху, потому что сама последовательность сегментов, предложенная Зеноном, составляет конечное расстояние, которое Ахиллес преодолеет за конечное время.
Homer будет добраться до автобусной остановки, потому что все эти бесконечно сложные дробные сегменты представляют собой абсолютно сходящийся ряд, равный конечному расстоянию.
Стрела Флетчера всегда в движении после выстрела, ни в какой момент времени она никогда не застывает в фиксированном положении, из которого у нее нет времени двигаться.
Итак, если обобщить парадоксы Зенона, это, по сути, словесные игры, основанные на легко понимаемой математической концепции. Нет никакого парадокса, потому что математика Зенона была неправильной.

Брайан Даннинг
Следуйте @BrianDunning
Цитируйте эту статью:
Даннинг, Б. «Парадоксы Зенона». Подкаст Skeptoid. Skeptoid Media,
19 июля 2011 г. Web.
23 августа 2020 г.
.
Paradoxes by mental-free на DeviantArt
Есть два вида парадоксов:
1. Парадоксы могут быть правдивыми утверждениями, которые кажутся противоречащими друг другу (которые я люблю называть литературными парадоксами)
2. Парадоксы могут быть более научными, например те, кто явно нарушает научные законы
, или истинные утверждения, которые не имеют никакого смысла.
Начнем с примера литературного парадокса. Это один из
самых известных парадоксов за всю историю, возможно, вы даже сможете распознать его.«Этот приговор
— ложь». Если это предложение верно, то это ложь. А если ложь, то
— ложь, значит, это правда. Непонятно, а?
Один «научный парадокс» — это нарушение
давнего закона о том, что информация не может быть уничтожена. (Я знаю, что сейчас вы
говорите: «Психически здоровый, должно быть, идиот, я удаляю информацию со своего компьютера все
раз».) Это не тот случай, в этом справочнике информация означает значение
и / или энергия. Черные дыры, кажется, нарушают этот закон, потому что их огромная немыслимая гравитация
(см. Мою статью о Черных дырах) имеет точку, в которой ничто, не
, даже самая быстрая вещь во Вселенной, не может избежать этой точки.Таким образом, материя
или энергия, предположительно проходящая через горизонт событий, потеряна для Вселенной, поскольку не
, даже «противодействующий взрыв» ВСЕЙ энергии, присутствующей во Вселенной, вытащит ее
из горизонта событий. (Примечание: «противодействующий взрыв» — это взрыв непосредственно перед
или позади объекта, чтобы изменить его траекторию.) У этого парадокса есть много предположительных решений
, одно из которых связано с потерей массы из-за излучения Хокинга, а
возможное исчезновение черной дыры через такое.Радиация Хокинга — это примерно
, самая странная и трудная для понимания вещь, которую я слышал некоторое время. Излучение Хокинга
— это когда энергия, которая в какой-то момент двигалась по касательной к горизонту события
, и была захвачена на кажущейся постоянной орбите. Гравитация и угловой импульс
частицы, вращающейся вокруг горизонта событий со скоростью 186 282 миль
в секунду, заставляет энергию производить две частицы, одну частицу, а другую — античастицу
. Затем они разделяются, в то время как одна частица падает в черную дыру
, а другая убегает, потому что она отправляется по траектории в сторону от сингулярности.
Черная дыра потеряла крошечный кусочек массы. Этому бесконечно малому количеству потерянной материи
потребуются триллионы или квадриллионы лет, чтобы полностью рассеять черную дыру
, но когда это произойдет, энергия и масса, захваченная черной дырой, снова будут выпущены во Вселенную на
, таким образом защищая сохранение энергии
закон.
Есть много парадоксов, мои личные любимые имеют дело с бесконечностью,
потому что о бесконечности невозможно думать.Возьмем, к примеру, теорию «устойчивого состояния
». Эта теория о Вселенной и ее происхождении в основном утверждает:
«Вселенная всегда была, есть и всегда будет». Примечание: обычно
означает бесконечность. Итак, попробуйте подумать об этом. Вселенная существует
бесконечных года и будет существовать бесконечность. Особенно тот факт, что Вселенная
существует уже бесконечное количество лет. Невозможно думать о
или постигать на каком-либо более глубоком уровне. Удивительно, да? Давай попробуем другой.Скажем, есть
отеля с бесконечным количеством комнат, полностью заполненных. Если еще бесконечное количество людей желает, чтобы в отеле остановилось
человек, что делает менеджер? Фактический ответ — попросить всех удвоить комнату, в которой они находятся. Итак, люди из комнаты 1 переходят в комнату 2, люди из комнаты 2 переходят в комнату 4, и так до бесконечности. Затем бесконечные комнаты теперь доступны для бесконечных людей. Сгибание мозгов, да? Но так весело.
Хорошо, теперь парадокс моей собственной разработки. Что такое 1/10 бесконечности? Остается ли 1/10 бесконечности
бесконечностью? Неужели 1/10 бесконечности меньше 1/9 бесконечности?
Любой, кто действительно думал об этом и хочет серьезно обсудить это, напишите мне комментарий.
Психически-свободный
.

