5 логических головоломок на поиск закономерностей — Лайфхакер
Догадайтесь, какие связи есть между буквами и числами в примерах, а потом заполните ячейки со знаком вопроса.
– 1 –
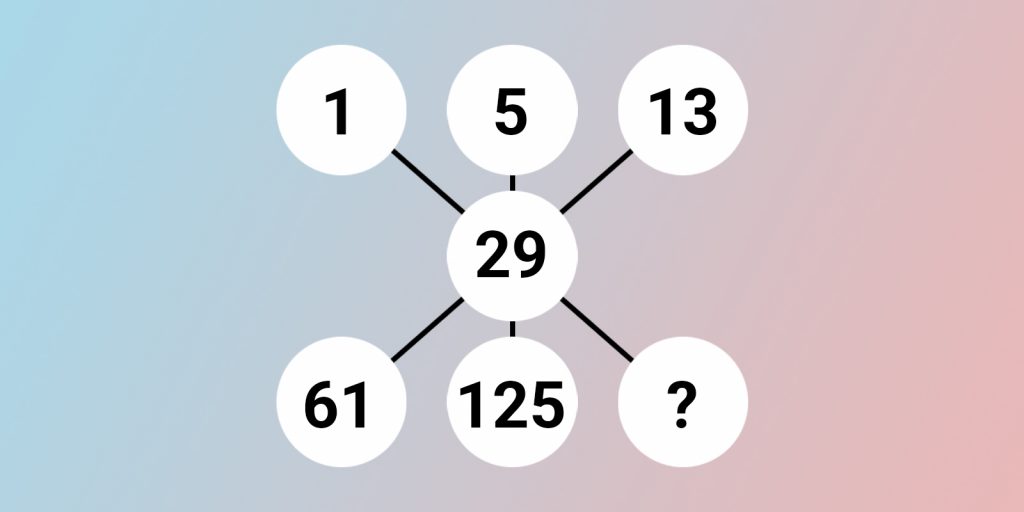
Определите, какое число должно стоять на месте знака вопроса.
Показать ответ
Скрыть ответ
Вместо знака вопроса в кружочке должно стоять число 253. Вот по какому принципу образуются числа в кружочках: каждое предыдущее умножается на 2, а к результату прибавляется 3.
1 × 2 + 3 = 5.
5 × 2 + 3 = 13.
13 × 2 + 3 = 29.
29 × 2 + 3 = 61.
61 × 2 + 3 = 125.
125 × 2 + 3 = 253.
Или вот ещё один способ решения: к каждому предыдущему числу прибавляется 2 в n‑й степени.
1 + 22 = 1 + 4 = 5.
5 + 23 = 5 + 8 = 13.
13 + 24 = 13 + 16 = 29.
29 + 25 = 29 + 32 = 61.
61 + 26 = 61 + 64 = 125.
125 + 27 = 125 + 128 = 253.
– 2 –
Определите, какая буква должна стоять на месте знака вопроса.

Показать ответ
Скрыть ответ
Вместо знака вопроса в квадрате должна стоять буква «П». Сумма чисел в каждом квадрате — это порядковый номер буквы в алфавите. Проверим:
6 + 4 + 4 = 14. «М» — четырнадцатая буква в алфавите. «Ё» тоже считаем!
4 + 1 + 7 = 12. «К» — двенадцатая буква в алфавите.
5 + 6 + 10 = 21. «У» — двадцать первая буква в алфавите.
1 + 14 + 2 = 17. «П» — семнадцатая буква в алфавите, которая и должна стоять на месте знака вопроса.
– 3 –
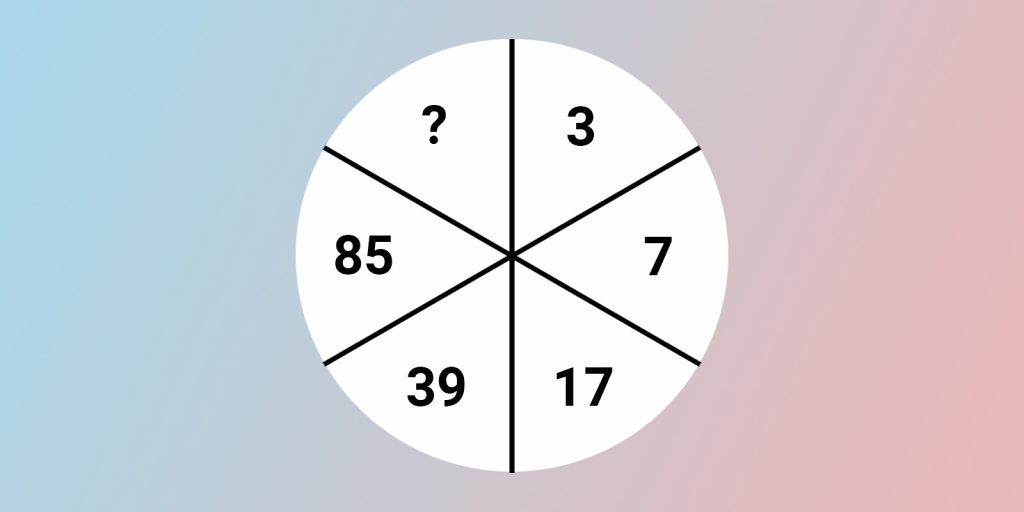
Определите, какое число должно стоять на месте знака вопроса.
Показать ответ
Скрыть ответ
Вместо знака вопроса должно стоять число 179. Если двигаться по часовой стрелке начиная с 3, то каждое последующее число равно удвоенному предыдущему, к которому прибавили 1, 3, 5, 7, 9.
3 × 2 + 1 = 7.
7 × 2 + 3 = 17.
17 × 2 + 5 = 39.
39 × 2 + 7 = 85.
85 × 2 + 9 = 179.
– 4 –
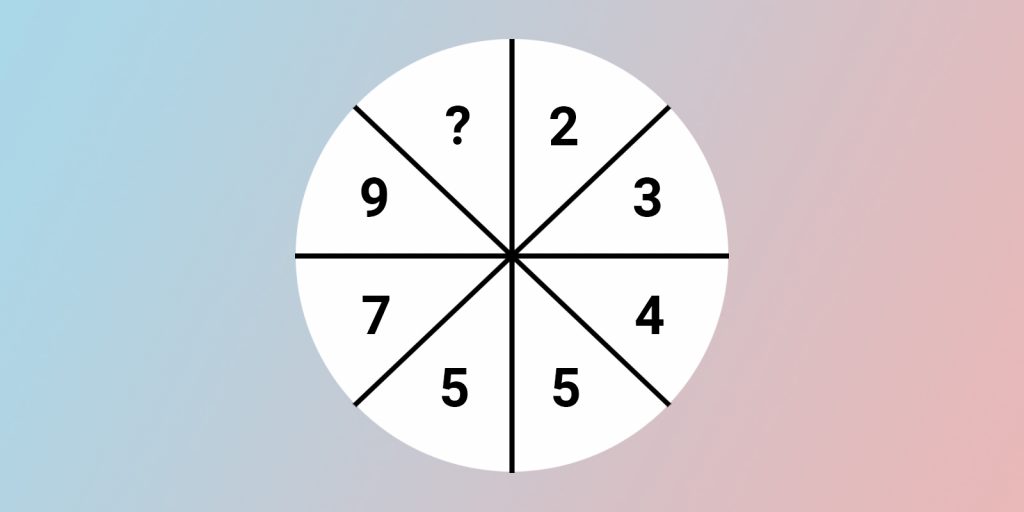
Определите, какое число должно стоять на месте знака вопроса.
Показать ответ
Скрыть ответ
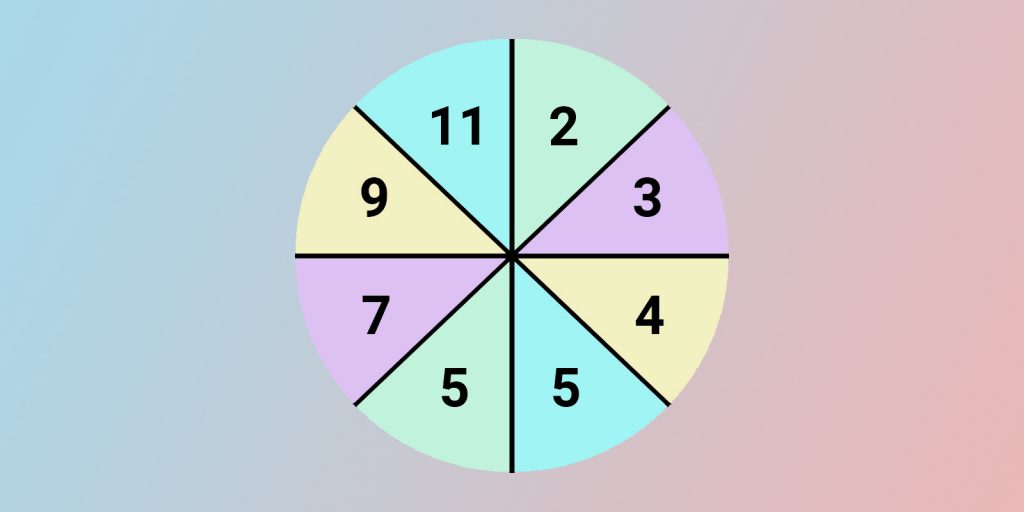
Вместо знака вопроса должно стоять число 11. Чтобы получить каждое число из левой половины круга, мы берём число из противоположного сектора, удваиваем и добавляем единицу.
5 = 2 × 2 + 1.
7 = 3 × 2 + 1.
9 = 4 × 2 + 1.
11 = 5 × 2 + 1.
– 5 –
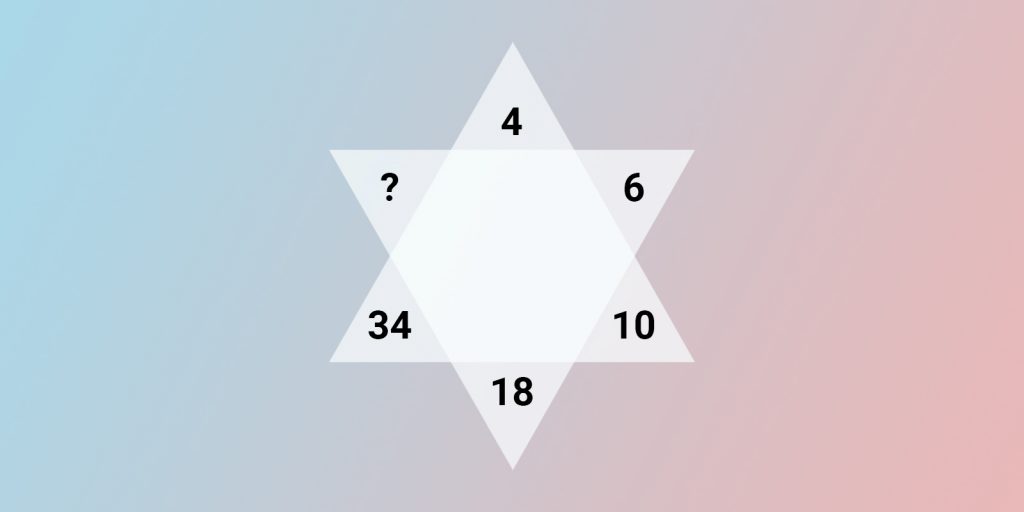
Определите, какое число должно стоять на месте знака вопроса.
Показать ответ
Скрыть ответ
Вместо знака вопроса должно стоять число 66. Если двигаться по часовой стрелке начиная с 4, каждое последующее число равно удвоенному предыдущему, из которого вычли двойку.
4 × 2 − 2 = 8 − 2 = 6.
6 × 2 − 2 = 12 − 2 = 10.
10 × 2 − 2 = 20 − 2 = 18.
18 × 2 − 2 = 36 − 2 = 34.
34 × 2 − 2 = 68 − 2 = 66.
Сколько задач решили без подсказок? Рассказывайте в комментариях!
Читайте также
🤔
Математики нашли закономерность, разбираясь в том, как избежать её появления
Мы, наконец, узнали, насколько большим должно быть множество чисел, чтобы в нём гарантировано содержалась закономерность под названием «многочленная прогрессия»
Некоторые закономерности в математике настолько редкие, что их можно искать всю жизнь и не найти. Другие же встречаются так часто, что их, кажется, невозможно избежать.
Новое доказательство, представленное Сарой Пилюс из Оксфордского университета, показывает, что одна численная закономерность особенно важного типа, по сути, является неизбежной: она гарантированно обнаружится в любой достаточно большой коллекции чисел, вне зависимости от того, как их выбирают.
«Этим закономерностям присуща своего рода неразрушимость», — сказал Теренс Тао из Калифорнийского университета в Лос-Анджелесе.
Доказательство Пилюс касается последовательности чисел под названием «многочленные прогрессии». Их легко создавать – вы очень быстро сможете составить свою – и они касаются связи между сложением и умножением чисел.
Несколько десятилетий математики знали, что при малом размере набора (или «множества») чисел – то есть, когда в нём содержится относительно немного чисел – в нём может вообще не оказаться никаких многочленных прогрессий. Им также было известно, что при росте множества оно в конце концов переходит определённый порог, после которого в нём уже содержится так много чисел, что одна из таких последовательностей обязана там встретиться. Это похоже на миску супа с буковками из теста – чем больше у вас букв, тем больше вероятность, что из них можно складывать слова.
Но до работы Пилюс математики не знали, каков этот порог. Её доказательство даёт ответ на этот вопрос – точную формулу, определяющую, насколько большим должно быть множество, чтобы в нём гарантированно содержались определённые многочленные прогрессии.
А до этого у математиков были только смутные представления о том, что многочленные прогрессии встречаются среди целых чисел (1, 2, 3, и т.п.). Теперь они точно знают, где их искать.
В поисках закономерностей
Чтобы представить себе эти закономерности, рассмотрим одну из них, немного более простую, чем та, с которой работала Пилюс. Начнём с цифры 2 и будем добавлять тройку: 2, 5, 8, 11, 14, и т.д. Такая закономерность – начав с одного номера, добавляем другой – называется «арифметической прогрессией». Это одна из наиболее изученных и частых прогрессий в математике.
Касательно частоты появления арифметической прогрессии среди целых чисел нужно понять две вещи.
Одну из них доказал Эндре Семереди в 1975 году. Сначала, сказал он, выберите длину своей арифметической прогрессии. Это может быть закономерность с четырьмя членами (2, 5, 8, 11), или семью (14, 17, 20, 23, 26, 29, 32), или вообще с любым количеством. После этого он доказывает, что как только множество чисел достигает определённого размера (который он не смог определить), в нём обязательно найдётся арифметическая прогрессия такой длины. Таким образом он укрепил идею о том, что в достаточно больших множествах чисел где-то обязательно найдётся закономерность.
«Семереди, по сути, сказал, что полный беспорядок невозможен. Какое бы множество вы ни взяли, в него всегда сумеет затесаться какая-нибудь структура», — сказал Бен Грин из Оксфорда.
Однако теорема Семереди ничего не говорит о том, насколько большой должна быть коллекция чисел для того, чтобы эти закономерности стали неизбежными. Он просто сказал, что для арифметической прогрессии любой выбранной длины обязательно существует множество чисел неизвестного размера, которое его содержит.
Более чем через два десятилетия после этого математики определили этот размер – доказав таким способом второй основной факт, касающихся арифметических закономерностей.
В 2001 году Тимоти Гауэрс из Кембриджского университета доказал, что если вы хотите гарантированно найти, допустим, арифметическую прогрессию из пяти членов, вам нужно множество чисел по меньшей мере определённого размера – и определил, какой это будет размер (описать точный размер сложно, в эту формулу входят огромные экспоненциальные числа).
Чтобы понять, что сделал Гауэрса, нужно понять, что имеют в виду математики, говоря о «размере» множества чисел и об идее «достаточно большого размера».
Во-первых, выберите интервал на числовой прямой, допустим, от 1 до 1000, или что-то более случайное, типа от 17 до 1016. Начало и конец интервала не имеют значения, важна только его длина. Затем определите ту долю чисел из этого интервала, которую вы хотите добавить в множество. К примеру, если вы создаёте множество из 100 чисел от 1 до 1000, то размер вашего множества составит 10% от интервала.
Доказательство Гауэрса работает вне зависимости от того, как вы выбираете числа из этого множества. Можно взять 100 первых нечётных чисел из диапазона от 1 до 1000, 100 первых чисел, заканчивающихся на 6, или даже 100 случайных чисел. И Гауэрс доказал, что вне зависимости от метода, как только множество займёт достаточно большое пространство (не обязательно 10%) в достаточно длинном интервале, в нём неизбежно появится арифметическая прогрессия из пяти членов. То же самое он доказал для арифметической прогрессии любой длины.
«После Гауэрса мы знаем, что если мне дадут арифметическую прогрессию любой длины, тогда любое подмножество» чисел какого-то определённого размера обязательно будет содержать эту прогрессию, сказала Пилюс.
Работа Пилюс похожа на достижение Гауэрса, только она сконцентрировалась на многочленных прогрессиях.
В арифметической прогрессии мы выбираем одно начальное число и добавляем к нему другое. В том виде многочленной прогрессии, который изучала Пилюс, вы выбираете начальное значение, и добавляете к нему степени другого числа. К примеру: 2, 2 + 31, 2 + 32, 2 + 33, 2 + 34. То есть, 2, 5, 11, 29, 83. В её прогрессии тоже было только по одному члену для каждой степени – это требование упрощает работу с ними.
Эти многочленные прогрессии тесно связаны с такой важной закономерностью, как геометрическая прогрессия, которая формируется возведением числа во всё большую степень: 31, 32, 33, 34,… Они естественным образом появляются во многих областях математики и физики, и восхищают математиков уже несколько тысячелетий. Геометрические прогрессии реже встречаются даже в крупных множествах чисел, однако если её немного подправить – допустим, добавив константу к каждому члену – получится многочленная прогрессия. А вот они как раз, кажется, появляются повсюду.
«Можно создавать большие множества чисел, не содержащие геометрических прогрессий. Но если дать себе немного свободы, и сдвинуть геометрическую прогрессию», создав многочленную прогрессию, то крупные множества, кажется, просто вынуждены содержать их, сказал Шон Прендивиль из Ланкастерского университета, работавший с Пилюс над многочленными прогрессиями.
В 1996 году Виталий Бергельсон и Александр Лейбман доказали, что при достижении достаточно большого размера множеством там обязательно должны появиться многочленные прогрессии – это был многочленный эквивалент работы Семереди. Однако, у математиков не было понятия о том, насколько большим должно быть «достаточно большое» множество.
Пилюс ответила на этот вопрос контринтуитивным способом – размышляя о том, какими свойствами должно обладать множество чисел, чтобы в нём не было таких закономерностей.
Борьба с закономерностями при помощи закономерностей
Пилюс хотела определить, насколько большим должно быть множество – какой процент чисел из интервала должен в нём содержаться – чтобы гарантировать, что оно будет содержать заданную многочленную прогрессию. Для этого она представила все способы, благодаря которым множество чисел может избежать появления в нём прогрессии – а потом доказала, что при превышении определённого размера не работают даже самые хитроумные из этих стратегий.
Эту задачу можно рассматривать как состязание. Допустим, кто-то просит вас создать множество, содержащее половину чисел от 1 до 1000. Вы выигрываете, если в множестве не будет первых четырёх членов многочленной прогрессии. Как бы вы подбирали числа?
Сара Пилюс из Оксфордского университета
Возможно, вы инстинктивно попытаетесь выбрать числа случайным образом. Но этот инстинкт будет ошибочным.
«Большинство множеств находятся в середине нормального распределения. Они содержат среднее количество многочленных прогрессий», — сказал Прендивиль. И это среднее значение гораздо больше требуемого от вас нулевого.
Это похоже на то, как если бы вы выбирали из всего населения планеты случайного человека, и получили такого, рост которого близок к среднему. Если ваша цель – найти более редкий экземпляр ростом более 2 м, вам нужно вести поиски более направленно.
Поэтому для выигрыша в состязании по выбору чисел вам нужен более организованный способ решать, какие числа включать в ваше множество из 500 штук. К примеру, можно заметить, что если выбирать только чётные числа, можно устранить вероятность того, что в множестве будут находиться многочленные прогрессии, содержащие нечётные числа. Прогресс! Естественно, таким способом вы увеличиваете вероятность того, что ваше множество содержит многочленные прогрессии, состоящие из чётных чисел.
Однако суть в том, что придумав структурированный способ выбора 500 чисел, можно устранить вероятность нахождения в множестве определённых многочленных прогрессий. Иначе говоря, нужно соблюдать закономерность, чтобы избежать закономерности.
Пилюс решила доказать, что при достижении определённого размера, даже очень хитроумно составленным множествам всё равно придётся включить в себя многочленные прогрессии. По сути, она хотела определить критическую точку, в которой вы, каждый раз избегая включения многочленных прогрессий одного типа, приходите к наличию многочленных прогрессий другого типа – как в случае с чётными и нечётными числами.
Для этого ей нужно было найти способ количественно оценить структуризацию множества.
Измерение структуры
До выхода работы Пилюс многие математики пытались понять, когда именно многочленные прогрессии появляется в множестве чисел. Этим занимались многие из весьма успешных математиков, но никто из них не смог достаточно сильно продвинуться на пути к выяснению размера множества, которого оно должно достичь, чтобы содержать многочленные прогрессии различной длины.
Главным препятствием для них было то, что математики не представляли, как именно можно охарактеризовать структуры, позволяющие избежать появления многочленных прогрессий. Была одна потенциальная техника для этого, но когда Пилюс начинала работать в этой области, её нельзя было применить к вопросам, касающимся многочленных прогрессий.
Эта техника появилась в работе Гауэрса от 2001 года по арифметическим прогрессиям. Гауэрс создал тест, назвав его «нормой Гаэурса», обнаруживающий структуры определённого вида в множестве чисел. Тест выдаёт одно число, определяющее количество структурности в множестве – то есть, он численно показывает, насколько далеко множество отошло от простого набора случайных чисел.
«Понятие »множество выглядит случайным» не является чётко определённым с математической точки зрения», — сказал Грин. Гауэрс нашёл способ количественно охарактеризовать это понятие.
Множество может быть более или менее структурированным. Множества, содержащие случайные числа, не имеют структуры, поэтому с большой вероятностью содержат числовые закономерности. У таких множеств норма Гауэрса низкая. Множества, содержащие только нечётные числа, или только числа, делящиеся на 10, имеют рудиментарную структуру. Легко доказать, что при превышении определённого размера в множествах такой простой структуры также появятся различные закономерности.
Тяжелее всего работать с множествами очень сложных структур. Они могут выглядеть случайными, однако при этом быть построенными по какому-то очень хитрому правилу. Их норма Гауэрса высока, и они дают наилучшие шансы систематически избегать закономерностей при росте размера множества.
Поскольку Гауэрс использовал эти техники для поисков ответы на вопросы, связанные с арифметическими прогрессиями, их нельзя было применить к вопросам, касающимся многочленных прогрессий. Арифметические прогрессии имеют равные промежутки, а числа в многочленных прогрессиях очень активно скачут. Нормы Гауэрса были полезными для изучения многочленных прогрессий так же, как триммер для травы для очистки старой краски с дома: идея похожая, хотя для этой работы и не совсем подходит.
В новом доказательстве Пилюс использовала базовую идею нормы Гауэрса для создания нового способа анализа структур, связанных с многочленными прогрессиями. Она использовала технику «понижения градуса» для доказательства того, что при разбирательствах с интересующими её многочленными прогрессиями стоит беспокоиться только о простых структурах с низкой нормой Гауэрса. Дело в том, что многочленные прогрессии настолько сильно меняются при переходе от одного члена к другому, что они неизбежно прорываются через менее прочные числовые препятствия – как слон, продирающийся через витрины наружу из посудной лавки.
Формулу Пилюс тяжело описать простыми терминами. В ней участвует двойной логарифм длины изначального интервала, из которого вы выбираете числа для своего множества. Полученный ею минимальный размер не обязательно будет самым малым из всех возможных – в будущих работах может обнаружиться, что истинный порог находится ещё ниже. Но до появления её доказательства у математиков вообще не было количественного понимания появления гарантии наличия многочленных прогрессий.
«Она стала первым человеком, показавшим, насколько большим должен быть размер множества», — сказал Прендивиль.
Доказательство Пилюс количественно отвечает на один вопрос, связанный с многочленными прогрессиями. Теперь математики используют его в надежде получить ответ на другой вопрос – касательно того, когда многочленные прогрессии появляются в множествах, целиком состоящих из простых чисел, наиболее важных чисел в математике, упорно сопротивляющихся каким бы то ни было последовательностям. До появления этого доказательства у математиков не было представления о том, как подойти к этому вопросу.
«Есть надежда, что некоторые из аргументов моей работы можно будет применить в области простых чисел», — сказала Пилюс.
Поиск и эксплуатация закономерностей
На рынке имеются различные группы участников, каждая из которых ведёт свою игру. Сфокусируемся на одной из них, достаточно многочисленной или обладающей достаточным капиталом, чтобы влиять на цену. Мы хотим увидеть закономерности в действиях этой группы и как-то начать эксплуатировать их в свою пользу.
В следующем ниже тексте я хочу с помощью аналогий и мысленного эксперимента показать, что это трудная задача, и пояснить, почему.
Если бы влияние всех остальных групп участников было мало, то нашу ситуацию можно было бы свести к игре против единственного оппонента. Утрируя, будем считать, что оппонент двигает цену либо вверх (+1), либо вниз (-1), а мы пытаемся предугадать это и успеть заранее купить перед движением цены вверх и продать перед движением вниз. Если мы угадали, то получаем прибыль, если не угадали, то убыток. Ещё можно не играть, а просто наблюдать за оппонентом.
Начнём с тривиального примера. Допустим, что мы видим серию действий оппонента:
+1, +1, -1, +1, +1, -1, +1, +1,- 1, …
Простая закономерность, которая тут видна: +1 встречается чаще, чем -1, поэтому надо просто покупать каждый раз, и у нас уже будет какая-то прибыль.
Более сложная закономерность: после двух +1 идёт одна -1, поэтому надо два раза купить, потом один раз продать. Прибыль будет втрое больше.
Примеры могут быть посложнее, где закономерности менее очевидны. Однако разного рода подходы вроде частотного анализа, анализа корреляций, поиска паттернов (после такой-то последовательности из k действий идёт такое-то действие) и прочие могут принести положительный результат.
Бывают, конечно, теоретические «зубодробительные» варианты закономерностей, например:
+1,+1,-1,+1,+1,+1,-1,-1,+1,+1,+1,-1,+1,+1,+1,+1,…
(я взял десятичное разложение числа пи = 3,1415… и нечётные цифры закодировал +1, а чётные -1). Вряд ли догадаешься о такой закономерности: у неё нет корреляций, нет частотных перекосов и паттернов, выглядит случайно, но является полностью детерминированной.
Это я к тому, что даже в отсутствии помех разгадывать действия оппонента может быть тяжело.
А теперь вспомним, что на рынке есть другие участники, которые своими действиями создают немалые колебания цены. По своему масштабу они могут быть сильно больше, чем от действий оппонента, на котором мы сфокусировались. Из-за этого в результате наблюдений мы видим не последовательность из +1 и -1 типа:
+1, +1, -1, …,
а примерно такое:
+1±случайное число, +1±случайное число, -1±случайное число, …,
причём случайное число может быть, скажем, порядка 10.
Наблюдая такое, нам даже трудно понять, что за действия совершал наш оппонент, поскольку шум всё портит.
Если считать, что шум имеет нулевое математическое ожидание (не известно, так ли это), то нам придётся долго усреднять все наблюдения, чтобы понять, есть ли у действий оппонента частотный перекос. Для первой закономерности в начале текста это удастся сделать.
Если же оппонент действовал так:
+1, -1,+1, -1, +1, -1,
то мы не найдём частотного перекоса, собирая статистику по всем наблюдениям. Тут надо предположить, что чётные действия оппонент делает одним образом, нечётные – другим, собрать два набора статистических данных, убедиться, что в каждом случае есть перекос и уже потом заниматься эксплуатацией.
Но оппонент может действовать по более сложным закономерностям. И чтобы их выявить, нам придётся проявить фантазию, сгенерировать много гипотез, проверить каждую из них статистически, не попасть в ситуацию (подгонки под историю), когда из множества гипотез какие-то случайно проходят статистический тест, а потом уже эксплуатировать.
И последний аргумент, усложняющий ситуацию, состоит в том, что оппонент может поменять своё поведение: действовал по одной закономерности, а стал действовать по другой или вообще ушёл с рынка. После этого все наши усилия по сбору статистических данных не просто пошли прахом, а ещё и могут мешать, давая ложную уверенность.
Отдельно стоит вопрос о том, откуда брать гипотезы о действиях оппонента. Для рынка все видят один и тот же график, но на разных таймфреймах. Как тут выделить, на что обращает внимание оппонент и как он может действовать?
Если кому есть, что сказать по любому из затронутых поводов, то пишите свои комментарии.
ML для поиска закономерностей по Atamanу.
Жил был такой трейдер Ataman и были у него критерии робастности системы: фичей не больше трех и параметры фича не должна выглядеть «тут читаю, тут не читаю, тут рыбу заворачиваю». В чем проблема когда мы используем нейросети, или там случайный лес или градиентый бустинг? В том это условие внутрь не засунуть, нейросеть (случайный лес) будет использовать все фичи, и нарежет их, как захочет, хоть в мелкую стружку. Что делать и как с этим бороться?
Я сделал три цикла с GradientBoosting, и ограничил глубину деревьев 3. Вуаля!
Здесь можно посмотреть как это выглядит на питоне + база данных+ код WealthLab.
Результаты?
Ну вот например на тренировочной выборке 2010-04.2018 нашлось такое:
if ((AroonDownClose_20_[Bar] >= 75.0)&&(AroonDownClose_20_[Bar] <= 100.0)) //
if ((StochD14_5_[Bar] >= 1.9416)&&(StochD14_5_[Bar] <= 10.3487)) //
Загоняем, считаем:
| Названия строк | Коли | Profit % |
| test | 374 | 0,36 |
| 2006 | 17 | 0,50 |
| 2007 | 43 | 0,83 |
| 2008 | 79 | 0,04 |
| 2009 | 35 | 0,52 |
| 2018 | 61 | 0,56 |
| 2019 | 87 | 0,41 |
| 2020 | 52 | -0,03 |
| train | 647 | 0,88 |
| 2010 | 57 | 1,89 |
| 2011 | 78 | 0,59 |
| 2012 | 65 | 0,55 |
| 2013 | 112 | -0,33 |
| 2014 | 85 | 2,45 |
| 2015 | 85 | 0,40 |
| 2016 | 56 | 1,86 |
| 2017 | 89 | 0,26 |
| 2018 | 20 | 2,28 |
| Общий итог | 1021 | 0,69 |
Видим что если на трайне доходность была 0,88, то на тесте доходность упала до 0,36. Таки дела. По графику видно что это система из разряда «ловли ножа». Дело такое
Или вот система только с одной фичей:
if ((TRIXClose_10_[Bar] >= -4.0825)&&(TRIXClose_10_[Bar] <= -0.799)) //
| Названия строк | Коли | Profit % |
| test | 154 | -0,13 |
| 2006 | 11 | 7,03 |
| 2007 | 7 | 6,07 |
| 2008 | 72 | -9,41 |
| 2009 | 29 | 9,29 |
| 2019 | 3 | 5,51 |
| 2020 | 32 | 7,86 |
| train | 176 | 4,35 |
| 2010 | 12 | 5,29 |
| 2011 | 47 | 6,37 |
| 2012 | 18 | -2,32 |
| 2013 | 24 | 0,22 |
| 2014 | 46 | 6,07 |
| 2015 | 6 | 5,76 |
| 2016 | 4 | 1,12 |
| 2017 | 10 | 4,64 |
| 2018 | 9 | 8,24 |
| Общий итог | 330 | 2,26 |
Тут с трейна доходность в 4,35 упала до теста -0,13. «Виноват» 2008 год с его 72 сделками по -9,41%.
Тоже система из разряда «ловля ножей».
Ну вот как то так
Предложения со словосочетанием ПОИСК ЗАКОНОМЕРНОСТЕЙ
Целью научного исследования является обоснование теории диалектического развития отечественной судебной системы и поиск закономерностей её формирования.
Соответственно, все эти разделы, взятые в своём историческом аспекте, могут составить предмет диахронической теории семиосферы, в задачу которой войдёт выявление динамики связей между знаковыми средствами различных типов и уровней и поиск закономерностей в изменениях их соотношений.
Что же, раз исход в единичном испытании непредсказуем, для поиска закономерностей учёные стали исследовать частоту появления тех или иных исходов в длинной серии независимых экспериментов, связывая её с вероятностью.
Материалистический подход многих процессуальных археологов, которые, казалось, дегуманизировали прошлое в поисках закономерностей изменения культур, неизбежно вызвал реакцию его оппонентов.
Задачей исследователей становился поиск закономерностей или констант в художественном облике местности, которые должны были проявляться в течение длительного периода времени, на протяжении веков.

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова программатор (существительное):
Кристально
понятно
Понятно
в общих чертах
Могу только
догадываться
Понятия не имею,
что это
Другое
Пропустить
Начинать работу в этом направлении следует с поиска закономерностей.
Нумерология использует числовые символы и геометрические фигуры как «основной инструментарий» для поиска закономерностей.
Конечно, звёздное небо — с его постоянством и цикличностью перемен — с древних времён вдохновляло на поиск закономерности.
Конечно птицы — благодатная модельная группа для поиска закономерностей поведения животных и движущих сил биологической эволюции.
Это аспекты изучения коммуникации у животных, проблемы использования этологических признаков в систематике животных и реконструкциях филогенетических взаимоотношений внутри таксонов, вопросы, связанные с гибридизацией, поиск закономерностей и тенденций в эволюции акустических и социальных систем, и поведения животных в целом.
Прагматик не считает неправильным проверить работу законов движения путём преобразования его в табличные данные и поиска закономерностей в этих таблицах.
Вы начинаете искать в этих данных некий волшебный ключ к рынку через анализ ценовых потоков, через наблюдение графиков, через поиск закономерностей, повторяющихся особенностей и паттернов.
Анализ изменчивости головного указателя и размеров головы от 5 до 15 лет при малочисленности групп является малоинформативным, всё это препятствовало поиску закономерностей развития детского организма на восходящем этапе онтогенеза.
Педагогика развивалась вместе с человечеством и прошла длительный путь поиска закономерностей, методов, средств и форм обучения и воспитания людей, оформилась в научно обоснованную систему знаний.
Такие задания стимулируют обучающихся к проведению несложных обоснований, к поиску закономерностей.
Теперь начнём поиск закономерности «нота буква алфавита».
Наш мозг отлично воспринимает информацию через органы чувств и изучает её в поисках закономерностей, однако нам очень плохо удаётся описать или вычислить, каким образом мы это делаем, особенно когда большой объём быстро меняющейся информации поступает к нам в достаточно быстром темпе.
Правильный ответ в таких случаях требует подлинного мастерства в поиске закономерностей и сложной коммуникации.
Но взамен получил огромный материал для поиска закономерностей в движениях цен…
В итоге мы с членами исследовательской группы в поисках закономерностей проанализировали результаты более чем 750 исследований и обнаружили два типа, как ни странно, не всегда взаимосвязанных самоосознания.
Потому что математика — это в первую очередь поиск закономерностей, идёт ли речь о предсказании погоды или прогнозе роста городов, о формулировании космологических законов или поведении субатомных частиц.
Одна из них, неотделимая от массового повседневного исторического сознания, опирается на многовековую традицию и в новейшее время идентифицирует себя с философией уникальности и идиографичности исторического знания, исключающего перспективу поиска закономерности и видящего организующий момент такого знания лишь в ценностном выборе историка как познающего субъекта.
Динамический метод, напротив, изучает явления в процессе их изменения во времени и направлен на поиск закономерностей этих изменений.
Особенно наш мозг ящера, склонный к поиску закономерностей и обращению к опыту, что делает его эффективной системой для добывания пищи и воспроизведения успешных поведенческих моделей.
Будет показано, что часть нашего мозга ориентирована на прошлый опыт и поиск закономерностей, и это порой заставляет нас покупать, когда цены иррационально высоки, и продавать, когда цены иррационально низки.
Интуитивный трейдинг — это метод торговли, основанный на наблюдении за рынком, поиске закономерностей и создании метода восприятия — системы понимания поведения рынка.
Подсознание может оказать очень большую помощь в поиске закономерностей.
Научные интересы кафедры охватывают распознавание образов и прогнозирование, поиск закономерностей в массивах данных (data mining), комбинаторные и алгебраические методы синтеза и анализа алгоритмов, прикладные системы распознавания и прогнозирования; имитационное моделирование.
Долгие наблюдения, сравнения и поиски закономерностей привели к тому, что в рамках нумерологии как системы появилась концепция вибрирующих чисел.
Игра на внимание «Посчитай — не ошибись», упражнение на поиск закономерности числового ряда, упражнение «Проверь себя», работа в группах «Продолжи ряд», упражнение на нахождение закономерности в серии фигур, задание на смекалку.
Поиск закономерностей развития отношений, который в контексте наук и искусств осуществляется по-разному, преследует одну и ту же цель: найти оптимальную стратегию поведения, жизни, которая позволила бы минимизировать страдание и максимизировать творческую отдачу.
Узнав эти пропорции, мы можем начать поиск закономерностей, типичных для бестселлеров.
На наш взгляд, именно структурализм (как школа и как метод) с его поиском закономерностей в текстах разного рода вывел гуманитарное знание на новый уровень научности.
— Давай на потом оставим поиск закономерностей, а сейчас, Танюша, ответь мне на вопрос, что ты будешь пить?
Социологи помогают историкам осуществлять поиск закономерностей и причинно-следственных связей.
Поэтому энциклопедический элемент был подчинён задачи поисков закономерностей.
Вторая категория астрологов — «продолжающие» или «ссылающиеся» астрологи — уже не утруждают себя поиском закономерностей и пытаются позаимствовать их у предшественников.
Она оценила картину в целом в поисках закономерности.
Мыслители на протяжении веков осуществляли поиски закономерностей соответствия человеческой психики и физиологии.
Один из способов, которым мозг отличает значимую информацию от незначимой — это поиск закономерностей и концентрация внимания на них.
Одно яркое следствие (или, может быть, причина) нашей склонности к поиску закономерностей — это то, что наш мозг плохо переносит неопределённость.
Поиск закономерностей — это, определённо, последствие эволюции: если вы замечали, что членов семьи съедали львы, когда они уходили одни, вы не пойдёте один сами.
Где, самое главное, не допускается их приучение к самостоятельному мышлению, действию, и поиску закономерностей.
Неточные совпадения:
Поиски скрытых закономерностей, лежащих в основе всех осознанных попыток личностного развития, — это крайне сложная задача, так как её решение должно быть общим и абстрактным, но при этом давать нам разнообразные возможности практического применения.
Состязательный процесс и розыскной — две исторические формы, каждая из которых зародилась и существовала в определённых условиях, но закономерности цивилизационного развития преодолевают ограниченность конкретных условий и выявляют главные тенденции развития — от замкнутости к общности, от противопоставления интересов к поиску точек их соприкосновения и к совместной их реализации.
Задачи прикладных теорий: поиск средств для достижения намечаемых обществом практических целей, путей и способов использования познанных фундаментальными теориями законов и закономерностей.
Любовь и предательства, поиски призвания, случайности и закономерности в нашей судьбе… Эти темы вновь и вновь вдохновляют меня, переплавляясь в сюжетные новеллы, в искусство вымысла.
Она имеет более чем 40-летнюю историю и динамично развивается, в то время как теория стратегического государственного управления находится только в стадии формирования, поиска основных принципов, закономерностей, подходов, методов управления и т.
Последующее понимание этих закономерностей неизбежно приводит к необходимости поиска причин происходящего вовне и внутри себя.
Теория стратегического внутрифирменного управления (стратегического менеджмента) является ключевой, объясняющей и предсказывающей перспективы развития фирм в условиях рыночной экономики, имеет более чем 40-летнюю историю и динамично развивается, в то время как теория стратегического государственного управления находится только в стадии формирования, поиска основных принципов, закономерностей, подходов, методов управления.
Результатом поиска ответов на подобные вопросы являются предположения, которые опираются на вскрытые тенденции развития политического явления, на существующие общие закономерности общественного развития.
Важно то, что выработанное в процессе занятий стремление фиксировать выделенные и осознанные закономерности в слове ведёт к активному поиску детьми способов словесного выражения, к использованию всех имеющихся у них речевых возможностей.
Из этого не следует, что всё и всегда активно участвовали в поисках каких-то закономерностей в природе или в метафизике.
Задачи прикладных теорий: поиск средств для достижения практических целей, путей и способов использования познанных фундаментальными теориями законов и закономерностей.
Все сказанное лишний раз подтверждает, что междисциплинарный статус проблемы личности выступает как необходимое условие поиска системных закономерностей развития человека в биогенезе, социогенезе и онтогенезе, а не повод к растворению психологии личности в других естественных или социальных науках.
Эти годы, полные исследований, бессонных ночей перед компьютером, проверкой всё новых и новых теорий, появляющихся с завидной степенью регулярности, отработкой новых закономерностей и поиском «рыночных неэффективностей», проходят незаметно, но в итоге, прошедший столь сложный путь человек, зачастую не добивается цели, поставленной им много лет назад.
Его полную характеристику невозможно дать без поправки на следующие качественно меняющиеся параметры социального поля: 1) состояние и изменение социальной и правовой реальности; 2) наличие коррелятивных связей между процессом социальной трансформации в форме глобализации и появлением, изменением или расширением сущности, форм, способов и методов преступной деятельности; 3) определение причин и закономерностей такой связи и степень её отражения в действующих системах национально-государственных законодательств и международных актов; 4) поиск эффективных форм борьбы с современной преступностью, в том числе через изменение социально-экономических условий, методами активного социального контроля и всей совокупностью мер уголовного права.
Иногда они выбираются по наитию, но всё же модельеры в своём творческом труде и поиске учитывают определённые закономерности.
7. Методика «установление (поиск) закономерностей»
Сущность задания
состоит в поиске слов с определенным
(заданным) порядком и количеством букв.
Обратимся
к примерам:
5 | 4 | 3 | 2 | 1 | ||
1. | Х ! Х | КОТ | КОК | РОК | РОТ | — |
2. | ? O | МАША | КАША | РАМА | МАМА | — |
3. | — ? : — | СОДА | КРОТ | БРОД | СОРТ | — |
В начале каждой
строки стоят условные знаки – Х (икс),
0 (ноль), $, :, ?, !. Этими знаками «закодированы»
(или обозначены) количество и порядок
букв в одном из слов данной строки,
которое Вам и нужно отыскать.
Например, в начале
первого задания стоят знаки «Х ! Х». Это
значит, что нужно найти слово из трех
букв, в котором две крайние буквы
одинаковые. В примере таким словом
является «КОК». Верный ответ в графе
«4».
Во
втором задании необходимо найти слово,
в котором 1 и 3 и 2 и 4 буквы одинаковые
(«? O
? O»).
Таким словом является «МАМА». Верный
ответ в графе «2».
В третьем задании
1 и 4 буквы одинаковые, а 2 и 3 разные.
Верного ответа нет. Значит, метка
ставится в графе «1».
В каждой строке
может быть приведен только один верный
ответ или его может не быть совсем.
Все задания
выполняются по порядку сверху – вниз.
На
выполнение задания отводится 8
минут.
СТИМУЛЬНЫЙ БЛАНК К МЕТОДИКЕ 7 «УСТАНОВЛЕНИЕ
ЗАКОНОМЕРНОСТЕЙ»
5 | 4 | 3 | 2 | 1 | ||
1. | Х ! + Х | РАНА | КРОТ | ВОСК | ТОРТ | — |
2. | + ! ? = | ЖАРА | КИЛЬ | СОУС | ОВОД | — |
3. | Х * ! * | ВЕРА | СОЛО | КОНЬ | РОСТ | — |
4. | ? — ? + | СЕНО | КОРТ | ЛАВА | ОБОИ | — |
5. | ! * * Х | ПИЛА | ГОРЕ | ИГЛА | МОРЕ | — |
6. | = ? Х ? | ЛАПА | ОКНО | КОКС | МРАК | — |
7. | + ! + — | ВРАГ | ОБОД | ЛОСЬ | ЧАСЫ | — |
8. | = * Х = | СОУС | МОСТ | ГРАД | ЛИПА | — |
9. | ? ! Х * | БОРТ | КАША | ЖЕЛЕ | РОЖЬ | — |
10. | + ! ! + | ЛУНА | РОЗА | СОРТ | ВРАГ | — |
11. | = ! * Х + | АВТОР | РТУТЬ | ВАХТА | РОБОТ | — |
12. | + * = + Х | НОРКА | ССОРА | КОРКА | МЕССА | — |
13. | ! ? ! Х — | СЛОВО | СПОРТ | ОБРОК | ОСОБА | — |
14. | ? ! Х Х ! | КАССА | ЛАССО | МАССА | СУММА | — |
15. | * + * + Х | ГАЙКА | СЛОВО | ПЕПЕЛ | ОЛОВО | — |
16. | = ! ? ! + ? | ЗОЛОТО | МНЕНИЕ | БЕРЕЗА | КОРОВА | — |
17. | * + ! Х ? — | КРАСКА | ЗАНУДА | ПОЛЕНО | ШАХТЕР | — |
18. | = Х * ? ! Х | ЗАНОЗА | ТЮРБАН | ЦВЕТОК | КОЛЕСО | — |
19. | — ? * ? Х ? | СТАКАН | ТАЛАНТ | МОЛОКО | АНАНАС | — |
20. | ! = Х ! ? * | ПОЧЕРК | СПИСОК | КАПКАН | СУНДУК | — |
21. | * Х ! — + = ? | НОВИЧЕК | ВИРТУОЗ | РАЗЪЕЗД | ПОЛНОЧЬ | — |
22. | ! ? + = Х ! ? | КАЛИТКА | НАДЕЖДА | ТЕЛЕФОН | ПРЕСТИЖ | — |
23. | * Х ! Х ? Х = | СКАНДАЛ | ЗАЩЕЛКА | ВПАДИНА | ХОРОВОД | — |
24. | + * = ? = * — | ЛАУРЕАТ | СИНОНИМ | МАЛАХИТ | НАКИДКА | — |
25. | ! = ? = ! Х + | СЕЛЕНИЕ | РЕФЕРАТ | СИНОНИМ | РЕНТГЕН | — |
26. | ! — + = ? * : Х | КУЛЬТУРА | ТРАМПЛИН | РАСТЕНИЕ | ПАССАЖИР | — |
27. | — Х ? * ! ! * + | КОМИССИЯ | БИОЛОГИЯ | ПРОПАСТЬ | МОЛЕКУЛА | — |
28. | Х ? ! + ? * = * | РАЗВЕДКА | ПЕРЕМЕНА | ПРЕГРАДА | АРГУМЕНТ | — |
29. | ! * ? + * ? * ? | ПРОКУРОР | МЕХАНИЗМ | АНТИЛОПА | ХИТРОСТЬ | — |
30. | + Х — ! ? Х — = | ОБОЛОЧКА | ВОЛНЕНИЕ | ПРАКТИКА | ВНИМАНИЕ | — |
Синонимы к словосочетанию ПОИСК ЗАКОНОМЕРНОСТЕЙ
ПО́ИСК, -а, м. 1. мн. ч. (по́иски, —ов). Разыскивание, отыскивание кого-, чего-л. Поиски неприятеля. Поиски причины болезни. Отправиться на поиски.
Все значения слова «поиск»
ЗАКОНОМЕ́РНОСТЬ, -и, ж. Обусловленность объективными законами; существование и развитие соответственно законам (в 5 знач.
Все значения слова «закономерность»
Целью научного исследования является обоснование теории диалектического развития отечественной судебной системы и поиск закономерностей её формирования.
Соответственно, все эти разделы, взятые в своём историческом аспекте, могут составить предмет диахронической теории семиосферы, в задачу которой войдёт выявление динамики связей между знаковыми средствами различных типов и уровней и поиск закономерностей в изменениях их соотношений.
Что же, раз исход в единичном испытании непредсказуем, для поиска закономерностей учёные стали исследовать частоту появления тех или иных исходов в длинной серии независимых экспериментов, связывая её с вероятностью.- (все предложения)
Редизайн поиска: определение шаблонов и моделей поиска | Надя Цеч
📚 В книгах Шаблоны поиска и Пользовательский интерфейс поиска авторы описывают эти общие шаблоны и модели поиска:
Шаблон 1. Выйти из
Сценарий: Пользователь вводит запрос> видит результаты> завершает работу.
Может быть, они нашли то, что им нужно. Возможно, информация была неактуальной или результаты были ошеломляющими.Мы должны выяснить, почему они ушли, и как мы можем улучшить их опыт.
Выход из шаблона 1, Google.com. Я сразу вижу информацию. Я ухожу, потому что нашла то, что мне нужно. Схема выхода 2. Я искала «книги о дружбе». Я не вижу ничего стоящего. С меня хватит.
Сценарий: пользователь вводит запрос> видит результаты> сужает их.
«Второй по распространенности шаблон». Если вариантов слишком много или трудно определить, какой из них лучший, пользователям необходимо сузить результаты поиска с помощью фильтров, сортировки или расширенного поиска.
Узкий узор 1. На сайте Atlassian.com много продуктов. Чтобы найти нужную документацию, я использую фильтр и выбираю продукт, который меня интересует.
Сценарий: пользователь вводит запрос> видит результаты> открывает одну из первых ссылок.
Этот шаблон часто встречается, когда пользователи знают, что они ищут. Мы можем помочь им, добавив автозаполнение, распознавая синонимы, проверяя опечатки и предлагая альтернативные варианты.
Лучший первый образец 1, Goodreads. Я знаю название книги. Я использую поиск в основном для навигации.Лучший первый образец 1, Goodreads. Мы можем улучшить опыт, предлагая ярлыки.
Иногда пользователи точно знают, что ищут. Но это не значит, что для дизайнеров и разработчиков нет проблем. На изображении ниже показано, как люди пишут Бритни Спирс.
Marc.merlins.orgЛучший первый шаблон 1. Исправление опечаток — это функция, улучшающая восприятие.
Сценарий: пользователь вводит запрос> открывает один из результатов> открывает связанные ссылки внутри документа или использует термины из документа для запросов.
Этот шаблон часто встречается, когда пользователи ищут рекомендации или исследуют новые темы.
Схема выращивания жемчуга 1. Система рекомендаций Imdb.com.
Связанные ссылки на странице помогают изучить новую тему и найти фразы для запросов.
Схема выращивания жемчуга 2. Ссылки облегчают изучение новой темы. Wikipedia
Сценарий: пользователь вводит запрос> открывает первый результат> возвращается к поиску> открывает второй результат> возвращается к поиску> повторяет.
.
ZUP — Универсальный зигзаг с узорами Песавенто. Поиск выкройки
Введение
Многие трейдеры заинтересованы в поиске паттернов на ценовых графиках. Этот поиск можно выполнить с помощью индикаторной платформы ZUP. Есть несколько вариантов работы с платформой. Во-первых, вы можете искать известные шаблоны со строго заданными параметрами. Во-вторых, вы можете настроить параметры в соответствии с вашими требованиями. В-третьих, вы можете создавать свои собственные паттерны с помощью графического интерфейса ZUP и сохранять их параметры в файл.Эта возможность позволяет быстро проверить, можно ли найти эти новые паттерны на графиках.
Паттерны описывали многие авторы. Одним из них был Гарольд Гартли. Гартли опубликовал свою книгу «Прибыль на фондовых рынках» еще в 1935 году. Одна из страниц книги содержала изображение модели и краткое описание того, как ее можно использовать в торговле. Активное развитие этой идеи началось только спустя несколько десятилетий. Тогда было описано много новых паттернов. Один из самых известных авторов этих узоров — Скотт Карни.Карни разработал множество паттернов, включая Гартли, Летучую мышь, Бабочку, Краба и другие. Скотт Карни зарегистрировал авторские права на все эти шаблоны в 2016 году.
Существует множество алгоритмов поиска шаблонов. Например, вы можете выбирать экстремумы на графике, «растягивать» между ними сетку Фибоначчи и определять появление паттерна при достижении рынком определенных уровней. Этот алгоритм используется как для ручного поиска, так и в некоторых программах. Другой вариант — чисто программное решение.Алгоритм программы находит крайние точки, проверяет их взаимное расположение и, если это соответствует образцу, программа показывает соответствующее сообщение.
В индикаторной платформе ZUP реализовано множество возможностей для поиска паттернов. Их можно построить вручную. Но основной алгоритм — это автоматический поиск паттернов на экстремумах рынка, которые определяются с помощью различных зигзагов. В версиях ZUP до 151 режимы поиска паттернов задавались через параметры. Но существует более 100 параметров, которые могут повлиять на поиск закономерностей.Такое обилие параметров усложняет задачу. В версии 152 появилась новая опция: возможность использовать графический интерфейс. Основные настройки задаются через параметры, а быстрое подключение паттернов к поиску осуществляется с помощью графического интерфейса.
Для удобства все параметры разбиты на группы. Ниже представлены группы параметров, влияющих на поиск паттернов.
- Настройки зигзага.
- 1 — Параметры для уровней Фибо.
- 2 — Параметры паттернов Песавенто.
- 3 — Параметры для паттернов Гартли.
- 15 — Общие параметры.
Большое количество встроенных графических инструментов также может помочь в поиске закономерностей.
В первой части статьи я описываю, как шаблоны могут быть связаны для поиска через графический интерфейс в ZUP версии 152. Затем я объясняю параметры для поиска паттернов Гартли. Остальные паттерны кратко рассмотрены в конце статьи.
Часть первая. Графический интерфейс для работы с паттернами
В версии 152 добавлены элементы графического интерфейса для работы с паттернами. Графический интерфейс позволяет:
- Подключение и отключение паттернов от поиска;
- Просмотр изображений с помощью шаблонов пятиточечных узоров;
- Создание новых пятиточечных рисунков;
- Параметры редактирования пятиточечных рисунков;
- Сохранение отредактированных рисунков взамен старого или в отдельный *.CSV файл;
- Сохранение вновь созданного рисунка в новый или выбранный файл * .CSV;
- Подключение рисунков из выбранного файла к поиску;
- Создание списков шаблонов для поиска.
Параметр ExtPanel в конце списка параметров индикаторной платформы предназначен для работы с графическим интерфейсом ZUP. ExtPanel = true позволяет работать с графическим интерфейсом.
Если вы устанавливаете ExtPanel = true, но графический интерфейс не отображается или он был удален нажатием ESC, комбинация SHIFT-Z отобразит его.
Затем нажмите Insert. В следующем меню нажмите на «значок бабочки» -. Это открывает меню для работы с паттернами:
По сравнению с версией 151, этот содержит кнопку Выбрать. При нажатии на кнопку открывается следующее меню со списком:
Меню позволяет подключать паттерны из списка для поиска или отключать их без использования панели параметров индикатора. Это можно сделать, просто нажав соответствующую кнопку.Значения параметров подключаемых паттернов будут установлены в списке параметров ZUP.
Кнопка Просмотр 5-точечного рисунка открывает панель для работы с 5-точечным образцом. При нажатии на нее открывается следующий экран с графиком:
Обратите внимание, что изображение с шаблоном паттерна отображается на языке MQL4. Координаты точек паттерна XABCD используют время условных баров на графике. Время, которое можно установить, ограничено примерно 2033. Поэтому не рекомендуется максимально сжимать график на таймфрейме MN при работе с этим элементом пользовательского интерфейса.Время условных баров, к которым «привязаны» паттерны, может стать больше 2033 при сжатии графика. Это вызывает ошибку. Когда диаграмма сжимается до максимума, шаблон паттерна либо искажается, либо вообще не отображается.
Что можно сделать с получившимся окном?
Line дублирует / заменяет значение параметра SelectPattern, который устанавливает группы 5-точечных шаблонов для поиска.
При работе с графическим интерфейсом используются значения параметров, заданные через этот интерфейс.Если графический интерфейс отключен ExtPanel = false, используются значения, заданные на вкладке редактирования параметров индикатора. В этом случае на каждом графике доступны индивидуальные параметры.
Бычья кнопка в строке устанавливает отображение изображения с бычьей или медвежьей интерпретацией шаблона паттерна (по умолчанию бычья интерпретация отображается первой) и название отображаемого паттерна.
Строка соответствует параметру visiblePattern, который задает список паттернов, подключенных к поиску.
Каждая позиция в этой строке соответствует одному из 33 встроенных шаблонов ZUP. Если 1 установлено в позиции выбранного шаблона, это означает, что шаблон добавлен в поиск. 0 означает, что шаблон не используется.
Список шаблонов, добавленных в поиск, можно изменить несколькими способами.
- Переместите курсор в выбранное положение и щелкните левой кнопкой мыши. Первый щелчок показывает картинку с шаблоном выкройки. Второй щелчок изменяет 1 на 0 или 0 на 1.
Использование строки.Цифры 1 из 33 показывают положение, в котором установлен розовый курсор. Курсор также показывает, какой узор выбран для манипуляции. Используйте стрелки, чтобы установить новое положение курсора. Да / Нет изменяет 1 на 0 или 0 на 1.
Кнопка «Скрыть» устанавливает для всех позиций значение 0, т.е. все шаблоны удаляются из поиска. Здесь следует отметить следующее. Вы можете добавить в поиск более 33 паттернов. Но в строке из единиц и нулей всего 33 позиции. Когда розовый курсор перемещается в крайнее левое положение и нажимается <<, отображаются предыдущие 33 шаблона.Когда вы перемещаете розовый курсор в крайнее правое (33-е) положение и щелкаете >>, отображаются следующие 33 шаблона.
Для отладки программы подключил файл примерно с 265 паттернами, которые были созданы одним из пользователей ZUP в более ранних версиях индикатора и использовались только для поиска. Ранее шаблоны создавались с помощью внешних программ, что позволяло создавать файлы в формате * .CSV. Это довольно сложная работа. Теперь шаблоны можно создавать, записывая их параметры в файл CSV.Но пользоваться графическим интерфейсом еще проще.
- Стрелки в строке позволяют через параметр SelectPattern выбрать группы шаблонов, заданные в коде ZUP, и подключить их к поиску. Но работа этого параметра зависит от того, подключены ли к поиску только шаблоны ZUP, или дополнительно используются шаблоны из внешнего файла. Стрелки в позволяют выбрать значение readFromFileListPatterns — «Шаблоны из ZUP /« Шаблоны из внешнего файла »/« Шаблоны из ZUP и из файла ».Этот параметр устанавливает место для хранения паттернов. С помощью стрелок в можно выбрать внешний файл с параметрами шаблонов. Эта строка показывает, что вы можете соединить файл 1 из двух 1/2, который называется M. Это файл с параметрами паттернов Меррилла.
Кнопка New позволяет создать новый узор. Если подключены паттерны из внешнего файла, в зависимости от значения, выбранного в строке, могут появиться кнопки «Редактировать» и «Удалить». Если внешних файлов нет, кнопка «Редактировать» может появиться для встроенных шаблонов ZUP.Эта опция позволяет создавать собственные паттерны на основе доступных 33 паттернов, редактируя их параметры.
Ниже вы можете дополнительно увидеть строку или несколько строк со значениями дополнительных параметров, которые характерны для узора на правом изображении.
Щелчок по New открывает список из 8 строк с параметрами, которые могут быть установлены для 5-точечных шаблонов.
Повторный щелчок по New возвращает предыдущее экранное значение. Действие любых кнопок в ZUP GUI можно отменить повторным щелчком по той же кнопке или нажатием ESC.
При нажатии на одну из строк со списком параметров открывается следующее окно:
В данном случае была нажата пятая строка. На изображении показан пример узора, который можно создать, используя выбранные параметры. Значения исходных параметров шаблона используются для значений по умолчанию параметров этого нового шаблона. Параметры можно изменить. В шутку, на основе этой бабы-яги был создан новый паттерн:
Повторный щелчок по пятой строке показывает следующее:
Строка показывает редактируемые параметры.
Строка показывает выбранное значение параметра. Новое значение параметра выбирается с помощью стрелок. Его можно отредактировать вручную, щелкнув 0,382 и отредактировав значение параметра. Когда значение параметра изменяется, графическое представление шаблона также изменяется.
Кнопка Далее устанавливает выбранное значение и позволяет вам установить значение следующего параметра.
Количество еще не установленных параметров в строке уменьшается, и появляется следующий элемент шаблона BC.
После того, как первое значение параметра зафиксировано нажатием кнопки «Далее», появляется кнопка «Назад», позволяющая отменить изменения и отредактировать предыдущие значения параметров.
Две кнопки позволяют в любой момент подключить следующие параметры: линейный фильтр XB и соотношение длин крыльев шаблона. Соотношение устанавливается стрелками. Щелчок по значению, выбранному с помощью стрелок, позволяет вручную установить собственный коэффициент. ВНИМАНИЕ! Установите 0, чтобы отключить соотношение.
После того, как вы закончите редактировать параметры нового паттерна, вам будет предложено указать его имя:
Назовем его, например, AA.
После этого вам будет предложено выбрать имя файла для сохранения созданного рисунка. По умолчанию выбран файл, подключенный как внешний файл с шаблонами. Имя файла можно редактировать; в этом случае узор будет сохранен в файл с отредактированным именем. Если такой файл уже был создан, шаблон будет добавлен в конец списка. Если файла с таким именем не существует, будет создан новый файл.
Редактирование параметров шаблона аналогично созданию нового параметра.По окончании редактирования вам будет предложено сохранить полученный узор вместо отредактированного или сохранить его как новый узор в указанном файле * .csv. Если вы редактировали паттерн из встроенного списка ZUP, вам будет предложено сохранить паттерн как новый в выбранном файле.
файлов * .csv сохраняются в MQL4 \ Files \ ZUP \ ListPatterns.
Подробное описание некоторых кнопок я опускаю. Их значение ясно из приведенного выше описания.
Максимально допустимое значение может отображаться для некоторых параметров, которые вы создаете / редактируете.Позже изменить это значение будет невозможно. Это сделано для того, чтобы избежать установки таких значений параметров, которые сделают шаблон бессмысленным с выбранным ExtDeltaGartley и с уже установленными значениями параметров. То есть паттернов с такими значениями на графике не найти никогда. Появится кнопка «Игнорировать». Он позволяет задавать любые значения для параметра: позже нам может потребоваться увеличить значение ExtDeltaGartley, после чего недопустимые на данный момент значения станут действительными.
Часть вторая. Параметры поиска паттернов Гартли
Поиск паттернов Гартли включается параметром ExtIndicator = 11. Для поиска сканируется интервал графика баров ExtMaxBar. Это первый вариант поиска. Он называется «Поиск лекал с помощью сканера».
Поиск также может выполняться с другими значениями ExtIndicator. В этом случае параметр ExtGartleyOnOff включен и поиск выполняется по одному зигзагу, заданному параметром ExtIndicator.Это второй вариант поиска: «Поиск паттернов по зигзагу».
При переключении на другой таймфрейм паттерны, найденные с использованием первых двух опций, будут удалены с графика и будет выполнен новый поиск.
Есть третий вариант поиска закономерностей. Этот вариант описан в статье «ZUP — Универсальный зигзаг с паттернами Песавенто. Графический интерфейс»
Паттерны, отображаемые на графике с использованием третьего варианта, сохраняются при переключении на другие таймфреймы.Однако фрактальный фильтр может отключать их отображение на некоторых таймфреймах.
Шаблоны, созданные с помощью графического интерфейса, можно использовать во всех трех вариантах поиска.
Ниже представлен полный список параметров, используемых при поиске паттернов Гартли и при работе с графическим интерфейсом, описанным в первой части статьи.
- AlgorithmSearchPatterns — выбор алгоритма сканера для поиска паттернов для ExtIndicator = 11:
- 0 — соответствует ExtIndicator = 0 — стандартному ZigZag
- 1 — соответствует ExtIndicator = 1 — Alex ZigZag, размер луча задается в баллов
- 2 — соответствует ExtIndicator = 1 — Alex ZigZag, размер луча установлен в%
- 3 — соответствует ExtIndicator = 2
- 4 — соответствует ExtIndicator = 4
- 5 — соответствует ExtIndicator = 5
- 6 — соответствует ExtIndicator = 12
- PotencialsLevels_retXD — позволяет отображать уровни ретрейсмента XD потенциальных пятиточечных паттернов.В случае ExtIndicator = 11 применяется только в случае обнаружения паттерна; дальнейшие уровни отображаются от его точки C:
- 0 — отключить вывод потенциальных уровней
- 1 — отображать потенциальные уровни вместе с паттернами, если ExtGartleyOnOff = true
- 2 — отображать потенциальные уровни. Выкройки отключены.
- visibleLevelsABCD — установить способ отображения потенциальной точки D потенциальных пятиточечных паттернов:
- 0 — дополнительные уровни не отображаются
- 1 — отображать все варианты уровней восстановления BD
- 2 — отображать все уровни различных вариантов AB = CD
- 3 — отображать уровни восстановления BD и параметры AB = CD вместе
- maxDepth — максимальное значение глубины (minBars), до которого можно изменить глубину зигзага при активном поиске Паттерны Гартли.Применяется, если AlgorithmSearchPatterns = 0.
- minDepth — установить минимальное значение глубины для поиска паттернов Гартли.
- FiboStep — включить следующий расчет Backstep при поиске паттернов: Backstep = Depth * 1.618.
- IterationStepDepth — Шаг изменения параметра зигзага глубины при поиске паттернов Гартли.
- maxSize_ — максимальный размер луча в пунктах. Он используется при сканировании шаблонов, если AlgorithmSearchPatterns = 1, AlgorithmSearchPatterns = 3, AlgorithmSearchPatterns = 4, AlgorithmSearchPatterns = 6.
- minSize_ — минимальное значение луча в пунктах.
- IterationStepSize — Шаг изменения параметра зигзага размера при поиске паттернов Гартли.
- maxPercent_ — максимальный процент для расчета Зигзага Alex. Используется при сканировании паттернов, если AlgorithmSearchPatterns = 2.
- minPercent_ — минимальный процент для расчета Зигзага Alex.
- IterationStepPercent — Шаг изменения параметра зигзага в процентах (%).
- DirectionOfSearchMaxMin — направление поиска паттернов:
- false — от minDepth до maxDepth;
- true — от maxDepth до minDepth;
- SelectPattern — выбор паттернов из пяти точек для поиска:
- 0 — поиск всех паттернов
- 1 — поиск только стандартных паттернов — Gartle, Butterfly, Bat, Crab, кроме ВСЕГО
- 2 — поиск обычные и нетрадиционные паттерны, кроме ИТОГО
- 3 — поиск экзотических паттернов и антипаттернов, кроме ИТОГО
- 4 — поиск только антипаттернов, кроме ИТОГО
- 5 — поиск всех паттернов, кроме ИТОГО
- 6 — поиск только ВСЕГО
- 7 — случайный выбор пятиточечных образов для поиска по visiblePattern
- 8 — отключение поиска пятиточечных образов
- «Gartley»;
- «Летучая мышь»;
- «Альтернативная летучая мышь»;
- «Бабочка»;
- «Краб»;
- «Глубокий краб»;
- «Леонардо»;
- «Акула»;
- «Сайфер»;
- «Нен ЗВЕЗДА»;
- «5-0»;
- «Гартли»;
- «Летучая мышь»;
- «Альтернативная летучая мышь»;
- «Бабочка»;
- «Краб»;
- «Глубокий краб»;
- «Леонардо»;
- «Акула»;
- «Шифр»;
- «Нен ЗВЕЗДА»;
- «А 5-0»;
- «Черный лебедь»;
- «Белый лебедь»;
- «Наварро 200»;
- «макс. Летучая мышь»;
- «Макс Гартли»;
- «бабочка макс»;
- «ИТОГО 1»;
- «ИТОГО 2»;
- «ИТОГО 3»;
- «ИТОГО 4»;
- «ИТОГО».
- visiblePattern — укажите, какие шаблоны следует искать. По умолчанию поиск по всем шаблонам отключен.
- NumberPattern — порядковый номер шаблона, используемого для калибровки Зигзага. Параметры шаблона отображаются через InfoTF. Если NumberPattern = 0, отображается зигзаг с параметрами, как в режиме ExtIndicator = 0.
- ExtGartleyTypeSearch — режим поиска паттернов:
- 0 — завершить поиск после первого обнаруженного паттерна
- 1 — отобразить все паттерны на участке, указанном maxBarToD.Поиск повторяется при каждом пересчете зигзага. Режим «Китайская игрушка 1»
- 2 — отображать все паттерны на отрезке, заданном параметром maxBarToD. Поиск выполняется только один раз. Режим «Китайская игрушка 2»
- ExtHiddenPP — режим отображения зигзага для ExtIndicator = 11:
- 0 — зигзаг не отображается. В виде точек отображаются только крайние точки зигзага. Никаких паттернов Песавенто.
- 1 — отобразить зигзаг, откалиброванный по шаблону, заданному NumberPattern.Паттерны Песавенто отображаются обычным образом.
- 2 — Зигзаг не отображается. В виде точек отображаются только крайние точки зигзага. Паттерны Песавенто отображаются только для паттернов Гартли.
- ExtGartleyOnOff — отображать паттерны Гартли. Не в режиме сканера.
- maxBarToD — установить максимальное количество баров от нулевой точки до точки D паттерна.
- patternInfluence:
- 0 — отображать паттерны, содержащие не более чем maxBarToD баров от нулевого бара до бара точки D
- 1 — учитывать эффект паттерна, отменить эффект maxBarToD
- 2 — поиск паттернов выполняется выполняется по всей разметке зигзага
- pattern True = true — отображать паттерны, удовлетворяющие условию:
для медвежьих паттернов, от точки D не должно быть баров с максимумом, превышающим максимум точки D. до нулевого бара;
для бычьих паттернов, от точки D до нулевого бара не должно быть баров с минимумом, превышающим минимум рамки области развития точки D.
- AllowedBandPatternInfluence — установить соотношение расстояния между точками X и D узора. Это соотношение устанавливает расстояние от точки D до точки, где предположительно заканчивается влияние паттерна
- RangeForPointD — разрешить отображение области развития точки D
- OldNewRangeForPointD — выбрать метод построения построения области развития точки паттерна
- ExtColorRangeForPointD — цвет области развития точки D
- VectorOfAMirrorTrend = 1 отображать вектор тренда
- VectorOfAMirrorTrend = 2 отображать вектор зеркального тренда
- VectorOfAMirrorTrendColor — цвет линии обратного тренда
- VectorOfAMirrorTrendStyle — стиль линии обратного тренда
- shortNamePatterns — разрешить отображение имена паттернов
- visibleLineOrTriangle — разрешить отображение паттернов в виде линий или треугольников, кроме AB = CD паттернов
- PatternLineStyle — установить стиль линии для пятиточечных паттернов и AB = CD
- PatternLineWidth — установить ширину линии для пятиточечных паттернов и AB = CD
- ExtColorPatternsBullish — цвет бычьих паттернов
- ExtColorPatternsBearish — цвет медвежьих паттернов
- ExtColorPatternList — установить список цветов для заливки паттернов Гартли в режиме «Китайская игрушка».Названия цветов разделяются запятыми. Если в названии некоторых цветов есть ошибка, по умолчанию для них устанавливается красный цвет
- ExtDeltaGartley — допуск на отклонение цены для поиска паттернов, значения по умолчанию 9% — 0,09
- ExtDeltaGartleyPRZ — специальный допуск для построения рамка развития точки D паттерна
- levelD — отображение уровней ретрейсментов XD возможных точных версий паттернов для текущей комбинации
- colorLevelD — установка цветов уровней ретрейсментов XD
- Equilibrium — отображение линий Equilibrium, Reaction1 и Reaction2
- ReactionType — установите тип линии реакции
- EquilibriumStyle — установить стиль линии
- EquilibriumWidth — установить ширину линии
- ColorEquilibrium — установить цвет Equilibrium
- ColorReaction — установить цвет Reaction1 и Reaction2
- Ext_3Drives — отобразить шаблон 3 Drives
- Ext_xO — установить соотношение для поиск в 3-х дисках, 7 точек ern
- Дракон — отображение паттерна Дракона
- PeakZZDragon — установка порядкового номера крайней точки зигзага, до которого будет выполняться поиск паттерна Дракон
- Ext_4PointPattern — разрешить поиск паттерна продолжения из 4 точек
- _maxXB — установить максимальное значение ретрейсмента XB для 4-точечного паттерна.Узнайте больше о шаблоне здесь: http://kanetrading.com/
- ABCD — включить поиск шаблона AB = CD:
- 0 — скрыть шаблоны AB = CD
- 1 — отобразить любой AB = CD
- 2 — отображать только гармонику AB = CD с соотношениями, соответствующими серии Фибо в пределах допуска
- searchABCDAlternate — отображать альтернативные шаблоны AB = CD
- ABCDAlternate — установить список альтернативных шаблонов AB = CD. Отношения X из уравнения X * AB = CD перечислены там через запятую
- visibleABCDrayZZ — отобразить паттерны AB = CD в виде линии
- Ext_noname — разрешить поиск неизвестных паттернов из пяти точек со всеми четырьмя ретрейсментами, равными одному из Фибоначчи
- CustomPattern — отображение пользовательских шаблонов:
- 0 — скрытие пользовательских шаблонов
- 1 — отображение вместе с другими шаблонами
- 2 — отображение только пользовательских шаблонов
- NameCustomPattern — имя пользовательского шаблона
- minXB — установка минимальное значение восстановления XB
- maxXB — установить максимальное значение восстановления XB
- minAC — установить минимальное значение восстановления AC
- maxAC — установить максимальное значение восстановления AC
- minBD — установить минимальное значение восстановления BD
- maxBD — установить максимальное значение ретрейсмента BD
- minXD — установить минимальное значение ретрейсмента XD
- maxXD — установить t Максимальное равновесное значение ретрейсмента XD.
Retracement High и Low задает диапазон поиска.
- filterEquilibrium — включает фильтрующую линию, проходящую через точки шаблона X и B. Если фильтр включен, паттерн отображается, когда цена пробивает линию при движении от C к D. Работает только с пользовательскими и безымянными паттернами.
- readFromFileListPatterns — установить чтение списка паттернов из файла \\ ZUP \ ListPatterns \ listpatterns.csv:
- 0 — запретить чтение списка паттернов из файла
- 1 — использовать при поиске пятиточечных паттернов только те паттерны, которые находятся в списке, загруженном из файла
- 2 — добавить список паттернов из файла в список пятиточечных паттернов, встроенный в ZUP.В этом случае формируется составной список шаблонов.
Файлы * .csv находятся в MQL4 \ Files \ ZUP \ ListPatterns.
- NameFileListPatterns — задайте имя файла csv, из которого будет читаться список параметров шаблона
- writeToFileListPatterns — разрешить запись списка пятиточечных шаблонов:
- 0 — записать в \\ ZUP \ ListPatterns \ listpatternsdefault. csv
- 1 — запись в \\ ZUP \ ListPatterns \ listpatternscustom.csv
- 2 — запись в \\ ZUP \ ListPatterns \ listpatternsmixt.csv
- picture — отправить скриншот графика с паттерном в файл
Файлы со скриншотами найденных паттернов сохраняются в MQL4 \ Files \ ZUP \ PicturePatterns.
- writeInfoPatternsToFileXML — отправить параметры текущего пятиточечного шаблона в файл XML:
- 0 — отключить отправку параметров в файл
- 1 — временные параметры отправляются в развернутом виде
- 2 — временные параметры отправлено за количество секунд
Файл *.xml файлы с параметрами найденного паттерна сохраняются в MQL4 \ Files \ ZUP \ XML.
- writeInfoPatternsToFileCSV — отправить параметры текущего пятиточечного шаблона в файл CSV:
- 0 — отключить отправку параметров в файл
- 1 — временные параметры отправляются в развернутом виде
- 2 — временные параметры указаны отправлено за количество секунд
Файлы * .csv с параметрами найденного паттерна сохраняются в MQL4 \ Files \ ZUP \ CSV.
- namefileSymbolPeriod = true — установить имена файлов с изображениями шаблонов и параметрами Symbol () + «_» + Period () + «_ Patterns
- InfoPointD — отображать данные о точке D шаблона крупным шрифтом
- MonitorPatterns — включить монитор шаблонов
- TextSize — установить размер шрифта в мониторе шаблонов
- ExtGlobalVariableSet — включить запись данных о шаблонах в глобальные переменные терминала
Информация о найденном шаблоне может быть выведена в глобальную переменную с именем «ZUP» + _Symbol + _Period.Пример имени глобальной переменной: ZUPGBPUSD240. Если образец найден, в переменную будет записана цифра 1.
Объяснение некоторых функций ZUP, реализованных в режимах поиска паттернов Гартли
Монитор паттернов
Работа монитора паттернов демонстрируется ниже на примере режима «Китайская игрушка». В этом режиме на графике отображается множество найденных паттернов:
Монитор — это линии в верхнем левом углу графика.Каждая линия соответствует одному из паттернов, отображаемых на графике. Цвет первых трех столбцов соответствует цвету соответствующего шаблона. Цвет четвертого столбца: синий означает бычий паттерн, заданный параметром ExtColorPatternsBullish, красный означает медвежий паттерн, заданный параметром ExtColorPatternsBearish.
Первый столбец содержит номер бара, на котором находится точка D.
Во втором столбце отображаются параметры minBars / ExtBackstep зигзага, на котором находится соответствующий паттерн.
В третьем столбце показано условное отклонение ретрейсментов XC-XB-AD-CD от идеального значения. Давайте подробнее рассмотрим конкретный пример паттерна «Бычья бабочка» [1.414 / .786 / .786 / 2.0] в пятой строке монитора паттернов. Идеальные значения ретрейсмента показаны в квадратных скобках после названия паттерна. Как образуются условные отклонения? Что означают условные отклонения?
Чем больше число, тем больше отклонение от идеального значения.
- Значение 0: отклонение должно быть меньше значения параметра ExtDeltaGartleyPRZ. Значение параметра по умолчанию — 2%.
- Значение 1: отклонение должно быть меньше значения параметра ExtDelta. Значение по умолчанию — 4%.
- Значение 2: отклонение должно быть меньше значения параметра ExtDeltaGartley. Значение по умолчанию — 9%.
- Значение *: отклонение больше, чем указанное в значении 2. Найденный шаблон будет соответствовать шаблону, который был бы найден в первых версиях ZUP.
Линия равновесия и линия вектора зеркального тренда
Параметр Equilibrium позволяет отображать линию равновесия, которая проходит через точки XB модели и две линии реакции (красные пунктирные линии):
Реакция линия 1 параллельна линии равновесия. Расстояние между этими линиями равно расстоянию между точкой C шаблона и линией равновесия.
Линия реакции 2 параллельна линии равновесия.Расстояние между этими линиями равно расстоянию между точкой А рисунка и линией равновесия.
Когда цена приближается к линии реакции, можно ожидать либо коррекции, либо окончания формирования паттерна.
Вектор зеркального тренда включается параметром VectorOfAMirrorTrend. После этого начинается рисование пунктирной линии. Линия вектора зеркального тренда на изображении выше бледно-зеленая. Он проводится через диагональ потенциальной зоны разворота, которая показана в виде красного прямоугольника в точке D фигуры.
Часть третья. Кратко о других паттернах
Помимо паттерна Гартли, ZUP позволяет работать с паттернами Песавенто и другими типами паттернов.
К одному из таких типов относятся паттерны Меррилла. Они используются в сочетании с полосами Боллинджера. ZUP позволяет идентифицировать такие паттерны на уже сформированном Зигзаге. Паттерны не отображаются на графике, а отображаются только их названия. Динамические паттерны Меррилла формируются на первых четырех лучах зигзага справа.Узоры на 2-5 лучах статичны.
Информация о паттернах Меррилла включается с помощью параметра infoMerrillPattern = true. Информация о паттерне отображается мелким шрифтом в верхнем левом углу графика. Имя шаблона можно отобразить крупным шрифтом, установив bigText = true. Такая большая метка отображается в правом верхнем углу.
На первых четырех лучах сформировался динамический паттерн Меррилла под названием Треугольник.
Статический узор под названием M13 сформировался на лучах со второго по пятый.
Паттерны Меррилла состоят из пяти точек. Их графическое представление может быть создано с помощью графического интерфейса. Например, это уже сделал участник форума Станислав Тривайло .
Если bigText = true, информация о найденном паттерне Гартли также может отображаться крупным шрифтом. Эта информация и монитор могут отображаться только для первых двух вариантов поиска по шаблону.
Выводы
Это краткое описание поможет вам понять, как использовать ZUP для поиска шаблонов.
Вы можете скачать платформу индикаторов ZUP в Маркете: https://www.mql5.com/ru/market/product/19758
.
Архивы поиска шаблонов — GeeksforGeeks
Учитывая четыре целых числа N, M, A, B, где N — количество строк, а M — количество столбцов, задача состоит в том, чтобы… Подробнее »
Для двумерной сетки arr [] [] с разными символами задача состоит в том, чтобы определить, содержит ли она цикл или нет. Последовательность символов или… Подробнее »
Для строки S длины N и целого числа K найдите строку наименьшей длины, которая содержит строку S в качестве подстроки точно… Подробнее »
Для массива arr [], состоящего из N элементов, задача состоит в том, чтобы проверить, можно ли отсортировать данный массив, выбирая только угловые элементы… Подробнее »
Даны две строки S1 и S2.Задача состоит в том, чтобы обернуть каждый экземпляр строки S2 в строку S1, с любой строкой с обеих сторон.… Подробнее »
Учитывая большое число в виде строки N, задача состоит в том, чтобы вставить дефис между двумя соседними нечетными цифрами данного числа… Подробнее »
Учитывая целое число N, представляющее размер матрицы, задача состоит в том, чтобы построить квадратную матрицу N * N, которая имеет элемент из… Подробнее »
Дано число N и любое число K для ряда, образованного как K, K + 1, K + 2, K + 3, K… Подробнее »
Дано число N и массив arr [], которые состоят из слияния последовательности различных целых чисел длины N любое количество раз с сохранением относительного… Подробнее »
Учитывая четное целое число N, задача состоит в том, чтобы построить строку так, чтобы общее количество различных подстрок этой строки, которые… Подробнее »
Учитывая четыре целых числа N, M, X и Y, задача состоит в том, чтобы построить матрицу N * M так, чтобы каждая ячейка состояла из… Подробнее »
Для массива A [], состоящего из N различных целых чисел, задача состоит в том, чтобы переставить данный массив так, чтобы сумма всех непустых значений с одинаковым индексом… Подробнее »
Учитывая двоичный массив arr [] cof размером N, задача состоит в том, чтобы уменьшить массив до одного элемента с помощью следующих двух операций: A… Подробнее »
Учитывая число N, задача состоит в том, чтобы определить, можно ли составить треугольник Паскаля с полным слоем, используя общее число… Подробнее »
Для строки S задача состоит в том, чтобы изменить идентификатор строки, который не соответствует ни одному из правил, приведенных ниже, и распечатать обновленный… Подробнее »
,
Design for Discovery, Питер Морвилл
Что говорят люди о шаблонах поиска
« Шаблоны поиска приятно читать — очень вдумчивый и наводящий на размышления. Это наиболее исчерпывающий обзор разработки эффективных поисковых систем I ‘ видел.» — Ирин Ау, директор по взаимодействию с пользователем, Google
«Мне нравится эта книга! Благодаря Питеру и Джеффри я теперь знаю, что поисковый запрос (да, старый скучный мерзавец, которому не все равно)
Что люди говорят о поиске Шаблоны
« Шаблоны поиска приятно читать — они очень содержательные и наводящие на размышления.Это самый исчерпывающий обзор создания эффективных поисковых систем, который я когда-либо видел ». — Ирэн Ау, директор по взаимодействию с пользователями, Google
« Мне нравится эта книга! Благодаря Питеру и Джеффри я теперь знаю, что поиск (да, старый скучный мерзавец, которому небезразличен поиск) — один из самых крутых способов взглянуть на мир », — Дэн Роам, автор, The Back of the Napkin ( Портфолио в твердом переплете)
« Шаблоны поиска — это увлекательное руководство по практическим вопросам разработки интерфейса поиска.Он содержит огромное количество снимков экрана и иллюстраций, которые отражают лучшие современные методы проектирования и представляют свежий взгляд на более широкую роль поиска и открытий ». — Марти Херст, профессор Калифорнийского университета в Беркли и автор, Search User Interfaces (Кембридж University Press)
«Я не часто встречаю книгу, в которой задаются глубокие вопросы о фундаментальной деятельности человека, а затем я перехожу к ответам на эти вопросы с помощью практических наблюдений и предложений. Шаблоны поиска — это экспедиция в самое сердце Интернета и человеческого познания, и для меня это было восхитительное путешествие, которое принесло множество идей ». — Дэйв Грей, основатель и председатель XPLANE
« Поиск быстро меняет все мы знаем, но люди не понимают, как mavens разрабатывают поиск: складывая панировочные сухари, ароматизируя виджеты и не отрывая глаз от движка. Я настоятельно призываю вас обратить ваше внимание на эту уникальную и важную книгу ». — Брюс Стерлинг, писатель, футурист и соучредитель, The Electronic Frontier Foundation
« Как человек, который много ищет (и часто заканчивается разочарованием), Шаблоны поиска — это открытие.»- Найджел Холмс, дизайнер, теоретик и директор, Explanation Graphics
» Search Patterns — потрясающая книга, которую необходимо иметь! Внутри вы узнаете, почему и где практически все уловки и методы современного дизайна поиска ». — Джаред Спул, генеральный директор и основатель, разработка пользовательского интерфейса
Поиск — одно из самых разрушительных нововведений нашего времени. Он влияет на то, что мы покупайте и куда мы идем. Он определяет то, как мы учимся и во что мы верим. В этой провокационной и вдохновляющей книге вы исследуете шаблоны проектирования, применимые в различных категориях: Интернет, электронная коммерция, предприятие, настольные компьютеры, мобильные устройства, социальные сети и реальные поиск и открытие времени. Search Patterns , наполненный красочными иллюстрациями и примерами, воплощает в жизнь современный поиск информации, охватывающий такие разнообразные темы, как актуальность, фасетная навигация, мультитач, персонализация, визуализация, мультисенсорный поиск и дополненная реальность.
Основываясь на собственном опыте, а также на передовых методах и исследованиях, основанных на фактах, авторы не только предлагают практическое руководство, которое поможет вам создавать эффективные поисковые приложения, но и побуждают вас представить будущее открытий.Вы найдете Search Patterns интригующим и бесценным, независимо от того, являетесь ли вы веб-практиком, мобильным дизайнером, предпринимателем в области поиска или просто интересуетесь этой темой.
Откройте для себя язык шаблонов для поиска, который охватывает психологию и поведение пользователя, информационную архитектуру, дизайн взаимодействия и новые технологии
Повышение эффективности предприятия и продаж электронной коммерции
Позволяет мобильным пользователям достигать целей, выполнять задачи и находить то, что им нужно
Стимулируйте инновации в дизайне поисковых интерфейсов и приложений
.
