Основные гипотезы:
1) гипотеза
плоских сечений:
поперечное сечение стержня плоское и
перпендикулярное геометрической оси
до деформации остаётся плоским и
перпендикулярным геометрической оси
в процессе деформации;
2) гипотеза
постоянства расстояний между поперечными
сечениями:
расстояния между поперечными сечениями
стержня при кручении не изменяются;
3) гипотеза
о прямолинейности радиусов в поперечном
сечении:
радиусы, проведённые в поперечных
сечениях, остаются прямыми в процессе
деформации.
Эпюры распределения касательных напряжений

ρ — полярная координата
τρ
— касательное
напряжение
Mk
— крутящий
момент
Ip — полярный момент инерции
В формуле τ зависит
от ρ, следовательно, эпюра должна
описываться прямой линией.
Касательные напряжения
распределены по плоскости всего сечения,
поэтому можно построить эпюру τ на любом
произвольно проведенном радиусе. Формулу
для определения касательных напряжений.
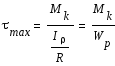
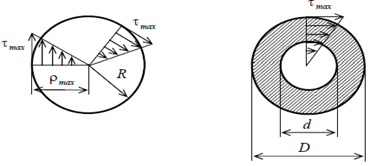
Учитывая характер
распределения касательных напряжений
по ширине поперечному сечению, можно
сделать вывод о том, что по мере приближения
к центру тяжести поперечного сечения
касательные напряжения уменьшаются, а
в центре тяжести равны нулю.
3.Определение угла закручивания при кручении. Жесткость при кручении. Главные напряжения и главные площадки. Закон Гука при кручении.

Условие жесткости
обычно формулируется исходя из
максимального угла закручивания,
приходящегося на 1 погонный метр.
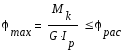
Где φ расчетное —
задаваемая техническими условиями
величина угла закручивания
Главные площадки
– это площадки, проходящие через
исследуемую точку, на которых Касательные
напряжения отсутствуют.
Главные напряжения
– это возникающие на главных площадках
нормальные напряжения
В общем случае нагружения
(при объемном напряженном состоянии)
среди множества площадок, проходящих
через некоторую точку тела, всегда можно
найти три взаимно перпендикулярные
главные площадки. В окрестности любой
точки деформированного твердого тела
всегда можно выделить элементарный
параллелепипед, ориентированный в
пространстве таким образом, что по его
граням будут возникать только нормальные
(главные) напряжения
Индексы расставляются
после вычисления главных напряжений.
Должно выполняться неравенство:
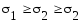
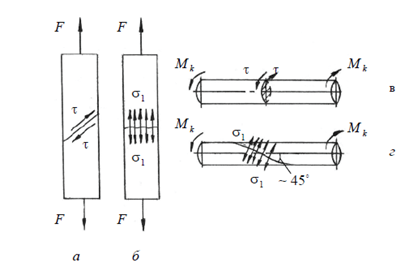
4. Особенности разрушения пластичных и хрупких материалов при растяжении и кручении.
Пластичные материалы
разрушаются «путём сдвига», поэтому
при растяжении плоскость разрушения
располагается под углом 45° (а) по отношению
к оси нагружения там, где действуют
наибольшие касательные напряжения. При
кручении пластичных материалов разрушение
происходит по плоскости перпендикулярной
геометрической оси бруса (в). Хрупкие
материалы разрушаются «путём отрыва»,
при растяжении поверхность разрушения
располагается перпендикулярно оси
растяжения, т.е. линиям действия наибольших
нормальных напряжений, а при кручении
под углом 45° (б и г).
5. Статически неопределимые задачи при кручении.
Задачу, в которой для
определения опорных реакций и внутренних
усилий требуется кроме уравнения
равновесия привлекать условия деформации,
называется Статически неопределимой
Решение: мысленно
нужно раскрепить стержень, отбросив
жесткую заделку. Разбить стержень на
участки. Определить угол закручивания,
как сумма углов закручивания на этих
участках. Используя метод сечений,
можно определить крутящие моменты на
участках как алгебраическая сумма
крутящих моментов, действующих по одну
сторону от рассматриваемого сечения.
Значения углов поворота определяем по
формуле Гука.
Если сумма углов
поворота = 0, то решение правильное.
1.2. Гипотезы и допущения, принятые в сопротивлении материалов
1.2. ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ 1. Гипотеза сплошности и однородности — материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела. Атомистическая теория дискретного строения вещества во внимание не принимается. Гипотеза позволяет не учитывать особенности кристаллической структуры металла, разный химический состав и прочностные свойства связующего и наполнителей в пластмассах, бетонах (щебень, песок, цемент), наличие сучков в древесине. 2. Гипотеза об изотропности материала – физико-механические свойства материала одинаковы по всем направлениям. В некоторых случаях предположение об изотропии неприемлемо, материал является анизотропным. Так, анизотропными являются древесина, свойства которой вдоль и поперек волокон различны, а также армированные (композиционные) материалы. 3. Гипотеза об идеальной упругости материала – тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию. 4. Гипотеза о совершенной упругости материала – перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения (справедлив закон Гука). В действительности реальные тела можно считать упругими только до определенных величин нагрузок, и это необходимо учитывать, применяя формулы сопротивления материалов. 5. Гипотеза Бернулли о плоских сечениях – поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси в деформированном состоянии; при изгибе сечения поворачиваются не искривляясь. 6. Принцип Сен-Венана – в сечениях, достаточно удаленных от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки. Резко выраженная неравномерность распределения напряжений по сечению 2-2, показанная на рисунке, постепенно выравнивается (сечение 3-3) и на удалении, равном ширине сечения (сечения 4-4 и 5-5), исчезает. 7. Принцип Д’Аламбера – если к активным силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил. Принцип используется в расчетах на прочность при динамическом действии сил. 8. Принцип независимости действия сил (принцип суперпозиции) – результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательности их приложения. Это же справедливо и в отношении деформаций. 9. Принцип начальных размеров (гипотеза о малости деформаций) – деформации в точках тела настолько малы по сравнению с размерами деформируемого тела, что не оказывают существенного влияния на Рис. 1.1. Распределение нормальных напряжений в поперечных сечениях стержня при растяжении сосредоточенной силой А – площадь поперечного сечения взаимное расположение нагрузок, приложенных к телу. Допущение применяют при составлении условий статики, считая тело абсолютно твердым. 10. Допущение об отсутствии начальных внутренних усилий в теле до приложения нагрузки. Почти во всех реальных деталях и элементах конструкций указанное допущение полностью не выполняется. Внутренние напряжения возникают в деревянных конструкциях вследствие не- равномерного высыхания; в стальных и чугунных отливках – вследствие неравномерного охлаждения; в стальных деталях – вследствие термической (закалка…) и механической (шлифование…) обработок. Формирование колесных пар для железнодорожных вагонов осуществляют путем за- прессовки колес на ось. За счет натяга создаются напряжения в ступице колеса и подступичной части оси. Замечание о точности расчетов и округлении результатов. С учетом изложенных гипотез и допущений, а также разбросов результатов экспериментов по определению механических свойств, точность инженерных расчетов не превышает 3–5 %. В некоторых случаях погрешность 10–15 % считают приемлемой. На практике, если нет специальных указаний, результат округляют до трех значащих цифр. Например, результат 568 234 следует округлить до 568 000, а результат 0,00237648 – до 0,00238 или 2,38•10-3.
Основные гипотезы и принципы сопротивления материалов — Студопедия
1. Гипотеза о сплошности материала. Предполагается, что вещество непрерывно распределено по всему объему, занимаемому телом. Это противоречит атомно-молекулярному строению тел, но несущественно для макрообъектов и позволяет применять математический аппарат, разработанный для непрерывных функций.
2. Гипотеза об однородности. Считается, что в любой точке тела механические свойства одинаковы.
3. Гипотеза об изотропности. Механические свойства материала в каждой точке по любому направлению одинаковы.
4. Гипотеза о малости деформаций. Предполагается, что рассматриваемые материалы настолько жестки, что при действии эксплуатационных нагрузок их относительные деформации малы по сравнению с единицей.
5. Гипотеза об идеальной упругости. Упругими называются деформации, исчезающие после устранения вызвавшей их нагрузки.Таким образом, после разгрузки идеально-упругого тела все деформации исчезают.
6. Гипотеза о линейной зависимости между деформациями и механическими напряжениями, т.е. считается, что материал подчиняется закону Гука.
Плоский изгиб. Деформации и нормальные напряжения при чистом изгибе.
Изгиб называется плоским, если плоскость действия изгибающей нагрузки проходит через главную центральную ось инерции сечения.
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы Qy изгиб называется поперечным.
В поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия.
σ = Еy / ρ, где E – модуль упругости, ρ — радиус кривизны нейтрального слоя (Напряжения в нейтральном слое равны нулю). Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Плоский изгиб. Касательные напряжения при изгибе.
Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И. Журавский, который в 1855 году предложил следующую формулу: τ = QS / (I d), где Q-поперечная сила, S-статический момент относит. центр. оси части сечения, I-момент инерции всего сечения, b-ширина.
Гипотезы сопромата
Для построения теории сопротивления материалов принимают ряд гипотез о структуре и свойствах материалов, а также о характере деформации.
1. Гипотеза о сплошности материала. Предполагается, что материал полностью заполняет занимаемый им объем. Атомистическая теория дискретного строения вещества во внимание не принимается.
2. Гипотеза об однородности и изотропности. Предполагается, что свойства материала одинаковы во всех точках и в каждой точке — во всех направлениях. В некоторых случаях предположение об изотропии материала неприемлемо. Так, анизотропными являются древесина, свойства которой вдоль и поперек волокон существенно различны, а также армированные материалы или так называемые композиционные материалы.
3. Гипотеза о малости деформации (гипотеза относительной жесткости материала). Предполагается, что деформации малы по сравнению с размерами деформируемого тела. На этом основании пренебрегают изменениями в расположении внешних сил относительно отдельных частей тела при деформации и уравнения статики составляют для недеформированного тела. В некоторых случаях от этого принципа приходится отступать, что оговаривается особо.
4. Гипотеза о совершенной упругости материала. Все тела предполагаются абсолютно упругими. В действительности реальные тела можно считать упругими только до определенных величин нагрузок, и это необходимо учитывать, применяя формулы сопротивления материалов,
5. Гипотеза о линейной зависимости между деформациями и нагрузками. Предполагается, что для большинства материалов справедлив закон Гука, устанавливающий прямо пропорциональную зависимость между деформациями и нагрузками.
Как следствие гипотез о малости деформаций и о линейной зависимости между деформациями и усилиями при решении большинства задач сопротивления материалов применим принцип суперпозиции (принцип независимости действия и сложения сил). Например, усилия в любом элементе конструкции, вызванные различными факторами (несколькими силами, температурными воздействиями), равны сумме усилив, вызванных каждым из этих факторов, и не зависят от порядка их приложения. Это же справедливо и в отношении деформаций.
6. Гипотеза плоских сечений. Предполагается, что мысленно проведенные плоские сечения, перпендикулярные к оси стержня, в процессе его деформирования остаются плоскими и перпендикулярными к оси.
Эти, а также некоторые другие гипотезы позволяют решать широкий круг задач по расчету на прочность, жесткость и устойчивость, результаты таких расчетов обычно хорошо согласуются с данными эксперимента.
Гипотезы сопротивления материалов | Сопромат это легко!
Гипотеза об однородности и сплошности материала
а) допущение об однородности и непрерывности материала, т. е. принимают, что свойства материала не зависят от формы и размеров тела и одинаковы во всех его точках; Сплошность материала также равномерна. Нет ни включений ни раковин ни «непроваров»
В реальной жизни все тела имеют дефекты и несплошности. Но чтобы иметь возможность рассчитывать элементы конструкции, сопротивление материалов, при выводе всех своих формул использует идеализацию объекта и говорит, что тело однородное и сплошное по всему объему.
б) допущение о малости рассматриваемых перемещений. Предполагают, что перемещения, возникающие в конструкции в результате ее деформации, настолько малы, что по сравнению с размерами элементов ими можно пренебречь;
Гипотеза о линейной зависимости между силами и перемещениями
в) допущение о линейной зависимости между силами, действующими на конструкцию, и вызываемыми ими перемещениями. Согласно этому допущению величины упругих перемещений, возникающих в конструкции, прямо пропорциональны величинам вызвавших их сил;
Пропорциональность между силой и изменением размера объекта сильно зависит от материала из которого он изготовлен. Так у стали хорошо заметна линия пропорциональности, на которой этот закон соблюдается. Более мягкие материалы имеют линию не прямую, а больше криволинейную форму. Но сопротивление материалов этими нюансами пренебрегает, и ведет пересчет на прямолинейную форму. От нее уже и отталкиваются в дальнейших расчетах.
Об идеальной упругости материала
г) допущение об идеальной упругости материала. Предполагают, что материал обладает способностью полностью восстанавливать первоначальные размеры и форму после устранения нагрузок. Это допущение справедливо при ограниченных нагрузках, выше которых в материале возникают остаточные деформации, не исчезающие после удаления нагрузки;
После приложения нагрузки, в зависимости от ее величины объект, тело может полностью восстановится и может восстанавливаться не на 100% (сейчас речь только об упругих деформациях). Так вот восстановление после снятия нагрузки в пределах упругих деформаций считается в сопротивлении материалов 100%, т.е. идеальным. Что конечно же в реальной жизни не наблюдается. Но это нужно для введения законов, которые позволили бы производить расчеты.
д) допущение, называемое принципом независимости действия сил. Согласно этому принципу, результат воздействия на сооружение системы нагрузок, приложенных одновременно, равен сумме результатов воздействия тех же нагрузок, прикладываемых к телу по отдельности.
Использование принципа независимости действия сил возможно при условии соблюдения допущений б и в;
е) допущение, именуемое гипотезой плоских сечений (Я. Бернулли), на основании которой предполагают, что плоские поперечные сечения, проведенные в брусе до деформации, остаются плоскими и нормальным, и к продольной оси и после деформации.
Напряжение, величина напряжения — что это
Напряжение в сопротивлении материалов это мера которая позволят оценить величину действия силы на единицу сопротивляемости этой силе, площади очень маленькой площадки, из которых складывается сопротивление всей площади елемента конструкции. При этом для разных материалов получены максимальные величины этих напряжений. Так называемые допустимые напряжения. Таким образом получив напряжение в элементе конструкции, при расчете, мы можем подобрать материал или ответить на сколько близок элемент к допустимому напряжению.
Величина напряжений в каждой точке является мерой внутренних сил, которые возникают в материале как результат деформации, вызванной внешней силой
Немного о нашем сайте:
Пройти курсы по сопротивлению материалов, получить короткие и емкие уроки для подготовки к экзамену студентам или инженеру вспомнить, улучшить уровень подготовки по отдельным темам? Это легко! С Александром Заболотным!
По цене и условиям обучения посмотрите ссылку.
Кроме обучения сопротивлению материалов предлагаю получить знания и навыки решения задач по строительной механике.
Видео канал со снятыми видео уроками по сопротивлению материалов и строительной механике вы найдете по следующей ссылке.
Список видео уроков последовательно один за другим, где я рассказываю о сопротивлении материалов вы найдете по следующей ссылке:
Приветственное видео канала, для того чтобы познакомиться и подписаться, чтобы не пропустить новые видео уроки предлагаю ниже:
Рубрики
Репетитор по сопромату, Сопромат онлайн
Метки
допущения в сопротивлении материалов, задачи курса сопротивление материалов, классический курс сопротивления материалов в решениях задач, курс сопромата для чайников, о предмете сопротивление материалов, основные гипотезы сопротивления материалов, сопромат гипотезы, сопромат допущения, сопромат репетитор, Сопротивление материалов, сопротивление материалов краткий курс, сопротивление материалов примеры решения задач
Проверка статистических гипотез — Электронный учебник K-tree
Что это и кому это нужно?
Проверка (тест) статистической гипотезы — это способ математического определения верности некоторого утверждения на основе
закона распределения. Освоив этот метод, Вы сможете делать математически обоснованные выводы, например:
Пример #1
Вы изготавливаете кубики для игры в кости и чтобы убедиться, что кубик отлично сбалансирован, Вы проводите тест — бросаете кости 600 раз
и решаете, что если каждое число выпало 100±10 раз, то кубик сбалансирован.
Пример #2
На производстве 5% продукции отбраковывается, Вы разработали новую технологию и хотите проверить, уменьшится ли
количество брака.
Основные термины, определения и формулы
Нулевая и альтернативная статистические гипотезы
Математически, условие статистического теста записывается в виде основной (нулевой) гипотезы H0 и
альтернативной (конкурирующей) гипотезы H1. Основная гипотеза подразумевает некое значение параметра.
Альтернативная гипотеза используется для обозначения области, которая нам также может быть интересна.
Теперь в примерах:
В первом примере мы хотим узнать, будет ли количество каждого выброшенного числа равно 100±10, при этом для нас
неудачным будет как больше 110 так и меньше 90
H0: μ = 100±10
H1: μ ≠ 100±10научная запись выглядит так:
H0: μ = 100
H1: μ ≠ 100
α = 0.1
Во втором примере мы хотим узнать, новая технология лучше старой? При этом нас не интересует, стала ли она хуже,
а только есть ли улучшения. Предположим, что если количество брака осталось на уровне 5±0.25%, то процесс не стал лучше,
если количество брака меньше 4.75%, то улучшения есть:
H0: p = 5±0.25%
H1: p < 4.75%научная запись выглядит так:
H0: p = 0.05
H1: p < 0.05
α = 0.05
Критическая область и две ошибки
Область значений, в которой основная гипотеза неверна — это критическая область, размер этой области задаётся в виде уровня значимости α:
Мы имеем значения от 100 до 200 и хотим проверить,
мы предполагаем, что в критической области основная гипотеза неверна, если наше предположение неверно — значит мы ошиблись, такая ошибка называется
ошибка первого рода. Для альтернативной гипотезы мы также можем допустить ошибку, такая ошибка будет называться ошибка второго рода
Почему?
Мы формулируем гипотезу так, что бы неверное отвержение основной гипотезы являлось для нашего решения более существенным,
чем неверное принятие альтернативной, вот пример:
Проводится исследование, есть ли связь между курением и заболеванием раком, основная гипотеза выдвигается такая: курение вызывает рак. Если мы
отвергнем это утверждение, а оно окажется верным — мы ставим под угрозу человеческие жизни (ошибка первого рода). При этом, если курение не вызывает рак,
а в ходе эксперимента мы утвердили, что вызывает, то особых последствий это не вызовет (ошибка второго рода).
В условиях принятия решения мы хотим контролировать уровень ошибки первого рода, т.е. если нам необходимо принять решение относительно некоего утверждения,
мы должны задаться некоторым уровнем значимости α и последующие расчёты будут зависеть от этого параметра.
Необходимо проверить,
Уровень значимости, статистическая мощность
Уровень значимости α — это вероятность допустить ошибку первого рода. Уровень значимости и ошибка первого рода — это одно и то же.
Статистическая мощность связана с ошибкой второго рода (β), статистическая мощность — это вероятность отвергнуть основную гипотезу, когда верна
альтернативная. Вероятность ошибки второго рода и статистическая мощность в сумме дают 100%, соответственно, чем больше статистическая мощность,
тем меньше вероятность допустить ошибку второго рода.
Итак, мы имеем:
Проверка статистической гипотезы — математическое представление некоего утверждения
Нулевая гипотеза (H0) — предположение о некоем параметре θ, H0: θ = θ0
Альтернативная гипотеза (H1) — предположение о некоем параметре θ, H1: θ = θ0
Критическая область — область, в которой основная гипотеза H0 неверна
Ошибка I рода — вероятность отвергнуть основную гипотезу, когда она верна
Ошибка II рода — вероятность принять основную гипотезу, когда она неверна
Пример
Математическая запись гипотезы, что среднее значение генеральной совокупности равно 2
H0 : μ = 2
H1 : μ ≠ 2
Ещё пример
Математическая запись гипотезы, что среднее значение выборки А и среднее значение выборки В равны
H0 : μA = μB
H1 : μA ≠ μB
Что бы уж точно
Математическая запись гипотезы, что среднее значение выборки А меньше среднего значения выборки В
H0 : μA < μB
H1 : μA ≥ μB
Уровень значимости α
Уровень значимости (его также можно было бы назвать «Степень доверия») — это параметр, который означает, какова вероятность,
что верная гипотеза не будет принята. Этот параметр может быть получен, а может быть заранее задан условием, привожу два примера:
- Можем ли мы быть уверены на 90% (уровень значимости 10%), что машину не надо будет сдавать в ремонт в течение года? После проверки гипотезы мы получим результат «да» или «нет»
- На сколько мы можем быть уверены, что машину в течение года не надо будет сдавать в ремонт? После проверки гипотезы мы получим результат в процентах
Ошибки гипотезы
Когда мы делаем утверждение относительно некой гипотезы, мы можем допустить две ошибки:
Ошибка первого рода α
Например, мы провели тест некой выборки и по результатам решили, что параметр X не соответствует генеральной совокупности. Если выборка была
сделана некорректно и параметр X описывает генеральную совокупность, то мы совершили ошибку первого рода — отказались от главной гипотезы
когда она верна.
α = P(ошибка первого рода) = P(отказ от H0 | H0 верна)
Ошибка первого рода и уровень значимости это абсолютно одно и то же.
Пример
Мы взвесили 10 кроликов, их средний вес — 5.1±0.5 кг.
Предположим, что вес кролика подчиняется нормальному закону, тогда:
σ = 0.5/√(10) = 0.16
μ = 5.1
Условие гипотезы:
α = P(H0 неверна | H0 верна) = P(x < )
Ошибка второго рода β
Обратный случай ошибке первого рода — это когда мы приняли главную гипотезу, но она оказалась неверна
β = P(ошибка второго рода) = P(принятие H0 | H0 ошибочна)
Проверка статистической гипотезы
Проверка статистической гипотезы обозначает выполнение следующих шагов:
1. Построение случайной выборки
2. Расчёт параметра X выборки
3. Проверика гипотезы с использованием полученного значения X
Основные принципы и гипотезы сопротивления материалов
Гипотеза
о сплошности:
материал тела представляет собой
однородную сплошную среду.
Гипотеза
об однородности свойств во всех точках
твердого тела:свойства материала
в любой точке одинаковы.
Гипотеза
об изоэнтропности:свойства материала
не меняются от выбранного направления.
Гипотеза
о малости деформаций:деформация
под действием приложенных усилий не
влияет на расчеты усилий в силу их
малости.
Гипотеза
об абсолютной упругости материала:упругие деформации, возникающие под
действием приложенных усилий, полностью
исчезают после прекращения действия
внешних усилий.
Гипотеза
о линейной зависимости между нагрузками
и деформациями:
Принцип
независимости действия сил:порядок
приложения нескольких нагрузок не
влияет на конечный результат.
Принцип
Сен-Венана:в точках тела,
достаточно удалённых от места приложения
нагрузок, внутренние силы весьма
мало зависят от конкретного способа
приложения этих нагрузок. Этот принцип
позволяет производить замену одной
системы сил другой системой, статически
эквивалентной, что может упростить
расчёт.
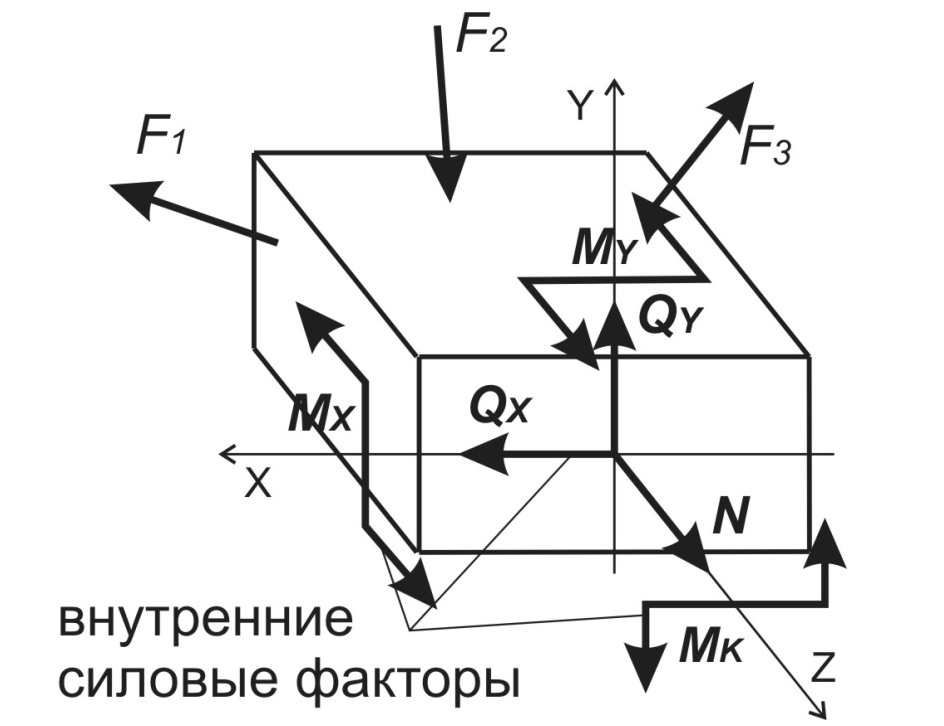
Метод сечений
Метод сечений
(метод РОЗУ) — основной метод
сопротивления материалов, которым
определяют внутренние силовых факторы.
Порядок
расчета:
Рассекаем
тело поперечным сечением

Отбрасываем
любую часть тела. Предпочтительней
оставлять ту часть тела, на которую
действует меньше внешних усилий.
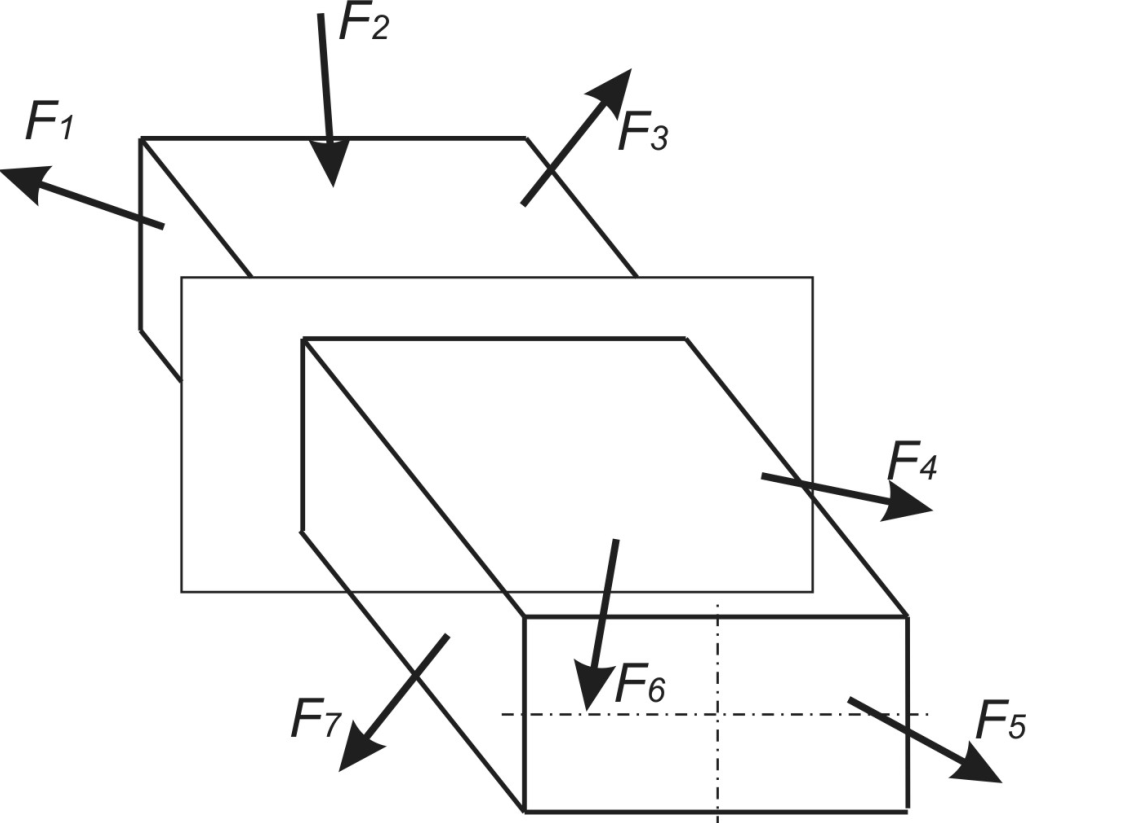
Заменяем
внутренние силы внутренними силовыми
факторами, которые прикладываем к
центру тяжести сечения. На рисунке
моменты MX
MY,
MK
смещены от центра
тяжести сечения для удобства их
восприятия.
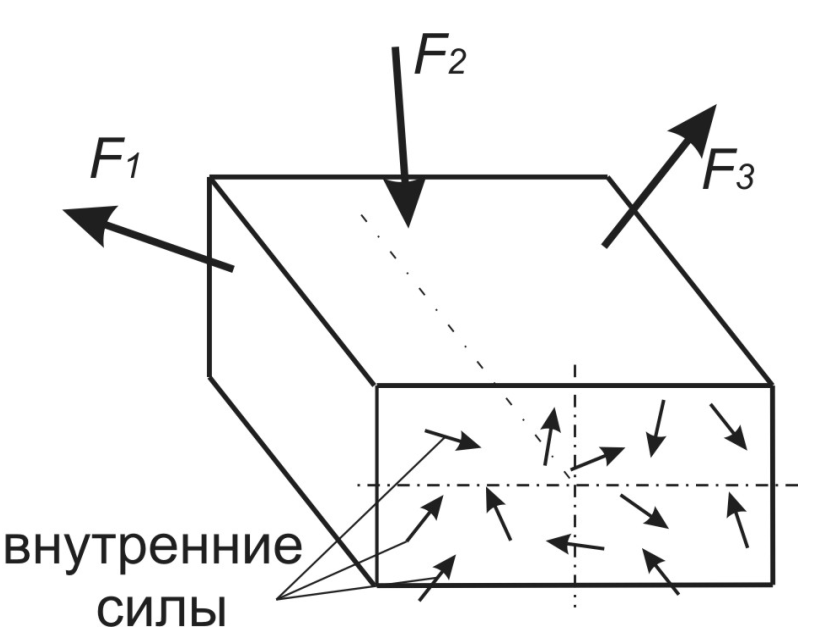
Уравновешиваем
внешние нагрузки и внутренние силовые
факторы, т.е. из уравнений равновесия
выражаем внутренние усилия.
 ,
,
где
Nx- продольное усилие
QyQz–
поперечное усилие
Мх крутящий момент
MyMz–
изгибающие моменты
Условие статического равновесия:
Qy=Qz=Mx=My=Mz=Nx=0
Построение эпюр внутренних силовых факторов
Растяжение-сжатие
Растяжение
(сжатие) — деформация, вызванная
силами или системами сил, равнодействующая
которых или сами силы приложены в центре
тяжести сечения и перпендикулярны
сечению. При растяжении (сжатии) в каждом
сечении бруса действует толькоодин
внутренний силовой фактор — продольная
силаN.
Продольная
сила представляет собой равнодействующую
внутренних нормальных напряжений,
возникающих в поперечном сечении бруса,
численно равную алгебраической сумме
проекций на продольную ось всех внешних
сил, приложенных по одну сторону от
рассматриваемого сечения, т. е.
1.Определяем
реакцию в заделке. Предварительно
произвольно направляем реакцию R.
2.Разбиваем
брус на n участков. Задание координаты
сечения на участке однозначно определяет,
с какой стороны от сечения суммировать
внешние силы при определении внутреннего
силового фактора. Если начало координат
находится снизу (или слева — при
горизонтальном направлении продольной
оси бруса), то рассматриваются все
внешние нагрузки, лежащие снизу (или
слева) от сечения, и наоборот.
3.Составляем
уравнения для продольной силы по
участкам. Согласно методу сечений,
продольная сила равна сумме всех внешних
нагрузок, лежащих по одну сторону (ниже)
от сечения.
4.По
полученным уравнениям строят эпюру
продольных сил.
определение гипотез по The Free Dictionary
Таким образом: — Есть два подразделения, в нижнем или в котором душа использует фигуры, данные в предыдущем разделе, как образы; исследование может быть только гипотетическим, и вместо того, чтобы идти вверх к принципу, спускается к другому концу; в высшем из двух душ переходит от гипотез и подходит к принципу, стоящему над гипотезами, не используя образы, как в первом случае, но действуя только внутри самих идей и через них.
Вам известно, что изучающие геометрию, арифметику и родственные науки предполагают нечетное и четное, и числа, и три вида углов, и тому подобное в своих различных областях науки; это их гипотезы, которые они и все должны знать, и поэтому они не снисходят до того, чтобы давать какой-либо отчет о них ни себе, ни другим; но они начинают с них и продолжаются до тех пор, пока не придут, наконец, и последовательно, к своему заключению?
И об этом я говорил как разумный, хотя в поисках этого душа вынуждена использовать гипотезы; не восхождение к первому принципу, потому что она неспособна подняться над областью гипотезы, но использование объектов, тени которых внизу являются подобиями, в свою очередь, в качестве образов, которые имеют по отношению к теням и отражениям большую четкость , и, следовательно, более высокое значение.
И когда я говорю о другом подразделении умопостигаемого, вы поймете, что я говорю о том другом виде знания, которое сам разум достигает с помощью диалектики, используя гипотезы не как первые принципы, а только как гипотезы — иными словами, как шаги и отправные точки в мир, который выше гипотез, чтобы она могла взлететь за их пределы, к первому принципу целого; и цепляясь за это, а затем за то, что зависит от этого, она последовательно спускается вниз без помощи какого-либо чувственного объекта, от идей через идеи и в идеях она заканчивает.
Я понимаю вас, — ответил он; не идеально, поскольку мне кажется, что вы описываете действительно грандиозную задачу; но, во всяком случае, я понимаю, что вы говорите, что знание и бытие, которые рассматривает диалектическая наука, яснее, чем понятия искусств, как их называют, которые исходят только из гипотез: они также рассматриваются рассудком. и не чувствами: тем не менее, поскольку они исходят из гипотез и не поднимаются до принципа, те, кто их рассматривает, кажется, не применяют к ним высший разум, хотя, когда к ним добавляется первый принцип, они становятся познаваемыми. по высшей причине.
Нетрудно заметить, сколько пустых гипотез и праздных рассуждений поставили человечество на счет явления этой реки.
Но это открытие было зарезервировано для непобедимой храбрости наших благородных соотечественников, которые, не обескураженные опасностями судоходства по морям, никогда ранее не исследовавшимся, покорили царства и империи, где греческое и римское величие, где имена Цезаря и Александр, о которых никогда не слышали; которые разрушили воздушную ткань известных гипотез и обнаружили те басни, которые древние предпочли выдумать об источниках Нила, чем признать свое невежество.
.Журнал изменений
— документация по гипотезе 5.27.0
Гипотеза
последний
- Краткое руководство
- Подробная информация и дополнительные функции
- Настройки
- Что можно производить и как
- Собственные расширения
- Тесты Ghostwriting для вас
- Гипотеза для пользователей Django
- Гипотеза для научного стека
- Проверки здоровья
- База данных примеров гипотез
- Stateful-тестирование
- Совместимость
- Еще несколько примеров
- Сообщество
- Цель гипотезы
- Отзывы
- проектов с открытым исходным кодом, использующих гипотезу
- Проекты, расширяющие гипотезу
- История изменений
- Гипотеза 5.х
- 5.27.0 — 2020-08-20
- 5.26.1 — 2020-08-19
- 5.26.0 — 2020-08-17
- 5.25.0 — 16.08.2020
- 5.24.4 — 14.08.2020
- 5.24.3 — 13.08.2020
- 5.24.2 — 2020-08-12
- 5.24.1 — 12.08.2020
- 5.24.0 — 10.08.2020
- 5.23.12 — 2020-08-10
- 5.23.11 — 2020-08-04
- 5.23.10 — 2020-08-04
- 5.23.9 — 2020-08-03
- 5.23.8 — 2020-07-31
- 5.23.7 - 2020-07-29
- 5.23.6 — 2020-07-29
- 5.23.5 — 2020-07-29
- 5.23.4 — 2020-07-29
- 5.23.3 — 2020-07-27
- 5.23.2 — 2020-07-27
- 5.23.1 — 2020-07-26
- 5.23.0 — 2020-07-26
- 5.22.0 — 2020-07-25
- 5.21.0 — 2020-07-23
- 5.20.4 — 2020-07-23
- 5.20.3 — 2020-07-21
- 5.20.2 — 2020-07-18
- 5.20.1 — 2020-07-17
- 5.20.0 — 2020-07-17
- 5.19.3 — 2020-07-15
- 5.19.2 — 13.07.2020
- 5.19.1 — 2020-07-12
- 5.19.0 — 2020-06-30
- 5.18.3 — 2020-06-27
- 5.18.2 — 2020-06-26
- 5.18.1 — 2020-06-25
- 5.18.0 — 2020-06-22
- 5.17.0 — 2020-06-22
- 5.16.3 — 2020-06-21
- 5.16.2 — 2020-06-19
- 5.16.1 — 2020-06-10
- 5.16.0 — 2020-05-27
- 5.15.1 — 2020-05-21
- 5.15.0 — 2020-05-19
- 5.14.0 — 2020-05-13
- 5.13.1 — 2020-05-13
- 5.13.0 — 2020-05-12
- 5.12.2 — 2020-05-12
- 5.12.1 — 2020-05-12
- 5.12.0 — 2020-05-10
- 5.11.0 — 2020-05-07
- 5.10.5 — 2020-05-04
- 5.10.4 — 2020-04-24
- 5.10.3 — 2020-04-22
- 5.10.2 — 2020-04-22
- 5.10.1 — 2020-04-19
- 5.10.0 — 18.04.2020
- 5.9.1 — 2020-04-16
- 5.9.0 — 2020-04-15
- 5.8.6 — 2020-04-15
- 5.8.5 — 2020-04-15
- 5.8.4 — 2020-04-14
- 5.8.3 — 2020-04-12
- 5.8.2 — 2020-04-12
- 5.8.1 — 2020-04-12
- 5.8.0 — 2020-03-24
- 5.7.2 — 2020-03-24
- 5.7.1 — 2020-03-23
- 5.7.0 — 2020-03-19
- 5.6.1 — 18.03.2020
- 5.6.0 — 2020-02-29
- 5.5.5 — 2020-02-29
- 5.5.4 — 2020-02-16
- 5.5.3 — 2020-02-14
- 5.5.2 — 13.02.2020
- 5.5.1 — 07.02.2020
- 5.5.0 — 07.02.2020
- 5.4.2 — 2020-02-06
- 5.4.1 — 2020-02-01
- 5.4.0 — 2020-01-30
- 5.3.1 — 2020-01-26
- 5.3.0 — 2020-01-21
- 5.2.1 — 2020-01-21
- 5.2.0 — 2020-01-19
- 5.1.6 — 2020-01-19
- 5.1.5 — 2020-01-12
- 5.1.4 — 2020-01-11
- 5.1.3 — 2020-01-11
- 5.1.2 — 2020-01-09
- 5.1.1 — 2020-01-06
- 5.1.0 — 2020-01-03
- 5.0.1 — 2020-01-01
- 5.0.0 — 2020-01-01
- Стратегии
- Разное
- Удаление
- Гипотеза 4.x
- 4.57.1 - 29.12.2019
- 4.57.0 — 28.12.2019
- 4.56.3 — 22.12.2019
- 4.56.2 — 21.12.2019
- 4.56.1 — 19.12.2019
- 4.56.0 — 18.12.2019
- 4.55.4 — 18.12.2019
- 4.55.3 — 18.12.2019
- 4.55.2 — 17.12.2019
- 4.55.1 — 16.12.2019
- 4.55.0 — 16.12.2019
- 4.54.2 — 16.12.2019
- 4.54.1 — 16.12.2019
- 4.54.0 — 15.12.2019
- 4.53.3 — 15.12.2019
- 4.53.2 — 11.12.2019
- 4.53.1 — 09.12.2019
- 4.53.0 — 09.12.2019
- 4.52.0 — 09.12.2019
- 4.51.1 — 09.12.2019
- 4.51.0 — 07.12.2019
- 4.50.8 — 05.12.2019
- 4.50.7 — 05.12.2019
- 4.50.6 — 02.12.2019
- 4.50.5 — 2019-12-01
- 4.50.4 — 01.12.2019
- 4.50.3 — 2019-12-01
- 4.50.2 — 2019-11-29
- 4.50.1 — 2019-11-29
- 4.50.0 — 28.11.2019
- 4.49.0 — 28.11.2019
- 4.48.1 — 28.11.2019
- 4.48.0 — 28.11.2019
- 4.47.5 — 28.11.2019
- 4.47.4 — 27.11.2019
- Гипотеза 5.х
.

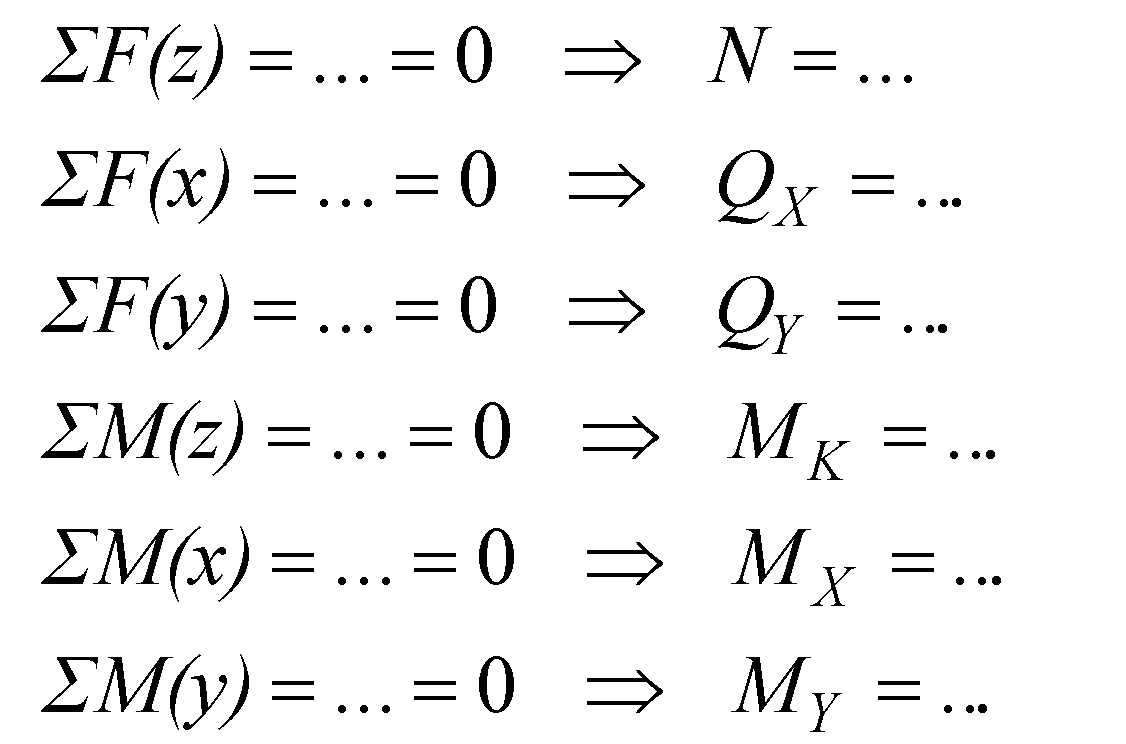 ,
,