Проба Поппельрейтера — Википедия. Что такое Проба Поппельрейтера
Материал из Википедии — свободной энциклопедии
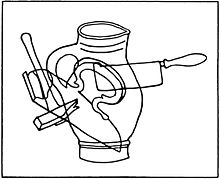Пример фигур Поппельрейтера
Проба Поппельрейтера — нейропсихологическая методика для выявления зрительной агнозии.
Создание методики
Методика была разработана немецким психологом и неврологом Вальтером Поппельрейтером[en] в 1917 году для работы с военными, получившими черепно-мозговые травмы во время Первой мировой войны.[1]
Описание и локализация исследуемого нарушения
Нарушение зрительного гнозиса, а именно предметная агнозия — невозможность правильного распознавания предмета при правильном детальном опознании, локализуется во вторичных 18 и 19 полях правого и левого полушарий головного мозга. Проявляется в замедленной идентификации, фрагментарности, ложном узнавании предмета.
Методика
Проба Поппельрейтера направлена на распознавание контурных, перечеркнутых, наложенных друг на друга, перевёрнутых изображений. При совмещении 3, 4, 5 контуров здоровый видит контуры всех объектов, больной — путаницу линий[2]. Зрительное восприятие предмета затрудняется необходимостью абстрагироваться от посторонних элементов, каждый из которых сам может идентифицироваться как предмет. Инструкция свободная, обычно звучит следующим образом: «Сейчас вы увидите контуры предметов, которые наложены друг на друга. Здесь специально нарисовали предметы, чтобы они налезали один на другой, и Ваша задача разобраться какие предметы вы видите». Считается, что при оптимальном выполнении испытуемый должен начинать опознание группы фигур с самой большой фигуры, а также испытуемому не следует переходить к опознанию фигур другой группы, если опознание предыдущей не завершено.[3]
Достоинства и недостатки методики
Проба Поппельрейтера активно используется в настоящее время и является одной из самых валидных методик для решения топико-диагностических задач диагностики зрительных нарушений. Недостатком в применении этой пробы могут стать когнитивные нарушения, слабое зрение, качество предъявляемых стимулов, что должно быть учтено нейропсихологом для корректной классификации нарушения.
Дальнейшее развитие методики
Помимо классического применения для выявления зрительных агнозий в нейропсихологической диагностике, проба Поппельрейтера используется также для диагностики деменции.[4]
Примечания
См. также
Ссылки
- http://www.sciencedirect.com/science/article/pii/088761779400049V
- https://books.google.ru/books?id=ZS049u1S-yQC&pg=PA48&redir_esc=y#v=onepage&q&f=false
Проба Поппельрейтера — Википедия. Что такое Проба Поппельрейтера
Материал из Википедии — свободной энциклопедии
Пример фигур Поппельрейтера
Проба Поппельрейтера — нейропсихологическая методика для выявления зрительной агнозии.
Создание методики
Методика была разработана немецким психологом и неврологом Вальтером Поппельрейтером[en] в 1917 году для работы с военными, получившими черепно-мозговые травмы во время Первой мировой войны.[1]
Описание и локализация исследуемого нарушения
Нарушение зрительного гнозиса, а именно предметная агнозия — невозможность правильного распознавания предмета при правильном детальном опознании, локализуется во вторичных 18 и 19 полях правого и левого полушарий головного мозга. Проявляется в замедленной идентификации, фрагментарности, ложном узнавании предмета.
Методика
Проба Поппельрейтера направлена на распознавание контурных, перечеркнутых, наложенных друг на друга, перевёрнутых изображений. При совмещении 3, 4, 5 контуров здоровый видит контуры всех объектов, больной — путаницу линий[2]. Зрительное восприятие предмета затрудняется необходимостью абстрагироваться от посторонних элементов, каждый из которых сам может идентифицироваться как предмет. Инструкция свободная, обычно звучит следующим образом: «Сейчас вы увидите контуры предметов, которые наложены друг на друга. Здесь специально нарисовали предметы, чтобы они налезали один на другой, и Ваша задача разобраться какие предметы вы видите». Считается, что при оптимальном выполнении испытуемый должен начинать опознание группы фигур с самой большой фигуры, а также испытуемому не следует переходить к опознанию фигур другой группы, если опознание предыдущей не завершено.[3]
Достоинства и недостатки методики
Проба Поппельрейтера активно используется в настоящее время и является одной из самых валидных методик для решения топико-диагностических задач диагностики зрительных нарушений. Недостатком в применении этой пробы могут стать когнитивные нарушения, слабое зрение, качество предъявляемых стимулов, что должно быть учтено нейропсихологом для корректной классификации нарушения.
Дальнейшее развитие методики
Помимо классического применения для выявления зрительных агнозий в нейропсихологической диагностике, проба Поппельрейтера используется также для диагностики деменции.[4]
Примечания
См. также
Ссылки
- http://www.sciencedirect.com/science/article/pii/088761779400049V
- https://books.google.ru/books?id=ZS049u1S-yQC&pg=PA48&redir_esc=y#v=onepage&q&f=false
Фигуры Поппельрейтера Википедия
Пример фигур Поппельрейтера
Проба Поппельрейтера — нейропсихологическая методика для выявления зрительной агнозии.
Создание методики[ | ]
Методика была разработана немецким психологом и неврологом Вальтером Поппельрейтером[en] в 1917 году для работы с военными, получившими черепно-мозговые травмы во время Первой мировой войны.[1]
Описание и локализация исследуемого нарушения[ | ]
Нарушение зрительного гнозиса, а именно предметная агнозия — невозможность правильного распознавания предмета при правильном детальном опознании, локализуется во вторичных 18 и 19 полях правого и левого полушарий головного мозга. Проявляется в замедленной идентификации, фрагментарности, ложном узнавании предмета.
Методика[ | ]
Проба Поппельрейтера направлена на распознавание контурных, перечеркнутых, наложенных друг на друга, перевёрнутых изображений. При совмещении 3, 4, 5 контуров здоровый видит контуры всех объектов, больной — путаницу линий[2]. Зрительное восприятие предмета затрудняется необходимостью абстрагироваться от посторонних элементов, каждый из которых сам может идентифицироваться как предмет. Инструкция свободная, обычно звучит следующим образом: «Сейчас вы увидите контуры предметов, которые наложены друг на друга. Здесь специально нарисовали предметы, чтобы они налезали один на другой, и Ваша задача разобраться, какие предметы вы видите». Считается, что при оптимальном выполнении испытуемый должен начинать опознание группы фигур с самой большой фигуры, а также испытуемому не следует переходить к опознанию фигур другой группы, если опознание предыдущей не завершено.[3]
Достоинства и недостатки методики[ | ]
Проба Поппельрейтера активно используется в настоящее время и является одной из самых валидных методик для решения топико-диагностических задач диагностики зрительных нарушений. Недостатком в применении этой пробы могут стать когнитивные нарушения, слабое зрение, качество предъявляемых стимулов, что должно быть учтено нейропсихологом для корректной классификации нарушения.
Дальнейшее развитие методики[ | ]
Помимо классического применения для выявления зрительных агнозий в нейропсихологической диагностике, проба Поппельрейтера используется также для диагностики деменции.[4]
Примечания[
Проба Поппельрейтера Википедия
Пример фигур Поппельрейтера
Проба Поппельрейтера — нейропсихологическая методика для выявления зрительной агнозии.
Создание методики[ | ]
Методика была разработана немецким психологом и неврологом Вальтером Поппельрейтером[en] в 1917 году для работы с военными, получившими черепно-мозговые травмы во время Первой мировой войны.[1]
Описание и локализация исследуемого нарушения[ | ]
Нарушение зрительного гнозиса, а именно предметная агнозия — невозможность правильного распознавания предмета при правильном детальном опознании, локализуется во вторичных 18 и 19 полях правого и левого полушарий головного мозга. Проявляется в замедленной идентификации, фрагментарности, ложном узнавании предмета.
Методика[ | ]
Проба Поппельрейтера направлена на распознавание контурных, перечеркнутых, наложенных друг на друга, перевёрнутых изображений. При совмещении 3, 4, 5 контуров здоровый видит контуры всех объектов, больной — путаницу линий[2]. Зрительное восприятие предмета затрудняется необходимостью абстрагироваться от посторонних элементов, каждый из которых сам может идентифицироваться как предмет. Инструкция свободная, обычно звучит следующим образом: «Сейчас вы увидите контуры предметов, которые наложены друг на друга. Здесь специально нарисовали предметы, чтобы они налезали один на другой, и Ваша задача разобраться, какие предметы вы видите». Считается, что при оптимальном выполнении испытуемый должен начинать опознание группы фигур с самой большой фигуры, а также испытуемому не следует переходить к опознанию фигур другой группы, если опознание предыдущей не завершено.[3]
Достоинства и недостатки методики[ | ]
Проба Поппельрейтера активно используется в настоящее время и является одной из самых валидных методик для решения топико-диагностических задач диагностики зрительных нарушений. Недостатком в применении этой пробы могут стать когнитивные нарушения, слабое зрение, качество предъявляемых стимулов, что должно быть учтено нейропсихологом для корректной классификации нарушения.
Дальнейшее развитие методики[ | ]
Помимо классического применения для выявления зрительных агнозий в нейропсихологической диагностике, проба Поппельрейтера используется также для диагностики деменции.[4]
Примечания[
Проба Поппельрейтера Википедия
Пример фигур Поппельрейтера
Проба Поппельрейтера — нейропсихологическая методика для выявления зрительной агнозии.
Создание методики
Методика была разработана немецким психологом и неврологом Вальтером Поппельрейтером[en] в 1917 году для работы с военными, получившими черепно-мозговые травмы во время Первой мировой войны.[1]
Описание и локализация исследуемого нарушения
Нарушение зрительного гнозиса, а именно предметная агнозия — невозможность правильного распознавания предмета при правильном детальном опознании, локализуется во вторичных 18 и 19 полях правого и левого полушарий головного мозга. Проявляется в замедленной идентификации, фрагментарности, ложном узнавании предмета.
Методика
Проба Поппельрейтера направлена на распознавание контурных, перечеркнутых, наложенных друг на друга, перевёрнутых изображений. При совмещении 3, 4, 5 контуров здоровый видит контуры всех объектов, больной — путаницу линий[2]. Зрительное восприятие предмета затрудняется необходимостью абстрагироваться от посторонних элементов, каждый из которых сам может идентифицироваться как предмет. Инструкция свободная, обычно звучит следующим образом: «Сейчас вы увидите контуры предметов, которые наложены друг на друга. Здесь специально нарисовали предметы, чтобы они налезали один на другой, и Ваша задача разобраться, какие предметы вы видите». Считается, что при оптимальном выполнении испытуемый должен начинать опознание группы фигур с самой большой фигуры, а также испытуемому не следует переходить к опознанию фигур другой группы, если опознание предыдущей не завершено.[3]
Достоинства и недостатки методики
Проба Поппельрейтера активно используется в настоящее время и является одной из самых валидных методик для решения топико-диагностических задач диагностики зрительных нарушений. Недостатком в применении этой пробы могут стать когнитивные нарушения, слабое зрение, качество предъявляемых стимулов, что должно быть учтено нейропсихологом для корректной классификации нарушения.
Дальнейшее развитие методики
Помимо классического применения для выявления зрительных агнозий в нейропсихологической диагностике, проба Поппельрейтера используется также для диагностики деменции.[4]
Примечания
См. также
Проба Поппельрейтера — Википедия
Материал из Википедии — свободной энциклопедии
Пример фигур Поппельрейтера
Проба Поппельрейтера — нейропсихологическая методика для выявления зрительной агнозии.
Создание методики
Методика была разработана немецким психологом и неврологом Вальтером Поппельрейтером[en] в 1917 году для работы с военными, получившими черепно-мозговые травмы во время Первой мировой войны.[1]
Описание и локализация исследуемого нарушения
Нарушение зрительного гнозиса, а именно предметная агнозия — невозможность правильного распознавания предмета при правильном детальном опознании, локализуется во вторичных 18 и 19 полях правого и левого полушарий головного мозга. Проявляется в замедленной идентификации, фрагментарности, ложном узнавании предмета.
Методика
Проба Поппельрейтера направлена на распознавание контурных, перечеркнутых, наложенных друг на друга, перевёрнутых изображений. При совмещении 3, 4, 5 контуров здоровый видит контуры всех объектов, больной — путаницу линий[2]. Зрительное восприятие предмета затрудняется необходимостью абстрагироваться от посторонних элементов, каждый из которых сам может идентифицироваться как предмет. Инструкция свободная, обычно звучит следующим образом: «Сейчас вы увидите контуры предметов, которые наложены друг на друга. Здесь специально нарисовали предметы, чтобы они налезали один на другой, и Ваша задача разобраться какие предметы вы видите». Считается, что при оптимальном выполнении испытуемый должен начинать опознание группы фигур с самой большой фигуры, а также испытуемому не следует переходить к опознанию фигур другой группы, если опознание предыдущей не завершено.[3]
Достоинства и недостатки методики
Проба Поппельрейтера активно используется в настоящее время и является одной из самых валидных методик для решения топико-диагностических задач диагностики зрительных нарушений. Недостатком в применении этой пробы могут стать когнитивные нарушения, слабое зрение, качество предъявляемых стимулов, что должно быть учтено нейропсихологом для корректной классификации нарушения.
Дальнейшее развитие методики
Помимо классического применения для выявления зрительных агнозий в нейропсихологической диагностике, проба Поппельрейтера используется также для диагностики деменции.[4]
Примечания
См. также
Ссылки
- http://www.sciencedirect.com/science/article/pii/088761779400049V
- https://books.google.ru/books?id=ZS049u1S-yQC&pg=PA48&redir_esc=y#v=onepage&q&f=false
.
Практические инструменты для художников — линия действий
- +
Учиться
Оздоровительная техника
Более глубокое понимание анатомии
Сокурсники
Другие источники - +
ПривлечьРисунок исследования
животные
Лица и выражение
Руки и ноги
Сцены и окружение - +
обсуждатьрецензия
Практика и советы
Обсуждение магазина
Поддержка и предложения
Учебные группы
Правила сообщества - Новости сайта
- +
хранитьЧленство
Получить больше фото
Подарочные карты
Книги и другие ресурсы - +
Вопросы-ОтветыОтправка фотографий
- Авторизоваться
- регистр
,
Точность, Точность, Отзыв или F1? | Ку Пинг Шунг
Какие метрики выбрать? 
Часто, когда я разговариваю с организациями, которые стремятся внедрить науку о данных в свои процессы, они часто задают вопрос: «Как получить наиболее точную модель?». И я спросил далее: «Какую бизнес-задачу вы пытаетесь решить с помощью этой модели?» и я получу озадаченный взгляд, потому что вопрос, который я задал, на самом деле не отвечает на их вопрос. Затем мне нужно будет объяснить, почему я задал этот вопрос, прежде чем мы начнем исследовать, является ли точность общей метрикой модели, из которой мы выберем нашу «лучшую» модель.
Итак, я подумал, что объясню в этом сообщении в блоге, что точность не обязательно должна быть единственной метрикой модели, которую преследуют ученые, а также включать простое объяснение других метрик.
Во-первых, давайте посмотрим на следующую матрицу путаницы. Какая точность у модели?
Очень легко, вы заметите, что точность для этой модели очень очень высока, 99,9% !! Вот Это Да! Вы сорвали джекпот и Святой Грааль (* кричите и бегайте по комнате, несколько раз взмахнув кулаком *)!
Но….(ну, вы знаете, что все идет правильно?) Что, если бы я упомянул, что положительный момент здесь — это тот, кто болен и несет вирус, который может очень быстро распространяться? Или позитив здесь представляет собой дело о мошенничестве? Или положительный момент здесь представляет террориста, который, согласно модели, не является террористическим? Ну вы поняли. Стоимость ошибочно классифицированного фактического положительного результата (или ложноотрицательного результата) очень высока в этих трех обстоятельствах, которые я назвал.
Хорошо, теперь вы поняли, что точность не является основным показателем модели, который нужно использовать при выборе лучшей модели… что теперь?
Позвольте мне представить две новые метрики (если вы не слышали об этом, а если слышите, возможно, просто развеселите меня и продолжите чтение?: D)
Итак, если вы посмотрите Википедию, вы увидите, что формула для расчета точности и отзыва выглядит следующим образом:
Позвольте мне поместить его здесь для дальнейшего объяснения.
Позвольте мне вставить сюда матрицу путаницы и ее части.
Precision
Отлично! Теперь давайте сначала посмотрим на точность.
Что вы заметили в знаменателе? Знаменатель на самом деле — это общее прогнозируемое положительное значение! Таким образом, формула принимает вид
Истинно Положительный + Ложный Положительный = Всего Прогнозируемый Положительный
Сразу вы можете видеть, что Точность говорит о том, насколько точна / точна ваша модель из предсказанных положительных, сколько из них действительно положительно.
Точность — хороший способ определить, когда цена ложного срабатывания высока. Например, обнаружение спама в электронной почте. При обнаружении спама в электронной почте ложное срабатывание означает, что электронное письмо, не являющееся спамом (фактическое отрицание), было идентифицировано как спам (прогнозируемый спам). Пользователь электронной почты может потерять важные электронные письма, если точность модели обнаружения спама невысока.
Вызов
Итак, давайте применим ту же логику для отзыва. Напомним, как рассчитывается отзыв.
Истинно положительный + ложно отрицательный = Фактический положительный
Вот и все! Таким образом, функция Recall фактически вычисляет, сколько фактических положительных моментов захватывает наша модель, отмечая ее как положительные (истинно положительные). Применяя то же понимание, мы знаем, что Recall будет метрикой модели, которую мы используем для выбора нашей лучшей модели, когда существует высокая стоимость, связанная с False Negative.
Например, при обнаружении мошенничества или выявлении больных. Если мошенническая транзакция (Фактический положительный результат) прогнозируется как не мошенническая (Прогнозируемая отрицательная), последствия могут быть очень тяжелыми для банка.
Аналогично при обнаружении больных. Если больной пациент (Фактический положительный результат) проходит тест и прогнозируется как здоровый (Прогнозируемый отрицательный). Стоимость ложноотрицательного результата будет чрезвычайно высока, если болезнь заразна.
Теперь, если вы читаете много другой литературы по Precision and Recall, вы не сможете избежать другой меры, F1, которая является функцией Precision and Recall. Глядя на Википедию, формула выглядит следующим образом:
F1 Score необходим, когда вы хотите найти баланс между точностью и отзывом.Верно … так в чем же тогда разница между счетом F1 и точностью? Ранее мы видели, что точности может в значительной степени способствовать большое количество истинно отрицательных результатов, на которые в большинстве бизнес-ситуаций мы не обращаем особого внимания, тогда как ложноотрицательные и ложноположительные обычно имеют коммерческие издержки (материальные и нематериальные), поэтому оценка F1 может быть Лучшая мера для использования, если нам нужно найти баланс между точностью и отзывом, И существует неравномерное распределение классов (большое количество фактических отрицательных значений).
Я надеюсь, что объяснение поможет тем, кто только начинает заниматься наукой о данных и работает над проблемами классификации, что точность не всегда будет показателем для выбора лучшей модели.
Примечание: Подпишитесь на мой информационный бюллетень или посетите мой веб-сайт, чтобы узнать последние новости.
Я желаю всем читателям ВЕСЕЛОГО путешествия по науке о данных.
.
Установка размера фигуры с помощью seaborn и matplotlib — рисунок из данных
TL; DR
- , если вы используете
plot ()в pandas Series или Dataframe, используйте ключевое словоfigsize - , если вы используете matplotlib напрямую, используйте
matplotlib.pyplot.figureс ключевым словомfigsize - , если вы используете функцию seaborn, которая рисует один график, используйте
matplotlib.pyplot.figureс ключевым словомfigsize - , если вы используете функцию seaborn, которая рисует несколько графиков, используйте высоту
Введение
Установка размеров фигур, таких как метки с делениями на вращающейся оси, — одна из тех вещей, которые кажутся очень простыми.Однако ему по-прежнему удается отображаться на первой странице вопросов stackoverflow как для matplotlib , так и для seaborn . Отчасти путаница возникает из-за того, что существует множество способов сделать одно и то же — этот вопрос, получивший большое количество голосов, содержит шесть предлагаемых решений:
- вручную создать объект
Axesс желаемым размером - передайте некоторые параметры конфигурации в
seaborn, чтобы желаемый размер был размером по умолчанию - вызывает метод на рисунке после его создания
- передать
hightиаспектключевых слов в функцию построения графикаseaborn - используйте
matplotlib.pyplotи вызовите функциюfigure () - используйте интерфейс
matplotlib.pyplot, чтобы получить текущую цифру, затем установите ее размер с помощью метода
, каждый из которых будет работать в одних обстоятельствах, но не в других!
Рисование фигуры с помощью панд
Давайте перейдем к делу. В качестве примера мы будем использовать набор данных олимпийских медалей, который мы можем загрузить прямо с URL:
импортировать панд как pd
pd.options.display.max_rows = 10
оплаченныйoptions.display.max_columns = 6
data = pd.read_csv ("https://raw.githubusercontent.com/mojones/binders/master/olympics.csv", sep = "\ t")
данные | Город | Год | Спорт | … | Медаль | Страна | Международный код олимпийского комитета | |
|---|---|---|---|---|---|---|---|
| 0 | Афины | 1896 | Водный спорт | … | Золото | Венгрия | HUN |
| 1 | Афины | 1896 | Водный спорт | … | Серебро | Австрия | AUT |
| 2 | Афины | 1896 | Водный спорт | … | бронза | Греция | GRE |
| 3 | Афины | 1896 | Водный спорт | … | Золото | Греция | GRE |
| 4 | Афины | 1896 | Водный спорт | … | Серебро | Греция | GRE |
| … | … | … | … | … | … | … | … |
| 29211 | Пекин | 2008 | Борьба | … | Серебро | Германия | GER |
| 29212 | Пекин | 2008 | Борьба | … | бронза | Литва | LTU |
| 29213 | Пекин | 2008 | Борьба | … | бронза | Армения | РУКА |
| 29214 | Пекин | 2008 | Борьба | … | Золото | Куба | КУБ |
| 29215 | Пекин | 2008 | Борьба | … | Серебро | Россия | РУС |
29216 строк × 12 столбцов
В качестве первого числа мы посчитаем, сколько медалей было выиграно каждой страной, а затем возьмем первую тридцать:
данные ['Страна'].value_counts (). голова (30) США 4335
Советский Союз 2049
Соединенное Королевство 1594
Франция 1314
Италия 1228
...
Испания 377
Швейцария 376
Бразилия 372
Болгария 331
Чехословакия 329
Имя: Country, Length: 30, dtype: int64 И превратить его в гистограмму:
data ['Country']. Value_counts (). Head (30) .plot (kind = 'barh') Игнорируя другие эстетические аспекты сюжета, очевидно, что нам нужно изменить размер, а точнее форму.Отчасти путаница с размерами при построении графиков заключается в том, что иногда нам нужно просто сделать диаграмму больше или меньше , а иногда нам нужно сделать ее на тоньше или толще . Если бы мы просто увеличили этот график так, чтобы он был достаточно большим, чтобы можно было читать имена на вертикальной оси, то он также был бы очень широким. Мы можем установить размер, добавив аргумент ключевого слова figsize в нашу функцию pandas plot () . Значение должно быть набором размеров — на самом деле это горизонтальный и вертикальный размер в дюймах, но для большинства целей мы можем думать о них как о произвольных единицах.
Вот что произойдет, если мы увеличим участок, но сохраним исходную форму:
импортировать matplotlib.pyplot как plt
data ['Country']. value_counts (). head (30) .plot (kind = 'barh', figsize = (20,10)) А вот версия, которая сохраняет большой вертикальный размер, но сжимает диаграмму по горизонтали, чтобы она не занимала так много места:
импортировать matplotlib.pyplot как plt
data ['Country']. value_counts (). head (30) .plot (kind = 'barh', figsize = (6,10)) Рисование фигуры с помощью matplotlib
Хорошо, но что, если мы не используем удобный метод pandas plot () , а рисуем диаграмму напрямую с помощью matplotlib ? Давайте посмотрим, сколько медалей вручается каждый год:
плат.plot (data ['Year']. value_counts (). sort_index ()) На этот раз мы скажем, что хотим сделать график длиннее в горизонтальном направлении, чтобы лучше видеть паттерн во времени. Если мы поищем в документации функцию matplotlib plot () , мы не найдем никаких упоминаний о размере или форме. Это действительно имеет смысл при разработке matplotlib — у графиков действительно нет размера, у фигур есть. Поэтому, чтобы изменить его, мы должны вызвать функцию figure () :
плат.фигура (figsize = (15,4))
plt.plot (данные ['Год']. value_counts (). sort_index ()) Обратите внимание, что с функцией figure () мы должны вызвать ее перед вызовом plot () , иначе она не сработает:
plt.plot (data ['Year']. Value_counts (). Sort_index ())
# нет эффекта, сюжет уже нарисован
plt.figure (figsize = (15,4)) Чертеж фигурки с морскими волнами
Хорошо, а что, если мы используем seaborn, а не matplotlib? Что ж, к счастью, тот же метод будет работать.Из нашего первого графика мы знаем, какие страны выиграли больше всего медалей в целом, но теперь давайте посмотрим, как это зависит от года. Мы создадим сводную таблицу, чтобы показать количество медалей в год для всех стран, которые выиграли не менее 500 медалей.
(не обращайте внимания на эту фигню с пандами, если она кажется запутанной, и просто посмотрите на финальную таблицу)
сводка = (
данные
.groupby ( 'Страна')
.filter (лямбда x: len (x)> 500)
.groupby (['Страна', 'Год'])
.размер()
,to_frame ('количество медалей')
.reset_index ()
)
# перенести длинные названия стран
summary ['Country'] = summary ['Country']. str.replace ('', '\ n')
сводка | Страна | Год | количество медалей | |
|---|---|---|---|
| 0 | Австралия | 1896 | 2 |
| 1 | Австралия | 1900 | 5 |
| 2 | Австралия | 1920 | 6 |
| 3 | Австралия | 1924 | 10 |
| 4 | Австралия | 1928 | 4 |
| … | … | … | … |
| 309 | США \ nStates | 1992 | 224 |
| 310 | США \ nStates | 1996 | 260 |
| 311 | США \ nStates | 2000 | 248 |
| 312 | США \ nStates | 2004 | 264 |
| 313 | США \ nStates | 2008 | 315 |
314 строк × 3 столбца
Теперь мы можем построить коробчатую диаграмму, чтобы показать распределение годовых сумм медалей для каждой страны:
импортировать seaborn as sns
с.н.с..boxplot (
Данные = резюме,
х = «Страна»,
y = 'количество медалей',
цвет = 'красный') Это трудно читать из-за всех названий, поэтому давайте немного их разнесем:
plt. Рисунок (figsize = (20,5))
sns.boxplot (
Данные = резюме,
х = «Страна»,
y = 'количество медалей',
цвет = 'красный') Теперь мы подошли к последнему усложнению; допустим, мы хотим отдельно посмотреть на распределение медалей разных типов. Мы создадим новую сводную таблицу — опять же, не обращайте внимания на информацию о пандах, если она сбивает с толку, и просто посмотрите на итоговую таблицу:
summary_by_medal = (
данные
,GroupBy ( 'Страна')
.filter (лямбда x: len (x)> 500)
.groupby (['Страна', 'Год', 'Медаль'])
.размер()
.to_frame ('количество медалей')
.reset_index ()
)
summary_by_medal ['Страна'] = summary_by_medal ['Страна']. str.replace ('', '\ n')
summary_by_medal | Страна | Год | Медаль | количество медалей | |
|---|---|---|---|---|
| 0 | Австралия | 1896 | Золото | 2 |
| 1 | Австралия | 1900 | бронза | 3 |
| 2 | Австралия | 1900 | Золото | 2 |
| 3 | Австралия | 1920 | бронза | 1 |
| 4 | Австралия | 1920 | Серебро | 5 |
| … | … | … | … | … |
| 881 | США \ nStates | 2004 | Золото | 116 |
| 882 | США \ nStates | 2004 | Серебро | 75 |
| 883 | США \ nStates | 2008 | бронза | 81 |
| 884 | США \ nStates | 2008 | Золото | 125 |
| 885 | США \ nStates | 2008 | Серебро | 109 |
886 строк × 4 столбца
Теперь мы переключимся с boxplot () на более высокий уровень catplot () , так как это упрощает переключение между различными типами графиков.Но обратите внимание, что теперь наш вызов plt.figure () игнорируется:
plt. Рисунок (figsize = (20,5))
sns.catplot (
Данные = summary_by_medal,
х = «Страна»,
y = 'количество медалей',
Оттенок = «Медаль»,
kind = 'box') Причина этого в том, что функции построения графиков более высокого уровня в seaborn (то, что в документации называется Интерфейсы уровня рисунка ) имеют другой способ управления размером, в основном из-за того, что они часто создают несколько подзаголовков.Чтобы установить размер при использовании catplot () или relplot () (также pairplot () , lmplot () и Jointplot () ), используйте ключевое слово height для управления размером и аспект ключевое слово для управления формой:
sns.catplot (
Данные = summary_by_medal,
х = «Страна»,
y = 'количество медалей',
Оттенок = «Медаль»,
Kind = 'окно',
height = 5, # сделать участок высотой 5 единиц
аспект = 3) # высота должна быть в три раза больше ширины Поскольку мы часто заканчиваем рисовать маленькие кратные с помощью catplot () и relplot () , возможность управлять формой отдельно от размера очень удобна.Ключевые слова высота и аспект применяются к каждому подзаголовку в отдельности , а не к фигуре в целом. Поэтому, если мы поместим каждую медаль в отдельный ряд, а не будем использовать оттенок, мы получим три подсюжета, поэтому мы захотим установить меньшую высоту, а соотношение сторон — больше:
sns.catplot (
Данные = summary_by_medal,
х = «Страна»,
y = 'количество медалей',
ROW = 'Медаль',
Kind = 'окно',
высота = 3,
аспект = 4,
color = 'blue') Печать фигуры
Наконец, пару слов о печати.Если причина, по которой вам нужно изменить размер графика, а не форму, заключается в том, что вам нужно его распечатать, не беспокойтесь о размере — получите желаемую форму, затем используйте savefig () сделать сюжет в формате SVG:
plt.savefig ('medals.svg') Это даст вам график в формате масштабируемой векторной графики, в котором хранятся фактические линии и формы диаграммы, так что вы можете распечатать его любого размера — даже гигантский плакат — и он будет выглядеть резким.В качестве приятного бонуса вы также можете редактировать отдельные фрагменты диаграммы с помощью графического редактора SVG (Inkscape является бесплатным и мощным, хотя для его изучения требуется немного усилий).
,